左神算法课程笔记PART2:哈希、布隆过滤器、一致性哈希、并查集、前缀树、贪心、递归和动态规划
文章目录
- 初级班
- lesson5 哈希
- 并查集
- lesson6
- 前缀树
- 贪心
- lesson 7
- 递归和动态规划
初级班
lesson5 哈希
1.细节
推广:如何快速做出1000个哈希函数,且互相独立?
哈希函数结果中每个位置针对于其他位置均独立,可以通过将一个哈希函数的输出按位截取,如截取高八位和低八位,再线性组合的方式即可得到新的哈希函数。线性组合:H+N*L,修改N得到不同独立的新哈希函数,或者将两个独立哈希函数结果线性组合。
哈希函数在大数据中的应用
PS:面试中大数据问题一半都用哈希
需求:我们有一个10TB的大文件存在分布式文件系统上,存的是100亿行字符串,并且字符串无序排列,现在我们要统计该文件中重复的字符串。
整体思路:利用哈希函数分流,以及哈希表的性质:相同输入导致相同输出,不同输入均匀分布。
假设,我们可以调用100台机器来计算该文件。
那么,现在我们需要怎样通过哈希函数来统计重复字符串呢。
首先,我们需要将这一百台机器分别从0-99标好号,然后我们在分布式文件系统中一行行读取文件(多台机器并行读取),通过哈希函数计算hashcode,将计算出的hashcode模以100,根据模出来的值,将该行存入对应的机器中。
根据哈希函数的性质,我们很容易看出,相同的字符串会存入相同的机器中。
然后我们就能并行100台机器,每台机器各自统计有哪些重复的字符串,这样就能大大加加快统计的速度。
如果还嫌单个机器处理的数据过大,可以把机器里的文件再通过哈希函数按照同样的方法把它分成小文件,然后在一台机器中并行多个进程,处理数据。
注意:这10TB文件并不是均分成100GB,分给100台机器,而是将这10TB文件中不同字符串的种类,均分到100台机器中。
2.布隆过滤器
布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都比一般的算法要好的多,缺点是有一定的误识别率和删除困难。
3.一致性哈希
数据存储是根据哈希算法映射到不同服务器。
普通哈希算法缺点:在服务器数量变动时,几乎所有的数据都需要移动(由于模数变动),由此引入一致性哈希。
基本思想:将哈希值绕成了一个环,然后将服务器结合虚拟节点思想放入环中,去争夺所管理的哈希值(两个节点中间部分所有哈希值都属于其顺时针碰到的第一个节点对应的服务器),均分整个环。 不管加机器或者减少机器都是均分,极大减少了增减机器时的需要移动的数据量。
并查集
4.并查集
并查集有两个功能:
1)判断两个元素是否在同一个集合中,
2)根据两个集合中的元素将不是同一集合的整合到一起。
实现步骤:
1)最开始需要将所有的样本点给出
2)首先第一步将所有各自的数目整成一个集合(每个节点单独形成一个集合)
3)在一个集合中每个节点都是自己集合中的代表节点,当集合合并的时候,如果决定将2挂到1的底下,此时2所在集合中,只有1节点指向自己,所以1为这个集合的代表节点。
4)由于每一个集合中都有一个集合的代表节点,所以可以通过代表节点来进行是否在同一个集合的判断,也可以将另外一个集合的代表节点连接到本集合中,此时整个集合也只有一个代表节点,实现集合的整合。(首先进行元素数目的判断,将少元素的集合挂到多元素的底下)
5)在判断两个是否在同一个集合操作时,在向上查找的过程中,将路径上的所有元素直接连接到代表节点上。
【结论】如果查询次数+合并的次数达到O(N)及以上
那么就应该使用并查集结构来做,这样查询过程均摊时间复杂度就是O(1)。
5.岛问题

【思路】两个for循环遍历矩阵,遇到0和2就跳过,遇到1则岛数+1同时进入“感染”函数:将所有和进入位置1沾边的1全部感染成2。
如果矩阵较大,可以分块并行运行上述方法,最后将分开的块进行合并(讨论相邻矩阵边界),从而实现整个题目,其实整个问题已经在上面岛问题的基础上转换成为并查集的题目。
【核心重点】
1)将每一块的岛的数量加起来后,同时只关注边界上的点。
2)每一个岛都用不同标记,比如A、B、C、D。
3)分析两个相邻矩阵相邻的两条边,如果两条边上有岛相邻,则先查看这两个岛(A、B)是否在一个并查集,如果不在,则岛数-1,同时将两岛合并为同一个并查集;如果在一个并查集,则说明之前已经将两岛合并,无需操作。
这样,把一条边界遍历完即可
【注意】这里就非常完美地契合了并查集的结构!
 【思路】
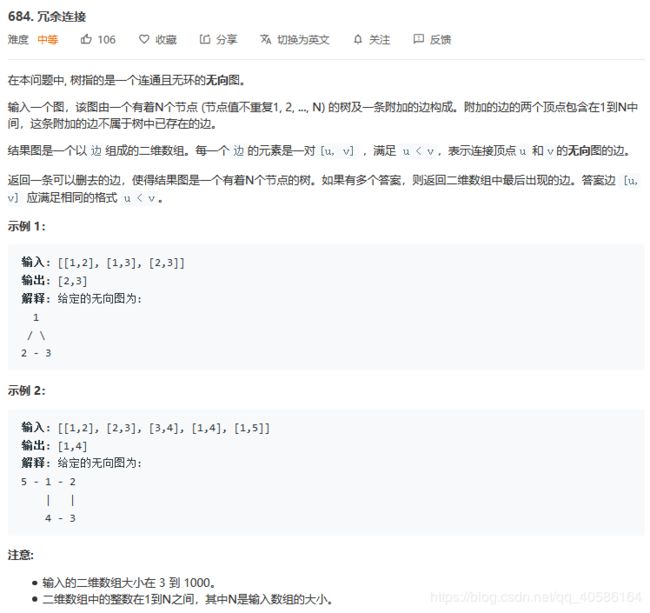
【思路】
1.遍历所有的边edges,将连通的结点放入同一个集合,形成一个联通分量G。
2.在遍历的过程中,如果边(a,b)的两个结点a, b已经属于同一联通分量,则(a,b)就是该联通分量的冗余边。
class Solution {
public:
int parent[1001];//仅使用简单数组功能,普通数组快于动态数组vector
int findRoot(int x){
if(parent[x]!=x){
parent[x]=findroot(parent[x]);//压缩路径
}
return parent[x];
}
bool Unoin(int a,int b){
int a_root=findRoot(a);
int b_root=findRoot(b);
if(a_root==b_root)
return false;
parent[a_root]=b_root;
findRoot(a);//合并完立即压缩路径
return true;
}
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
for(int i=0;i<1001;i++)//先全部初始化,可以充分利用cache,比用到后再初始化快得多
parent[i]=i;
for(auto edge:edges){
if(!Unoin(edge[0],edge[1]))
return {edge[0],edge[1]};
}
return {};
}
};
lesson6
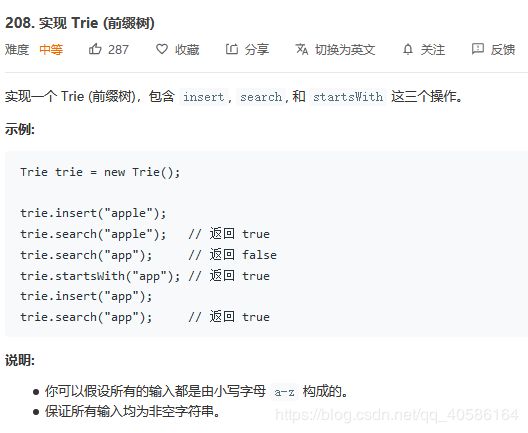
前缀树
又称字典树,Trie树,是一种树形结构,是哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。 注意信息在路上

前缀树用上图进行理解,其中节点均用圆圈表示,“abc”等字符加入到整棵树中作为路径加入,而不是以节点形式加入,同时每个字符在加入时均从头结点出发,因此可以看到“abc”和“bce”为两个分支,同时“abc”和“abd”前半段为一个分支,最后形成两个分支。
扩充功能:
每个节点有两个成员变量path、end
1)path意味着该节点对应的字母被经过的次数(含有该前缀的字符串个数)。
2)end意味着以该字母为结尾的字符串个数(这个字符串被加入了几次)。
public static class TrieNode{
public int path; //有多少个字符串到达过这个节点
public int end; //有多少个字符串以这个节点结尾
public TrieNode[] nexts; //
public TrieNode(){
path = 0;
end = 0;
//这里指的是路,每个题具体分析,这里将26个字母作为26条路
nexts = new TrieNode[26];
}
}
public static class Trie{
private TrieNode root;
public Trie(){
//新建的头,就是整体的头节点
root = new TrieNode();
}
//插入一条字符串
public void insert(String word){
if(word == null){
return;
}
char[] chs = word.toCharArray(); //word转为字符数组,开始跑
TrieNode node = root; //根节点,它的path和end不包含信息
int index = 0;
for(int i =0;i<chs.length;i++){
//用ASCII码和a的差值来表示字母,a--0,b--1,c--2,z--25
index = chs[i] - 'a';
//判断当前节点是否有通向chs[i]这个字母的路
if(node.nexts[index] == null){
node.nexts[index] = new TrieNode(); //没有就新建路
}
node = node.nexts[index];
node.path++;
}
node.end++;
}
//删除
public void delete(String word){
if(search(word) != 0){ //先查有没有
char[] chs = word.toCharArray();
TrieNode node = root;
int index = 0;
for(int i = 0;i<chs.length;i++){
index = chs[i] - 'a';
//路径信息某个节点减一变成0,
//意味着接下来的字符串全部都是所需要删除的字符串,
//所以下面的字符串直接设置为null
if(--node.nexts[index].path == 0){
node.nexts[index] = null;
return;
}
node = node.nexts[index];
}
node.end--;
}
}
//查找一个word在其中出现过几次
public int search(String word){
if(word == null){
return ;
}
char[] chs = word.toCharArray();
TrieNode node = root;
int index = 0;
for(int i = 0;i<chs.length;i++){
index = chs[i] - 'a';
if(node.nexts[index] == null){
return 0; //在任何一步遇到空,说明没插入过
}
node = node.nexts[index];
}
return node.end; //遇到最后返回end
}
public int prefixNumber(String pre){
if(pre == null){
return 0;
}
char[] chs = pre.toCharArray();
TrieNode node = root;
int index = 0;
for(int i = 0;i<chs.length;i++){
index = chs[i] - 'a';
if(node.nexts[index] == null){
return 0;
}
node = node.nexts[index];
}
return node.path;
}
}
struct TrieNode {
shared_ptr<TrieNode> nexts[26];
bool isEnd=false;
};
class Trie {
public:
shared_ptr<TrieNode> root;
/** Initialize your data structure here. */
Trie():root(make_shared<TrieNode>()) {}
/** Inserts a word into the trie. */
void insert(string word) {
shared_ptr<TrieNode> node=root;
for(char i:word){
int index=i-'a';
if(node->nexts[index]==nullptr){
node->nexts[index]=make_shared<TrieNode>();
}
node=node->nexts[index];
}
node->isEnd=true;
}
/** Returns if the word is in the trie. */
bool search(string word) {
shared_ptr<TrieNode> node=root;
for(char i:word){
int index=i-'a';
if(node->nexts[index]==nullptr)
return false;
node=node->nexts[index];
}
return node->isEnd;
}
/** Returns if there is any word in the trie that starts with the given prefix. */
bool startsWith(string prefix) {
shared_ptr<TrieNode> node=root;
for(char i:prefix){
int index=i-'a';
if(node->nexts[index]==nullptr)
return false;
node=node->nexts[index];
}
return true;
}
};
【TIP】Trie类对象离开作用域后自动析构–>root自动析构–>root智能指针指向的TrieNode节点自动析构–>next数组自动析构–>数组中智能指针指向的TrieNode节点自动析构–> …… ,类似于多米诺骨牌,所有子节点全部析构。
【方法二】只有根节点用智能指针,但需要附加析构函数,比起方法一更优,占内存更少:
struct TrieNode {
TrieNode* nexts[26]={NULL};
bool isEnd=false;
~TrieNode(){
for(int i=0;i<26;i++)
delete nexts[i];
}
};
class Trie {
public:
shared_ptr<TrieNode> root;
/** Initialize your data structure here. */
Trie():root(make_shared<TrieNode>()) {}
/** Inserts a word into the trie. */
void insert(string word) {
TrieNode* node=root.get();
for(char i:word){
int index=i-'a';
if(node->nexts[index]==nullptr){
node->nexts[index]=new TrieNode;
}
node=node->nexts[index];
}
node->isEnd=true;
}
/** Returns if the word is in the trie. */
bool search(string word) {
TrieNode* node=root.get();
for(char i:word){
int index=i-'a';
if(node->nexts[index]==nullptr)
return false;
node=node->nexts[index];
}
return node->isEnd;
}
/** Returns if there is any word in the trie that starts with the given prefix. */
bool startsWith(string prefix) {
TrieNode* node=root.get();
for(char i:prefix){
int index=i-'a';
if(node->nexts[index]==nullptr)
return false;
node=node->nexts[index];
}
return true;
}
};
贪心
1.字符串数组最小字典序拼接
【题目】给定一个字符串类型的数组strs,找到一种拼接方式,使得把所有字符串拼起来之后形成的字符串具有最低的字典序。
【思路】按照 str1拼接str2
2.切金条
 贪心策略是:把数组变成小根堆,每次都取堆中最小的,把这两个数的和再加到堆里。重复这样处理的过程,直到最后堆中只剩下1个数为止。(哈夫曼问题)
贪心策略是:把数组变成小根堆,每次都取堆中最小的,把这两个数的和再加到堆里。重复这样处理的过程,直到最后堆中只剩下1个数为止。(哈夫曼问题)
3.项目最大收益

思路:用两个堆:cost小根堆和利润的大根堆。
按照花费的多少放到一个小根堆里面,只要小根堆堆顶的花费少于给定资金,就将头节点一个个取出来,放到按照收益的大根堆里面,然后将大根堆的堆顶弹出。
public static int findMaximizedCapital(int k,int W,int[] Profits,int[] Capital){
Node[] nodes = new Node[Profits.length];
for(int i = 0;i<Profits.length;i++){
nodes[i] = new Node(Profits[i],Capital[i]);
}
//MinCostComparator和下面的Max都是继承比较器,将Node中的cost花费进行比较,实现大根堆和小根堆
PriorityQueue<Node> minCastQ = new PriorityQueue<>(new MinCostComparator());
PriorityQueue<Node> maxProfitQ = new PriorityQueue<>(new MaxProfitComparator());
for(int i = 0;i<nodes.length;i++){
minCostQ.add(nodes[i]);
}
for(int i = 0;i<k;i++){
while(!minCostQ.isEmpty() &&minCostQ.peek().c<=W){
maxProfitQ.add(minCostQ.poll());
}
if(maxProfitQ.isEmpty()){
return W;
}
W += maxProfitQ.poll().p;
}
return W;
}
4.会议安排问题
lesson 7
递归和动态规划
 1.汉诺塔问题
1.汉诺塔问题
打印n层汉诺塔从最左边移动到最右边的全部过程
public static void process(int N,String from,String to,String help){
if(N==1){
System.out.println("move 1 from" + from + " to " + to;
}else{
process(N-1,from,help,to);
System.out.println("move" +N +"from " +from + "to" + to);
process(N-1,help,to,from);
}
}
2.打印字符串子序列,包括空字符串。
子序列:一个字符串 s 被称作另一个字符串 S 的子序列,说明从序列 S 通过去除某些元素但不破坏余下元素的相对位置(在前或在后)可得到序列 s 。
子串:一个字符串 s 被称作另一个字符串 S 的子串,表示 s 在 S 中出现了。
public static void printAllSub(char[] Str,int i,String res){
if(i == str.length){
System.out.println(res);
return;
}
//不要当前字符
printAllSub(str,i+1,res);
//要当前字符
printAllSub(str,i+1,res+String.valueof(str[i]));
}
3.母牛繁衍问题
f(n)=f(n-1)+f(n-3)
进阶:f(n)=f(n-1)+f(n-3)+f(n-10)
4.数组最小路径
给定一个二维数组,二维数组中的每个数都是正数,要求从左上角到右下,每一步只能向右或向下,沿途经过的数字要累加起来,返回最小路径和。
【思路】暴力递归:先考虑右下方最后一格,再考虑到达下边界或右边界的情况,最后考虑一般情况,进行递归。
public static int walk(int[][] matrix,int i,int j){
if(i==matrix.length-1 && j == matrix[0].length-1){
return matrix[i][j];
}
if(i == matrix.length-1){
return matrix[i][j] + walk(matrix,i,j+1);
}
if(j == matrix[0].length-1){
return matrix[i]ij]+ walk(matrix,i+1,j);
}
int right = walk(matrix,i,j+1);//右边位置到右下角的最短路径和
int down = walk(matrix,i+1,j);//下边位置到右下角最短路径和
return matrix[i][j] + Math.min(right,down);
}
改为 动态规划:
对于这道题目,可以按照上述代码,可以首先将最后一行中到右下角的距离挨个计算出,此时为最后一行的点到右下角的距离。也要先将最后一列中到右下角的距离挨个算出,为最后一列的点到右下角的距离。此时可以从右到左,再从下到上,就可以 计算出整个距离。 用一个二维表把整个返回值装下来。
暴力递归改成动态规划的步骤:
1)先写出一个暴力递归(尝试版本)。
2)确定无后效性,列出可变参数(哪几个可变参数可以代表返回值的状态),可变参数几维那就是一张几维的表。
3)确定最终状态。回到baseCase中,将完全不依赖的值设置好。
4)由已知数据和状态转移方程逐步返回,就是填表的顺序。
最后就可以将暴力递归改成动态规划。
无后效性:参数确定,返回值确定。如果在某个阶段上过程的状态已知,则从此阶段以后过程的发展变化仅与此阶段的状态有关,而与过程在此阶段以前的阶段所经历过的状态无关。即“未来与过去无关”。
5.数组与累加和
给定一个数组arr和一个整数aim,如果可以任意选择arr中的数字,能不能累加得到aim,返回true或者false。
【步骤】
第一步: 写出递归的“试”法,看看如何尝试可以解决问题。
思路:设置sum,对于每一个数组中的数字,都可以进行判断,是否要当前的数字,分为两种情况,然后最后和aim相比较。如果发现最后的结果中存在aim,则返回true。
//{3,1,4,2,7}
public static boolean isSum(int[] nums, int i, int sum, int target){
if(i == nums.length-1)
return sum == target;
//这个方法会遍历所有的子集合
return isSum(nums, i+1, sum, target)|| //注意这个||
isSum(nums, i+1, sum+nums[i], target);
}
PS:如果有则返回true,否则返回false,在递归中得使用|| !!
第二步: 判断是否是无后效性问题,分析是否有后效性:之前形成的累加和确定跟之后的数组无关,分析可变参数:i,sum是可变参数,arr和aim确定,所以建立二维表(i,sum)。
第三步:结合暴力版本中i==arr.length,所以i为0~N,起始位置为(0,0)。最后一行中只有sum等于aim上的值时返回true。
第四步:子过程i+1,所以可以从最后一行推出倒数第二行,上一行的位置有sum的位置和sum+arr[i]确定,从而每个位置都可以推出来。
6.递归逆序栈
给你一个栈,请你逆序这个栈,不能申请额外的数据结构,只能使用递归函数。如何实现?
public static void reverse(Stack<Integer> stack) {
if (stack.isEmpty()) {
return;
}
int i = getAndRemoveLastElement(stack);
reverse(stack);
stack.push(i);
}
//将栈底元素移出并返回该元素
public static int getAndRemoveLastElement(Stack<Integer> stack) {
int result = stack.pop();
if (stack.isEmpty()) {
return result;
} else {
int last = getAndRemoveLastElement(stack);
stack.push(result);
return last;
}
}
7.背包问题
给定两个数组w和v,两个数组长度相等,w[i]表示第i件商品的重量,v[i]表示第i件商品的价值。
再给定一个整数bag,要求你挑选商品的重量加起来一定不能超过bag,返回满足这个条件下,你能获得的最大价值。
递归:
public static int process1(int[] c, int[] p, int i, int cost, int bag) {
if (cost > bag) {
return Integer.MIN_VALUE; //超过bag就给系统最小
}
if (i == c.length) {
return 0;
}
return Math.max(process1(c, p, i + 1, cost, bag), p[i] + process1(c, p, i + 1, cost + c[i], bag));
}
dp:
vubliw statiw int maxValue2(int[] w, int[] v, int bag) {
int[][] dp = new int[w.length + 1][bag + 1];
for (int i = w.length - 1; i >= 0; i--) {
for (int j = bag; j >= 0; j--) {
dp[i][j] = dp[i + 1][j];
if (j + w[i] <= bag) {
dp[i][j] = Math.max(dp[i][j], v[i] + dp[i + 1][j + w[i]]);
}
}
}
return dp[0][0];
}