剑指offer(21---30)

21、栈的压入、弹出序列

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。（注意：这两个序列的长度是相等的）

解决这个问题，我们定义两个变量i用来遍历压入序列，j用来遍历弹出序列，例如压入序列pushV：1 2 3 4 5和弹出序列popV：4 5 3 2 1，当栈为空或者栈顶元素不是popV[j]，只要i没有超过压入序列的长度，就将pushV[i]入栈，直到栈顶元素与popV[j]相等，出栈，j向后走，直到将popV全部遍历完，都没有返回false，就返回true（这里要注意如果i超过了pushV的长度，说明此时pushV的所有元素都已经遍历过，已经入过栈了，但是此时栈顶元素不等于PopV[j]，说明不是正确的弹出序列，直接返回false）
例如上述的例子，压入序列1 2 3 4 5，弹出序列4 5 3 2 1，分析如下：

当前j指向4，i指向1，此时栈为空，1入栈，i走向2，此时栈顶元素1与4不相等，2入栈，i走向3，栈顶元素2与4不相等，3入栈，i走向4，栈顶元素3与4不相等，4入栈，i走向5，栈顶元素4与4相等，4出栈，此时j++后指向5，此时栈顶元素3与5不相等，5入栈，i++，此时栈顶元素5与5相等，5出栈，j++后指向3，此时栈顶元素3与3相等，3出栈，j++后指向2，此时栈顶元素2与2相等，2出栈，j++后指向1，此时栈顶元素1与1相等，1出栈，j++此时大于popV的长度，循环结束，返回true；

而分析压入序列1 2 3 4 5和错误的弹出序列4 3 5 1 2，分析如下：

当前j指向4，i指向1，此时栈为空,1入栈，i走向2，此时栈顶元素1与4不相等，2入栈，i走向3，此时栈顶元素2与4不相等，3入栈，i走向4，此时栈顶元素3与4不相等，4入栈，i走向5，此时栈顶元素4与4相等，4出栈，j++后指向3，此时栈顶元素3与2不相等，5入栈，i++后超过pushV的长度，此时栈顶元素5与3不相等，直接返回false。

class Solution {
public:
    bool IsPopOrder(vector pushV,vector popV) {
        std::stack s;
        int i=0;//指向pushV
        int j=0;//指向popV
        //每次看栈顶元素是否和当前popV[j]相同
        while(j

22、从上往下打印二叉树

从上往下打印出二叉树的每个节点，同层节点从左至右打印。

这个题就是将层序遍历的结果插入一个顺序表中，这里利用队列先进先出的特性，先将根结点插入队列，然后循环，将队首元素的值插入顺序表中，再出队，然后如果他有左孩子，插入队列，有有孩子也插入队列，继续循环直到队列为空。

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
    vector PrintFromTopToBottom(TreeNode* root) {
        vector result;
        if(root==nullptr)
            return result;
        std::queue q;//利用队列的先进先出的特性，层序遍历
        q.push(root);
        while(!q.empty())
        {
            root=q.front();//每次取队首元素
            result.push_back(root->val);
            q.pop();
            //然后将这个队首元素的左孩子和右孩子分别入队，继续循环直到队列为空
            if(root->left)
                q.push(root->left);
            if(root->right)
                q.push(root->right);
        }
        return result;
    }
};

23、二叉搜索树的后序遍历序列

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。

这个题目要注意是一棵二叉搜索树，那么它的后序遍历序列最后一个一定是根结点，根结点的左子树的所有节点一定比根结点的值小，右子树的所有节点一定比根结点的值大，因此这里从头遍历给定序列遇到比根结点的值大的就break，然后从break的位置开始遍历，如果还有比根结点的值小的，说明这个序列代表的不是一棵二叉搜索树，直接返回false即可，此时就可以将这个序列分为三部分，即根结点的左子树序列、根结点的右子树序列、根结点，然后根结点的左子树和右子树继续递归看是否满足上述规则（这里要注意的是要判断左子树和右子树是否存在），如果两者递归的结果都为true，说明这最终的结果就是true，否则就返回false；
实现代码：

class Solution {
public:
    bool VerifySquenceOfBST(vector sequence) {
        return _VerifySquenceOfBST(sequence,0,sequence.size()-1);
    }
private:
    bool _VerifySquenceOfBST(vector sequence,int begin,int end)
    {
        if(sequence.empty() || begin>end)
            return false;
        int i=begin;
        for(;isequence[end])
                break;//i就为根结点左右子树的分界点
        }
        for(int j=i;jbegin)//左子树递归,这个条件表示此时有左子树结点
            x=_VerifySquenceOfBST(sequence,begin,i-1);
        if(i

24、二叉树中和为某一值的路径

输入一颗二叉树的根节点和一个整数，按字典序打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。

一条完整的路径指的是从根结点走到没有左孩子才算一条完整的路径，以下图为例分析：

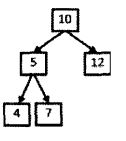
比如我们的值为22，此时走到10，将10尾插到保存路径值的数组tmp中，他还有左孩子，因此不是一条完整的路径，并且10也不是我们要的值22，此时开始递归从10的左孩子5开始，将5尾插到保存路径值的数组tmp中，此时要的值变为22-10=12，但是5也不是要的值12，并且5还有左孩子，因此不是一条完整的路径，又开始递归从5的左孩子4开始，将4尾插到保存路径值的数组tmp中，此时要的值变为12-5=7，但是4也不是要的值7，此时要从4的左孩子递归，此时已经为空，到达递归终止条件，返回到4，此时要将4从这条路径中移出去，也就是判断保存路径值的数组tmp是否不空，不空尾删一个元素，也就将4删除掉了，此时又从5的右孩子7开始递归，将7尾插到tmp中，此时要的值是7，正好是，并且7也没有左孩子，此时就将tmp尾插到最终的结果二维数组buf中；基本后面就是按照这个过程进行实现，这里尤其要知道一条完整的路径是要到没有左孩子的叶节点才可以，并且每走一步，要记得将当前的根结点的值尾插到tmp中，后面递归如果不符合，只需要尾删即可，递归也会自动回溯到当前叶节点的父节点。
实现代码：

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
private:
    //要定义成员变量tmp和buf，因为要递归，但是tmp和buf要保存每一次的结果，递归会将上一次保存的结果给消除掉
    vector tmp;
    vector> buf;
public:
    vector > FindPath(TreeNode* root,int expectNumber) {
        if(root==nullptr)
            return buf;
        tmp.push_back(root->val);//将每一次当前根结点的值尾插到tmp中，
        if(expectNumber-root->val==0 && root->left==nullptr)//到当前结点时与要的值相同并且是一条完整的路径
            buf.push_back(tmp);
        FindPath(root->left, expectNumber-root->val);//走到上一个结点的左孩子，此时expectNumber就要减去上一个结点的值
        FindPath(root->right,expectNumber-root->val);
        if(!tmp.empty())
            //这里考虑的是到了某个叶节点并且这条路径走完了，但是相加结果不是expectNumber
            //就要去掉这个叶节点，也就是tmp的最后一个尾插的值
            //前面的递归也可以回到叶节点的父节点
        {
            tmp.pop_back();
        }
        
        return buf;
    }
};

25、复杂链表的复制

输入一个复杂链表（每个节点中有节点值，以及两个指针，一个指向下一个节点，另一个特殊指针random指向一个随机节点），请对此链表进行深拷贝，并返回拷贝后的头结点。（注意，输出结果中请不要返回参数中的节点引用，否则判题程序会直接返回空）

比如我们有一个链表1–>2–>3–>4,1的random指向2,2的random指向1,3的random指向自己，4的random指向nullptr，这就包含了所有可能的random指向的情况，此时要复制复杂链表，应该做以下：
（1）复制结点，也就是构造和原来值一样的结点，然后将其构成一个表，构造完成为1–>1–>2–>2–>3–>3–>4–>4–>nullptr；
（2）复制random指针，如果当前结点的random域指向nullptr，比如4的情况，此时它的next域结点的random也为nullptr，否则就是1 2 3的情况，也就是当前结点的next域结点的random指向当前结点的random域的next结点；
（3）拆下结点，构造新链表，也就是将新的结点构成链表拆下来即可

/*
struct RandomListNode {
    int label;
    struct RandomListNode *next, *random;
    RandomListNode(int x) :
            label(x), next(NULL), random(NULL) {
    }
};
*/
class Solution {
public:
    RandomListNode* Clone(RandomListNode* pHead)
    {
        if(pHead==nullptr)
            return nullptr;
        RandomListNode* pCur=pHead;
        while(pCur)
        {
            RandomListNode* node=new RandomListNode(pCur->label);
            //开始给每一个结点后插入与自己相同的结点
            node->next=pCur->next;
            pCur->next=node;
            pCur=node->next;//cur向自己原来的链表往后走，这样循环直到pCur为空就将链表的值都复制了一遍
            //例如原链表1234nullptr，则复制过的链表为11223344nullptrnullptr
        }
        //接下来进行random指针的复制
        pCur=pHead;
        while(pCur!=nullptr && pCur->next!=nullptr)
        {
            //先考虑结点的random为空的情况
            if(pCur->random==nullptr)
            {
                pCur->next->random=nullptr;
            }
            else{
                pCur->next->random=pCur->random->next;
            }
            pCur=pCur->next->next;
        }
        //将新链表取出来
        pCur=pHead;
        RandomListNode* pNewNode=pHead->next;//定义新链表
        while(pCur!=nullptr && pCur->next!=nullptr)//将新链表的每个结点拆下来
        {
            RandomListNode* node=pCur->next;
            pCur->next=node->next;
            //拆下来node，将next指针指好
            if(node->next!=nullptr)
            {
                node->next=node->next->next;
            }
            //这里已经将node拆下来了，pCur可以直接走向下一个
            pCur=pCur->next;
        }
        return pNewNode;
        
    }
};

26、字符串的排列

输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。

这个题其实可以分为两步：
（1）固定第一个字符，后面的字符递归进行排列
（2）求所有可能出现在第一个位置的字符，也就是将第一个字符与后面的所有字符交换

class Solution {
vector result;
public:
    vector Permutation(string str) {
        if(str.empty())
            return result;
        Helper(str,0);
        sort(result.begin(),result.end());
        return result;
    }
    void Helper(string str,int begin)//begin指向当前做排列的字符串的第一个
    {
        //递归条件
        if(begin==str.size())//说明以某个字符为首元素的一个排列生成了
        {
            result.push_back(str);
        }
        else{
            for(int i=begin;str[i]!='\0';++i)//用来进行从begin到最后一个元素的排列
            {
                //连续两个元素相同的情况，不用处理，直接下次循环
                if(i!=begin && str[i]==str[begin])
                    continue;
                //第一步，
                swap(str[i],str[begin]);
                Helper(str,begin+1);
                swap(str[i],str[begin]);//与后面的进行交换作为首元素
            }
        }
    }
};

28、数组中出现次数超过一半的数字

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2。如果不存在则输出0。

数组中出现次数超过一半的数字，那么意思就是他出现的次数比其他所有数字出现次数的和还要多，此时就可以将数组分为要找的数字和其他数字，因此遍历数组时，我们可以保存两个值，一个用来保存数组中的一个元素，一个是次数；我们保存当前元素，如果下一个和之前保存的元素相同，次数+1，如果不同，次数-1，如果次数为0，此时就保存下一个数字，将次数设为1，我们要找的数字出现的次数比其他数字出现的次数之和还要多，因此要找的数字肯定是最后一次把次数设为1的数字。最后再遍历一次数组将这个数字的次数统计即可。
实现代码：

class Solution {
public:
    int MoreThanHalfNum_Solution(vector numbers) {
        if(numbers.empty())
            return 0;
        int count=1;//设为1表示此时有第一个数字
        int ret=numbers[0];//先保存第一个数字
        for(int i=1;i(numbers.size())/2 ? ret:0;
    
    }
};

29、最小的k个数

输入n个整数，找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字，则最小的4个数字是1,2,3,4,。

这个有点类似Topk问题，不过这里改成了最小的k个数，我们用前k个元素建一个大堆，然后剩下的元素与堆顶元素相比，如果比他小，就将堆顶元素删除，将它插入，然后调整成堆即可（即先将堆顶元素与最后一个叶子节点交换，然后pop_back删除，然后将这个元素push_back插入，然后调整成堆），最后对这个堆进行排序即可。
实现代码：

class Solution {
public:
    vector GetLeastNumbers_Solution(vector input, int k) {
        vector result;
        if(input.empty() || k==0 || k>input.size())
            return result;
        for(int i=0;i

30、连续子数组的最大和

在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢？例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组，返回它的最大连续子序列的和，你会不会被他忽悠住？(子向量的长度至少是1)

这个题解决思路就是假设和sum为第一个元素，最大值也为第一个元素，遍历数组，如果sum>0，sum加上当前元素，否则sum变为当前元素，然后将sum与maxsum比较得到相对较大的，遍历完得到的maxsum就是最大和。

class Solution {
public:
    int FindGreatestSumOfSubArray(vector array) {
        if(array.empty())
            return 0;
        int sum=array[0];
        int maxsum=sum;
        for(int i=1;i0) ? (sum+array[i]):array[i];
            maxsum=(maxsum>sum) ? maxsum:sum;
        }
        return maxsum;
    }
};