Sarcasm Detection with Self-matching Networks and Low-rank Bilinear Pooling
Sarcasm Detection with Self-matching Networks and Low-rank Bilinear Pooling
click here:文章下载
方法综述:
本文中使用了三个模型,分别是self-matching network、Bi-LSTM、Low-rank Bilinear Pooling method(LBPR):
self-matching network: 通过单词对间的信息,获取句子的incongruity information
Bi-LSTM: 通过句子的序列信息,获取句子的compositional information
Low-rank Bilinear Pooling method: 融合incongruity information和compositional information
各模型算法:
self-matching network
target: 求输入句子的 attend feature vector : f a ∈ R k ⟹ f a = S ⋅ a f_a \in R^k \implies f_a=S·a fa∈Rk⟹fa=S⋅a
S是输入句子的word-embedding表示, S ∈ R k × n S \in R^{k \times n} S∈Rk×n
于是问题转变成为,求解self-matched attention vector : a ∈ R n a \in R^n a∈Rn
其中,k为单词表示维度,n为句子单词数。
求解 a ∈ R n a \in R^n a∈Rn:
考虑到,单词对表示向量间进行内积运算,只抓住特征向量间的相关性,却忽视了情感信息,所以定义了一种新的计算方式。对于单词对 ( e i , e j ) (e_i, e_j) (ei,ej), e i ∈ R k e_i \in R^k ei∈Rk:
joint feature vector: w i , j ∈ R ⟹ w i , j = t a n h ( e i ⋅ M i , j ⋅ e j T ) w_{i,j} \in R \implies w_{i,j}=tanh(e_i · M_{i,j} · e_j^T) wi,j∈R⟹wi,j=tanh(ei⋅Mi,j⋅ejT)
其中, M i , j ∈ R k × k M_{i,j} \in R^{k \times k} Mi,j∈Rk×k,是要学习的参数。
建立self-matching information matrix : W ∈ R n × n W \in R^{n \times n} W∈Rn×n:

![]()
对 W W W每行取最大值,组成向量 m ∈ R n m \in R^n m∈Rn
⟹ a = S o f t m a x ( m ) ⟹ a ∈ R n \implies a=Softmax(m) \implies a \in R^n ⟹a=Softmax(m)⟹a∈Rn
Bi-LSTM
target: 利用Bi-LSTM的隐含层输出,作为输入句子的特征向量feature vector : f l ∈ R d ⟹ f l = h 1 f_l \in R^d \implies f_l=h_1 fl∈Rd⟹fl=h1,d是超参数, h i ∈ R d h_i \in R^d hi∈Rd。
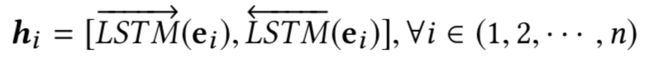
注:此处有个疑问,为什么只使用第一个时间步的输出呢?最后一个时间步的输出又如何呢?
Low-rank Bilinear Pooling
target: 融合上述两个模型得到的向量 f a ∈ R k , f l ∈ R d f_a \in R^k, f_l \in R^d fa∈Rk,fl∈Rd,得到最终的融合向量 f ∈ R c f \in R^c f∈Rc,并进行二分类,得到输出向量 p i ∈ R 2 p_i \in R^2 pi∈R2。c是超参数。
f = U T ⋅ f a ∘ V T ⋅ f l + b f=U^T \cdot f_a \circ V^T \cdot f_l + b f=UT⋅fa∘VT⋅fl+b
p i = S o f t m a x ( W f ⋅ f + b ) p_i=Softmax(W_f \cdot f + b) pi=Softmax(Wf⋅f+b)
其中, U ∈ R k × c , V ∈ R d × c , g ∈ R c , W f ∈ R 2 × c , b ∈ R 2 U \in R^{k \times c}, V \in R^{d \times c}, g \in R^{c}, W_f \in R_{2 \times c}, b \in R^2 U∈Rk×c,V∈Rd×c,g∈Rc,Wf∈R2×c,b∈R2,这些都是需要学习的参数。
注: ∘ \circ ∘ 表示 Hadamard Product,简单来说就是矩阵对应位置元素相乘。
训练目标:
![]()

待学习参数: θ = { M i , j , U , V , g , W f , b } \theta = \{ M_{i,j},U,V,g,W_f,b \} θ={Mi,j,U,V,g,Wf,b}
超参数: d , c , λ d, c, \lambda d,c,λ
