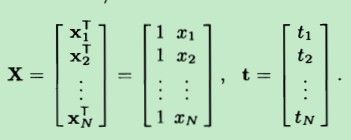
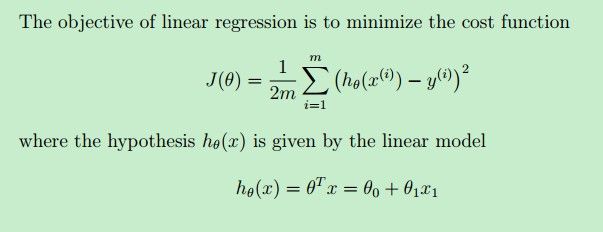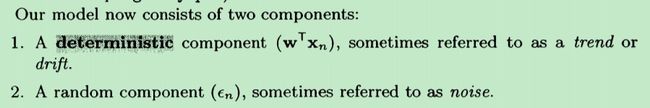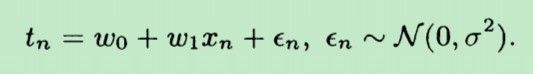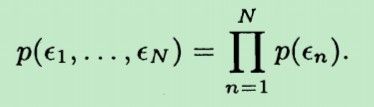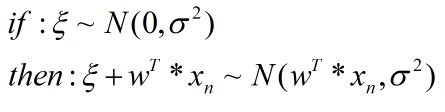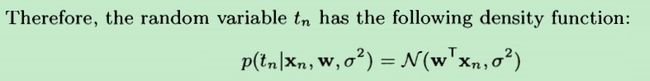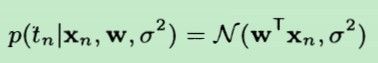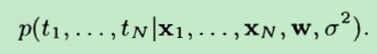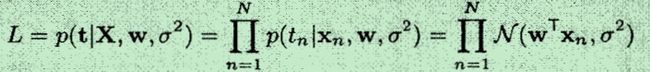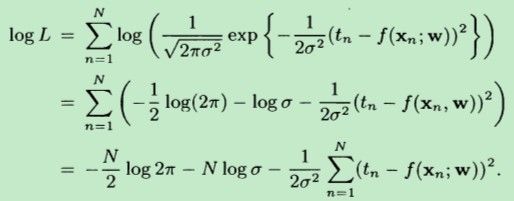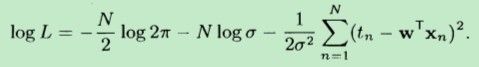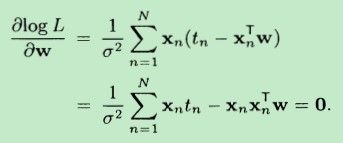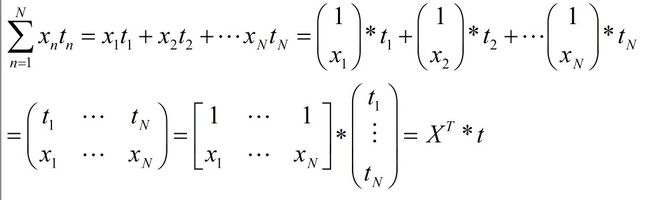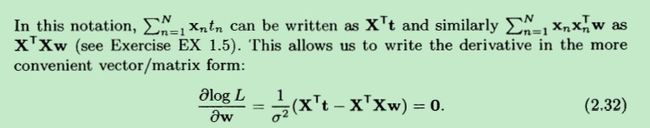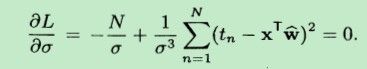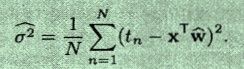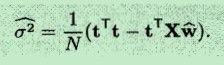最大似然函数及其求解
转自:http://www.cnblogs.com/hapjin/p/6623795.html
使用最大似然法来求解线性模型(1)
在Coursera机器学习课程中,第一篇练习就是如何使用最小均方差(Least Square)来求解线性模型中的参数。本文从概率论的角度---最大化似然函数,来求解模型参数,得到线性模型。本文内容来源于:《A First Course of Machine Learning》中的第一章和第二章。
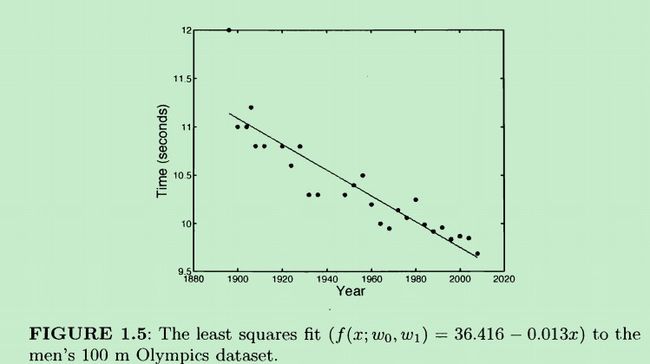
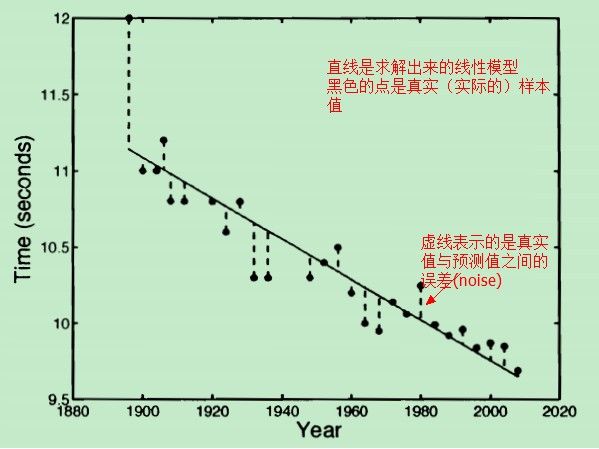
先来看一个线性模型的例子,奥林匹克百米赛跑的男子组历年数据如下:
所谓求得一个线性模型就是:给定一组数据(上图中的很多点),如何找到一条合适的直线,让这条直线能够更好地“匹配”这些点。
一种方式就是使用最小二乘法,通过最小化下面的代价函数J(θ)求得一条直线方程--即线性模型。
其中,hθ(x)是待求解的线性模型(本例中就是一条直线),y(i)是样本x(i)对应的实际值,hθ(x(i))是线性模型在样本x(i)上的预测值。我们的目标就是让实际值与预测值二者尽可能地接近--二者之间的“差”尽可能地小,这样我们的预测结果就越准确,我们的线性模型也越好(不考虑overfitting)
最小二乘法就是最小化J(θ)这个函数,解出θ,代入hθ(x),得到一条直线(hθ(x)就是直线方程)。而这条直线,就是我们的线性模型了。
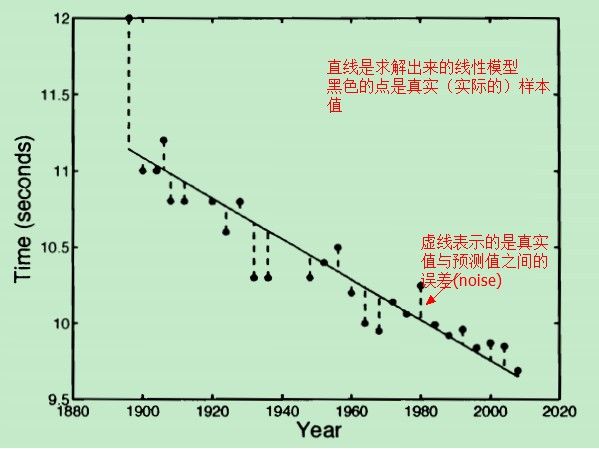
对于这种方式而言,我们的模型就是一条直线,在我们的模型中(直线)没有能够反映真实值与预测值之间的误差的因子。把模型稍微修改一下:
从原来的:(这里的w就相当于上面的θ,t 就是hθ(x),只是为了统一 一下《A First Course of Machine Learning》中用到的符号)
t=wT*x
改成:
t=wT*x+ξ
其中,ξ 用来表示“误差”---noise,x是训练样本数据,w是模型的参数。
这样,我们的新模型表达式:t=wT*x+ξ 就可以显示地表示 noise 了(不仅仅是一条直线表达式了)。那现在问题还是:怎样求得一个“最好的” w 和 ξ,得到“最好的”模型?
现在不是用上面的最小二乘法了求解w 和 ξ 了,而是用最大似然函数法---(见使用最大似然法来求解线性模型(2)-为什么是最大化似然函数?)
使用最大似然法来求解线性模型(2)-为什么是最大化似然函数?
根据 使用最大似然法来求解线性模型(1),待求解的线性模型如下式:
- tn=wT*xn+ξn
第xn年的百米赛跑的时间tn,与两个参数有关:一个是w,另一个则是该年对应的一个误差值(noise)
在求解w和 ξ 之前,先观察一下误差值的特点:
- 误差有正有负,是一个随机变量。
- 误差与年份无关,每一个年份对应的误差之间相互独立
因此,关于errors(noise)的假设如下:
更进一步,假设errors(noise)服从高斯分布,模型表示如下:显然这个模型由两个参数来决定:w 和 σ2,只要确定这两个参数,就确定了这个模型。
这N个误差的联合概率密度为:p(ξ1,ξ2,...,ξN),由于它们相互独立,故有:
现在,tn 表示成了一个常数(w0+w1*xn) 加上 一个服从高斯分布的随机变量ξn,故tn 也相当于一个服从正态分布的随机变量了。根据正态分布性质:
得出:
那tn为什么是个条件概率呢?
根据上面tn的表达式,在给定的w和ξn之后,我们就知道了tn。而ξn服从正态分布,由σ2来确定。故tn可表示成如上的条件概率形式。
现在不妨假设已经求得了w=[36.416,-0.0133]T和σ2=0.05,在xn=1980年时,上面的条件概率公式表示如下:
随机变量的均值由wT*xn计算得到,均值u=10.02,而方差是0.05
![]()
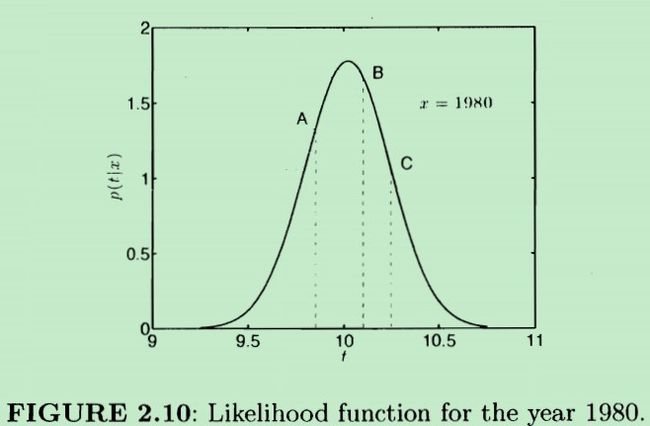
故它的概率密度函数如下:
在概率密度函数中有三个点A,B,C。其中B点对应的时间t约是tB=10.1,C点对应的时间t是tC=10.25
从图中可以看出:在A,B,C三个点中,B点对应的概率密度最大(y轴的值最高),根据正态分布的概率密度性质,说明随机变量取B点处的值的概率最大,也即:随机变量tn最可能的取值是10.1秒
但是,我们实际观察到的1980年奥林匹克竞赛男子100m赛跑的时间是:10.25秒,这是实际的样本值,也即上面概率密度函数中C点对应的值。
因此,问题就来了:
我们需要修改(重新求解)w和的σ2值(原来的值为:w=[36.416,-0.0133]T σ2=0.05),使得:根据w和σ2画出的概率密度函数在t=10.25处最高,也即在t=10.25处取值的概率最大。
换句话说:我们需要寻找合适的w和σ2,让模型的概率密度函数在 实际值10.25秒 时,对应的概率密度最大。
我们把实际的样本值t=10.25 称为样本点xn=1980 所对应的 似然值(likelihood of data point 1980)。
目标是:寻找合适的w和σ2 让概率密度函数在真实值10.25秒 时对应的概率密度最大。而这就是最大化似然函数的思想。
参考:《A First Course of Machine Learning》第二章
使用最大似然法来求解线性模型(3)-求解似然函数
根据 使用最大似然法来求解线性模型(2)-为什么是最大化似然函数? 中提到,某个随机变量tn的 条件概率 服从均值为wT*xn,方差为σ2的正态分布。
现在假设有N个样本点,它们的联合概率密度为:
由于在给定了w和σ2的条件下,tn之间是相互独立的,故联合概率密度可写成下式:
为什么 tn在给定了w和σ2的条件下是相互独立的呢?如果直接从图形上看,不是相互独立的,各个tn之间大致是一个单调的线性下降关系。也即:t1
这个单调下降的线性关系就是由 w 决定的(体现的)。
在给定了w的条件下,每年的奥林匹克男子100m时间的年份之间就没有必然的联系了,就好像16年奥运会男子100m的时间 与 06 年奥林匹克男子100m的时间 是没有关系,相互独立的。
但从整个历史趋势(1960-2020)来看,奥林匹克男子100m所花的时间是越来越少的。
这里需要注意的是:t是条件独立的,即在给定的w条件下,各个t之间是相互独立的。上面的 L 就是似然函数。
要想最大化L,相当于最大化logL,于是就有:
其中,f(x;w)=w*x,代入上式,得到:
让logL 对 w 求偏(将xn 、tn 和 δ 都视为常数),并令偏导数等于0,根据向量乘法:wT*xn = xnT * w。故得到:
需要注意的是:上式Xn是一个向量,XnT=[1,xn],表示的是年份,即哪一年的比赛数据,比如x10=1980。前面的1 是偏置项。
因为:wT*xn=w0*1+w1*xn. wT=(w0,w1)有两个参数,故需要一个bias unit(偏置项)
为什么w有两个参数(w0,w1)呢?因为我们是用直线来拟合数据。根据直线的一般表达式方程 y=k*x+b,需要两个参数,一个是斜率k,另一个是截距b
只要给定了斜率和截距,就能唯一确定一条直线了。而对于向量w,分量w0相当于截距,分量w1相当于斜率。
tn是一个标量,表示的是第n个样本点代表的年份,比如t10=10.25 表示第10个样本点所表示的奥林匹克男子100m所花的时间是10.25秒。
w是一个向量,即线性模型里面的模型参数。它们的具体形式如下(n 和 N 没有区别):
把求和累加化简,根据矩阵乘法:(注意下面x一个是向量,一个是单个实数x。它们之间的关系:XnT=[1,xn])
这样,我们就可以将偏导数表示成,更紧凑的矩阵乘法的形式,如下:
并最终求得w,结果用wΛ 来表示:
根据模型的概率密度函数:
还需要求解σ2。同样地,logL对σ求偏导数,并令偏导数等于0,得到下面公式:
最终解得为σ2:
将求得的wΛ 代入到上式(具体推导见参考文献),得到:
根据上面求解的w和δ2 的公式,现在只要给定若干个数据(训练样本X),就可以计算出w和δ2 ,从而求出了:
知道了概率密度表达式中所有的参数:w和δ2 ,当然也就求得了概率密度:
最终得出带有 ξn的能够估计 noise的“线性”模型。因为,此时我们的模型估计值tn是一个 随机变量了,随机变量的variance(各个点取值的偏差由δ2 决定)。
参考文献:《A First Course of Machine Learning》
原文:http://www.cnblogs.com/hapjin/p/6623795.html