Python数据结构与算法笔记(2)
problem-solving-with-algorithms-and-data-structure-using-python 中文版
3 基本数据结构
栈、队列、deques、列表是一类数据的容器,它们数据项之间的顺序由添加或删除的顺序决定。一旦一个数据项被添加,它相对于前后元素一直保持该位置不变。诸如此类的数据结构被称为线性数据结构。
线性数据结构有两端,有时候被称为左右、某些情况被称为前后,也可以称为顶部和底部。将两个线性数据结构区分开的方法是添加和移除项的方式,特别是添加和移除项的位置。
栈
后进先出LIFO,添加移除新项总发生在同一端。
栈的操作如下:
- Stack()创建一个空的新栈,不需要参数,并返回一个空栈
- push(item)将一个新项添加到栈的顶部,需要item作为参数,并不返回任何内容
- pop()从栈中删除顶部元素,不需要参数并返回item,栈被修改
- peek()从栈返回顶部项,但不会删除它,不需要参数,不修改栈
- isEmpty()测试栈是否为空。不需要参数,并返回布尔值
- size()返回栈中的item数量。不需要参数,并返回一个整数
简单括号匹配
区分括号是否匹配的能力是很多编程语言结构的重要部分。
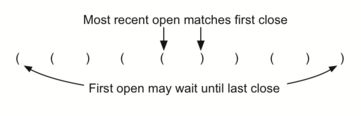
用栈来保存括号。从空栈开始,从左到右处理括号字符串。如果一个符号是开始符号,将其作为一个信号,对应的结束符号稍后会出现。另一方面,如果符号是结束符号,弹出栈,只要弹出栈的开始符号可以匹配每个结束符号,则括号保存匹配状态,如果任何时候栈上没有出现符合开始符号的结束符号,则字符串不匹配。最后,当所有符号都被处理后,栈应该是空的。
十进制转换成二进制
除2算法:
![]()
中缀表达式和后缀表达式
A+B*C中缀表达式,将运算符放在后面A B C * + 后缀表达式,*紧接着在B和C之后出现,表示*具有高的优先级,+优先级低。
中缀转后缀通用法:
当我们处理表达式时,操作符必须保存在某处,因为他们相应的右操作数还没有看到。此外,这些保存的操作符的顺序可能由于它们的优先级而需要翻转。这是在该示例中的加法和乘法的情况,由于加法运算符在乘法运算符之前,并且具有较低的优先级,因此需要在使用乘法运算符之后出现,由于这种顺序的翻转,考虑使用栈来保存运算符直到用到它们是有意义的
假设中缀表达式是一个由空格分隔的标记字符串。操作符是*,/,+,-,以及左右括号。操作数是单字符A,B,C等。以下步骤将后缀顺序生成一个字符串:
1. 创建一个名为opstack的空栈以保存运算符。给输出创建一个空列表。
2. 通过使用字符串方法拆分将输入的中缀字符串转换为标记列表
3. 从左到右扫描标记列表。
如果标记是操作数,将其附加到输出列表的末尾。
如果标记是左括号,将其压到opstack上
如果标记是右括号,则弹出opstack,直到删除相应的左括号,将每个运算符附加到输出列表的末尾
如果标记是运算符,*,/,+,-,将其压入opstack。但是,首先删除已经在opstack中具有更高或者相等优先级的任何运算符,并将它们加到输出列表中
4. 当输入表达式被完全处理时,检查opstack,仍然在栈上的任何运算符都可以删除并加到输出列表的末尾。后缀表达式求值:
在扫描后缀表达式时,必须等待操作数,另一种方法是每当在输入上看到运算符时,计算两个最近的操作数。
假设后缀表达式是一个由空格分隔的标记字符串。运算符为*,/,+,-,操作数假定为单个整数值,输出将是一个整数结果。
1. 创建一个名为operandStack的空栈。
2. 拆分字符串转换为标记列表。
3. 从左到右扫描标记列表。
如果标记是操作数,将其中字符串转换为整数,并将值压到operandStack
如果标记是运算符*,/,+,-,将需要两个操作数,弹出operandStack朗次。第一次弹出的是第二个操作数,第二个弹出的是第一个操作数。执行算术运算后,将结果压倒操作数栈中。
4. 当输入的表达式被完全处理后,结果就在栈上,弹出operandStack并返回值队列
队列是项的有序结合,其中添加新项的一端称为队尾,移除项的一段称为队首。当一个元素从队尾进入队列时,一直向队首移动,直到它称为下一个需要移除的元素为止。
最近添加的元素必须在队尾等待。集合中存活时间最长的元素在队首,这种排序称为FIFO,先进先出。
![]()
队列操作如下:
- Queue()创建一个空的新队列。不需要参数,并返回一个空队列
- enqueue(item)将新项添加到队尾。需要item作为参数,并不返回任何内容
- dequeue()从队首移除项,不需要参数并返回item,队列被修改
- isEmpyt()查看队列是否为空,不需要参数,并返回布尔值
- size()返回队列中的项数,不需要参数,返回一个整数
模拟:烫手山芋
![]()
模拟:打印机
1. 创建打印任务的队列,每个任务都有个时间戳。队列启动的时候为空。
2. 每秒(currentSecond):
是否创建新的打印任务?如果是,将currentSecond作为时间戳添加到队列
如果打印机不忙并且有任务在等待
从打印机队列中删除一个任务并将其分配给打印机
从currentSecond中减去时间戳,以计算该任务的等待时间
将该任务的等待时间附件到列表中稍后处理
根据打印任务的页数,确定需要多少时间
打印机需要一秒打印,所以得从该任务所需的等待时间减去一秒
如果任务已经完成,换句话说,所需的时间已经达到0,打印机空闲
3. 模拟完成后,从生成的等待时间列表中计算平均等待时间Deque 双端队列
双端队列是与队列类似的项的有序集合。有两个端部,首部和尾部,并且项在集合中保持不变,deque不同的地方是添加和删除项是非限制性的。可以在前面或后面添加新项。同样,可以在任一端移除现有项。在某种意义上,这种混合线性结构提供了单个数据结构中的栈和队列的所有能力。
![]()
Deque的操作:
- Deque()创建一个空的新deque,不需要参数,并返回空的deque
- addFront(item),将一个新的项添加到deque的首部,需要参数item,不返回任何内容
- addRear(item),将一个新项添加到deque的尾部。需要item参数并不返回任何内容
- removeFront(),从deque中删除首项。不需要参数并返回item。deque被修改
- removeRear(),从deque中删除尾项,不需要参数并返回item,deque被修改
- isEmpty(),测试deque是否为空,不需要参数,并返回布尔值
- size()返回deque中的项数。不需要参数,并返回一个整数
回文检查:
![]()
列表
无序列表的结构是项的集合,其中每个项保持相对于其他项的相对位置。无序列表可能的操作:
- List()创建一个新的空列表,不需要参数,并返回一个空列表
- add(item)向列表中添加一个新项,需要item作为参数,不返回任何内容,假定item不在该列表中
- remove(item),从列表中移除该项,需要item作为参数并修改列表,假设项存在于列表中
- search(item)搜索列表中的项目,需要item作为参数,并返回一个布尔值
- isEmpty()检查列表是否为空,不需要参数,并返回布尔值
- size()返回列表中的项数,不需要参数,返回一个整数
- append(item)将一个新项添加到列表的末尾,使其成为集合中的最后一项。需要item作为参数,并不返回任何内容,假定该项不在列表中
- index(item)返回项在列表中的位置,需要item作为参数并返回索引,假定项在改列表中
- insert(pos,item)在位置pos处向列表中添加一个新项,需要item作为参数并不返回任何内容,假设该项不在列表中,并且有足够的现有项使其有pos位置
- pop()删除并返回列表中的最后一个项,假设该列表至少有一个项
- pop(pos)删除并返回位置pos处的值,需要pos作为参数并返回项,假定该项在列表中
有序列表是项的结合,其中每个项保存基于项的一些潜在的特性的相对位置,排序通常是升序或降序,并且我们假设列表具有已经定义的有意义的比较运算,需要有序列表操作与无序列表操作相同:
- OrderedList()创建一个新的空列表,不需要参数,返回一个空列表
- add(item)向列表中添加一个新项,需要item作为参数,并不返回任何内容,假定item不在列表中
- remove(item)从列表中删除该项,需要item作为参数并修改列表,假设项存在于列表中
- search(item)搜索列表中的项目,需要item作为参数,并返回一个布尔值
- isEmpty()检查列表是否为空,不需要参数,并返回布尔值
- size()返回列表中的项数,不需要参数,返回一个整数
- index(item)返回项在列表中的位置,需要item作为参数并返回索引,假定该项在列表中
- pop()删除并返回列表中的最后一个项,假定该列表至少有一个项
- pop(pos)删除并返回位置pos出的项,需要pos作为参数,返回项,假定该项在列表中