CS131学习笔记（lecture7）

讲义地址：http://vision.stanford.edu/teaching/cs131_fall1718/files/07_DoG_SIFT.pdf
上节说到，Harris检测器对于尺度变换下的关键点检测效果不理想，所以本节将关注一些在尺度变换下依然可以有效检测的方法。

尺度不变检测

从直觉上，我们在进行不同尺度下的特征检测时，需要选取范围不同的窗函数（以下以圆圈为例），即：对比例尺较小的图像选取范围较小的窗函数；对比例尺较大的图像选取范围更大的窗函数。

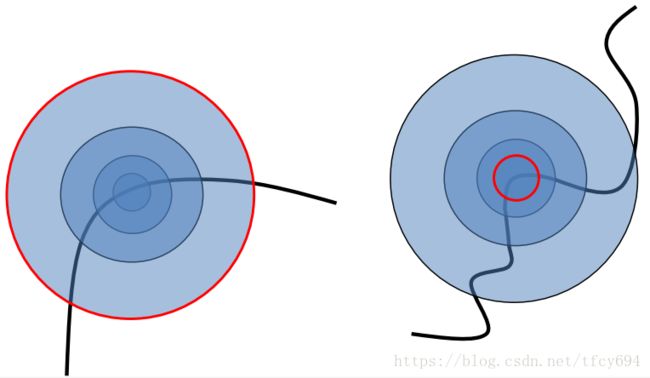
那么具体如何选定这些窗函数的范围呢？我们可以把每一个像素点周围的点的像素值作为范围（如半径）的函数，选取一个特征比较明显的点（如峰值），选取所对应的自变量就能在若干幅图中【独立】地确定窗函数的范围。当然了，这种“独立”也对图像的普适性作出了一定的牺牲。图像的像素函数需要满足：有且仅有一个峰值明显的点。这样才不会误导算法作出错误的选择。


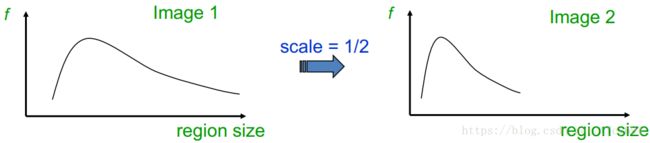
以上思路在数学上表示为一个kernel函数和图像函数的卷积。

关于这个kernel的形式，一种是一个高斯拉普拉斯算子（Laplace of Gaussian，LoG）¹：$$L={\sigma }^2(G_{xx}(x,y,\sigma )+G_{yy}(x,y,\sigma )))$$

其数学原理是：对于图像$f$，首先进行高斯平滑处理滤去噪点：$$G(x,y,\sigma )\ast f(x,y)$$然后对上式求得微分，进行边缘检测：$$\frac{d}{dx}(G\ast f)=\frac{dG}{dx}\ast f$$其中，二阶形式的微分$\frac{dG}{dx}$即是拉普拉斯算子。
该算法相当有效，但是也要求了更高的计算复杂度。所以可以用一个高斯差分算子(Difference of Gaussians, DoG)²来近似LoG滤波器：$$DoG=G(x,y,k\sigma )-G(x,y,\sigma )$$

本节中，$G(x,y,\sigma )$表示均值为1的高斯函数。
基于DoG算子，可以采用SIFT算法进行特征匹配。

高斯金字塔（octave）

DoG中常对一幅图像分别以$\sigma$, $2\sigma$, …, $k\sigma$做出$k$个卷积结果，构成金字塔，然后对金字塔的不同层进行差分，即可获得差分金字塔。从而得到稳定的特征。差分金字塔的每一层都可以看做一个带通滤波器的响应（特定分辨率的图像减去一个模糊的低频图像），所以各层金字塔分别表征了图像在不同频率下的响应。可以在全图范围内根据DoG选取相应的兴趣点和窗函数范围。

尺度不变特征变换（Scale Invirant Feature Transform, SIFT)

检测问题主要分为寻找关键点和匹配问题。前面我们都是使用Harris角检测器寻找角作为关键点，上面介绍了基于DoG的尺度不变检测算法，得到了一些keypoint和相应的独立的scaling范围。SIFT中的关键点匹配方法则是基于梯度方向直方图的。
算法：

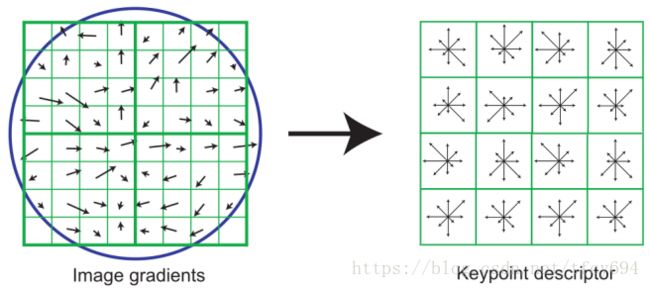
对于每一个keypoint，计算scaling范围中各点处的梯度，并减去待匹配keypoint的rotation角度，从而实现旋转不变。
将相应的scaling范围划分成4*4的方格，对每个方格中的像素点统计梯度并近似到8个方向，reshape成为128维的向量。
对于所有keypoints得到的向量，用欧氏距离进行匹配即可。

一些讨论：
由于以上过程是基于梯度的，所以整体的光照增强和减弱不影响匹配效果。
对比度会影响梯度的变化，此情况下要进行归一化处理。

另一种描述子：梯度方向直方图（Histogram of Oriented Gradients，HoG）

前面介绍了一些尺度可变和尺度不变的匹配算法，现在介绍一种作为SIFT的variant的、广泛用于人形识别的图像描述算法——HoG。

把全图划分成一系列（矩形或圆形）的空间区域（称为cell）
对于每个cell，统计所包含的像素点的近似梯度并建立直方图。
在包含若干个cells的更大范围（称为block）内进行normalize。

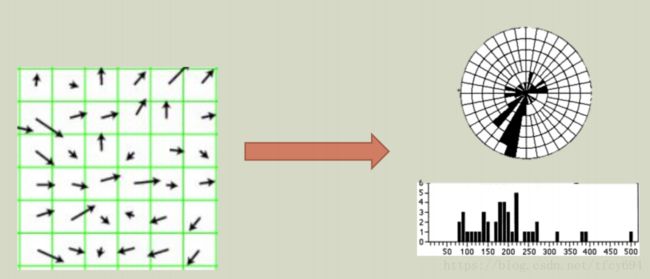
通过对原图进行以上处理，则可以根据不同的需要提取相应的不同的信息。如下：

HoG的一些缺点：
1.检测范围广。
2.慢。
3.当背景光照有差异时，识别效率不太高。
##全景拼接
全景拼接在lab中有详细的过程，此处仅对过程作简要介绍：

1.检测keypoint
2.（利用RANSAC）建立并匹配descriptor
3.根据匹配结果建立仿射变换、

---

1. http://ieeexplore.ieee.org/document/937561/ (没错，我们总算进入21世纪了) ↩︎

2. https://dl.acm.org/citation.cfm?id=996342 ↩︎