使用pytorch快速搭建神经网络实现二分类任务(包含示例)
Introduce
上一篇学习笔记介绍了不使用pytorch包装好的神经网络框架实现logistic回归模型,并且根据autograd实现了神经网络参数更新。
本文介绍利用pytorch快速搭建神经网络。即利用torch.nn以及torch.optim库来快捷搭建一个简单的神经网络来实现二分类功能。
- 利用pytorch已经包装好的库(torch.nn)来快速搭建神经网络结构。
- 利用已经包装好的包含各种优化算法的库(torch.optim)来优化神经网络中的参数,如权值参数w和阈值参数b。
以下均为初学者笔记。
Build a neural network structure
假设我们要搭建一个带有两个隐层的神经网络来实现节点的二分类,输入层包括2个节点(输入节点特征),两个隐层均包含5个节点(特征映射),输出层包括2个节点(分别输出属于对应节点标签的概率)。如下图所示:
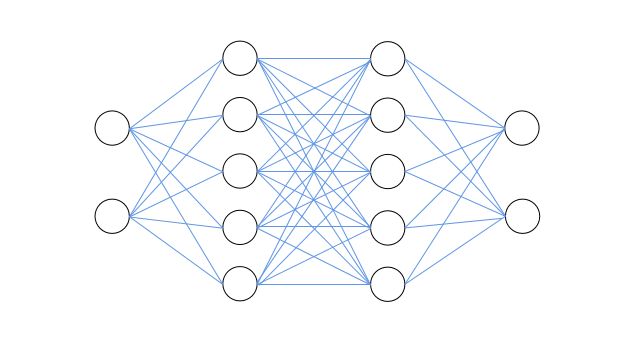
上图从左右到右为输入层、隐藏层、隐藏层、输出层,各层之间采用全连接结构。神经网络两隐藏层的激活函数均采用sigmoid函数,输出层最后采用softmax函数归一化概率。
网络搭建过程中使用的torch.nn相关模块介绍如下:
- torch.nn.Sequential:是一个时序容器,我们可以通过调用其构造器,将神经网络模块按照输入层到输出层的顺序传入,以此构造完整的神经网络结构,具体用法参考如下神经网络搭建代码。
- torch.nn.Linear:设置网络中的全连接层,用来实现网络中节点输入的线性求和,即实现如下线性变换函数:
\[y = xA^T + b \]
'''
搭建神经网络,
输入层包括2个节点,两个隐层均包含5个节点,输出层包括1个节点。'''
net = nn.Sequential(
nn.Linear(2,5), # 输入层与第一隐层结点数设置,全连接结构
torch.nn.Sigmoid(), # 第一隐层激活函数采用sigmoid
nn.Linear(5,5), # 第一隐层与第二隐层结点数设置,全连接结构
torch.nn.Sigmoid(), # 第一隐层激活函数采用sigmoid
nn.Linear(5,2), # 第二隐层与输出层层结点数设置,全连接结构
nn.Softmax(dim=1) # 由于有两个概率输出,因此对其使用Softmax进行概率归一化,dim=1代表行归一化
)
print(net)
'''
Sequential(
(0): Linear(in_features=2, out_features=5, bias=True)
(1): Sigmoid()
(2): Linear(in_features=5, out_features=5, bias=True)
(3): Sigmoid()
(4): Linear(in_features=5, out_features=2, bias=True)
(5): Softmax(dim=1)
)'''
Configure Loss Function and Optimizer
note: torch.optim库中封装了许多常用的优化方法,这边使用了最常用的随机梯度下降来优化网络参数。例子中使用了交叉熵损失作为代价函数,其实torch.nn中也封装了许多代价函数,具体可以查看官方文档。对于pytorch中各种损失函数的学习以及优化方法的学习将在后期进行补充。
配置损失函数和优化器的代码如下所示:
# 配置损失函数和优化器
optimizer = torch.optim.SGD(net.parameters(),lr=0.01) # 优化器使用随机梯度下降,传入网络参数和学习率
loss_func = torch.nn.CrossEntropyLoss() # 损失函数使用交叉熵损失函数
Model Training
神经网络训练过程大致如下:首先输入数据,接着神经网络进行前向传播,计算输出层的输出,进而计算预先定义好的损失(如本例中的交叉熵损失),接着进行误差反向传播,利用事先设置的优化方法(如本例中的随机梯度下降SGD)来更新网络中的参数,如权值参数w和阈值参数b。接着反复进行上述迭代,达到最大迭代次数(num_epoch)或者损失值满足某条件之后训练停止,从而我们可以得到一个由大量数据训练完成的神经网络模型。模型训练的代码如下所示:
# 模型训练
num_epoch = 10000 # 最大迭代更新次数
for epoch in range(num_epoch):
y_p = net(x_t) # 喂数据并前向传播
loss = loss_func(y_p,y_t.long()) # 计算损失
'''
PyTorch默认会对梯度进行累加,因此为了不使得之前计算的梯度影响到当前计算,需要手动清除梯度。
pyTorch这样子设置也有许多好处,但是由于个人能力,还没完全弄懂。
'''
optimizer.zero_grad() # 清除梯度
loss.backward() # 计算梯度,误差回传
optimizer.step() # 根据计算的梯度,更新网络中的参数
if epoch % 1000 == 0:
print('epoch: {}, loss: {}'.format(epoch, loss.data.item()))
'''
每1000次输出损失如下:
epoch: 0, loss: 0.7303197979927063
epoch: 1000, loss: 0.669952392578125
epoch: 2000, loss: 0.6142827868461609
epoch: 3000, loss: 0.5110923051834106
epoch: 4000, loss: 0.4233965575695038
epoch: 5000, loss: 0.37978556752204895
epoch: 6000, loss: 0.3588798940181732
epoch: 7000, loss: 0.3476340174674988
......
'''
print("所有样本的预测标签: \n",torch.max(y_p,dim = 1)[1])
'''
note:可以发现前100个标签预测为0,后100个样本标签预测为1。因此所训练模型可以正确预测训练集标签。
所有样本的预测标签:
tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1])
'''
网络的保存和提取
'''两种保存方式
第一种: 保存网络的所有参数(包括网络结构)
torch.save(net,'net.pkl')
对应加载方式: net1 = torch.load('net.pkl')
第二种: 仅保存网络中需要训练的参数 ,即net.state_dict(),如权值参数w和阈值参数b。(不包括网络结构)
torch.save(net.state_dict(),'net_parameter.pkl')
对应加载方式:
加载时需要提供两个信息:
第一: 网络结构信息,需要先重新搭建和保存的网络同样的网络结构。
第二: 保存的网络中的参数的信息,权值和阈值参数。
具体加载方式如下:
net = nn.Sequential(
nn.Linear(2,5),
torch.nn.Sigmoid(),
nn.Linear(5,5),
torch.nn.Sigmoid(),
nn.Linear(5,2),
nn.Softmax(dim=1)
)
net2.load_state_dict(torch.load('net_parameter.pkl')
'''
本文参考-1
本文参考-2
附完整代码
import torch
import torch.nn as nn
'''
使用正态分布随机生成两类数据
第一类有100个点,使用均值为2,标准差为1的正态分布随机生成,标签为0。
第二类有100个点,使用均值为-2,标准差为1的正态分布随机生成,标签为1。
torch.normal(tensor1,tensor2)
输入两个张量,tensor1为正态分布的均值,tensor2为正态分布的标准差。
torch.normal以此抽取tensor1和tensor2中对应位置的元素值构造对应的正态分布以随机生成数据,返回数据张量。
'''
x1_t = torch.normal(2*torch.ones(100,2),1)
y1_t = torch.zeros(100)
x2_t = torch.normal(-2*torch.ones(100,2),1)
y2_t = torch.ones(100)
x_t = torch.cat((x1_t,x2_t),0)
y_t = torch.cat((y1_t,y2_t),0)
'''
搭建神经网络,
输入层包括2个节点,两个隐层均包含5个节点,输出层包括1个节点。
'''
net = nn.Sequential(
nn.Linear(2,5), # 输入层与第一隐层结点数设置,全连接结构
torch.nn.Sigmoid(), # 第一隐层激活函数采用sigmoid
nn.Linear(5,5), # 第一隐层与第二隐层结点数设置,全连接结构
torch.nn.Sigmoid(), # 第一隐层激活函数采用sigmoid
nn.Linear(5,2), # 第二隐层与输出层层结点数设置,全连接结构
nn.Softmax(dim=1) # 由于有两个概率输出,因此对其使用Softmax进行概率归一化
)
print(net)
'''
Sequential(
(0): Linear(in_features=2, out_features=5, bias=True)
(1): Sigmoid()
(2): Linear(in_features=5, out_features=5, bias=True)
(3): Sigmoid()
(4): Linear(in_features=5, out_features=2, bias=True)
(5): Softmax(dim=1)
)'''
# 配置损失函数和优化器
optimizer = torch.optim.SGD(net.parameters(),lr=0.01) # 优化器使用随机梯度下降,传入网络参数和学习率
loss_func = torch.nn.CrossEntropyLoss() # 损失函数使用交叉熵损失函数
# 模型训练
num_epoch = 10000 # 最大迭代更新次数
for epoch in range(num_epoch):
y_p = net(x_t) # 喂数据并前向传播
loss = loss_func(y_p,y_t.long()) # 计算损失
'''
PyTorch默认会对梯度进行累加,因此为了不使得之前计算的梯度影响到当前计算,需要手动清除梯度。
pyTorch这样子设置也有许多好处,但是由于个人能力,还没完全弄懂。
'''
optimizer.zero_grad() # 清除梯度
loss.backward() # 计算梯度,误差回传
optimizer.step() # 根据计算的梯度,更新网络中的参数
if epoch % 1000 == 0:
print('epoch: {}, loss: {}'.format(epoch, loss.data.item()))
'''
torch.max(y_p,dim = 1)[0]是每行最大的值
torch.max(y_p,dim = 1)[0]是每行最大的值的下标,可认为标签
'''
print("所有样本的预测标签: \n",torch.max(y_p,dim = 1)[1])