Julia 求解ODE方程
新学习Julia,每天晚上写一小段学习笔记。都比较肤浅,主要是为了给自己看的,如果有人感兴趣,也可以交流,互相学习。由于我是从零学起,从Fortran直接转到julia,差别还是很大的,所以我也会从零开始介绍。
在开始前先介绍下julia和包的安装,julia在官网可以直接下载,或者在juliabox.com上直接在线使用,但是由于julia服务器有限,一道网上经常上不去,所以还是建议在本地使用juliapro或者jupyter notebooks。
Jupyter notebooks用起来非常方便好用,具体的可以随便搜一下就有大把介绍,在notebook里可以编译执行几乎所有语言,在julia命令行里安装的话也很方便,下面介绍下包的安装。
julia的包都依托在 github上,安装的话,在julia命令行(或者jupyter notebook)下执行,
using Pkg #1.0版本需要执行这个,之前的版本比如0.6不需要
比如安装IJulia 也就是jupyter notebook一套东西,先更新下已有包,避免依赖问题
Pkg.update() Pkg.add("IJulia")然后根据提示,可能还需要build一下
Pkg.build("IJulia")然后使用包
using IJulia
notebook()言归正传,DifferentialEquations.jl
Pkg.add("DifferentialEquations")这个包需要很多包的依赖,所以安装会比较久一点点。其它包也是类似的,我会边学变记录一下自己所用的包。 目前是2018.9.13,julia 的1.0版本还不能使用该包,可能还没有随着版本进行更新。在0.64版本用起来没有问题的。
该包http://docs.juliadiffeq.org/latest/index.html 包括各种ODEs SODEs DAEs DDEs 还有一些PDEs可以求解。 该包计算效率甚至比c和fortran都高。官网有详细的介绍和说明,我也是从官方文档学起的
下面举一个简单的标量方程例子
其中 f(u,p,t)=αu f ( u , p , t ) = α u ,求解区间为 [0,1] [ 0 , 1 ] 。先看一下求解代码:
引用块内容
using DifferentialEquations
f(u,p,t) = 1.01u
u0=1/2
tspan = (0.0,1.0)
prob = ODEProblem(f,u0,tspan)
sol = solve(prob,Tsit5(),reltol=1e-8,abstol=1e-8)
# 下面是画图
using Plots
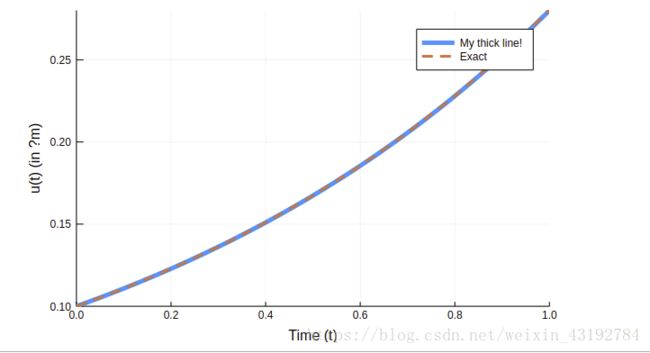
plot(sol,linewidth=5,title="Solution to the linear ODE with a thick line",
xaxis="Time (t)",yaxis="u(t) (in μm)",label="My Thick Line!") # legend=false
plot!(sol.t, t->0.5*exp(1.01t),lw=3,ls=:dash,label="True Solution!")
发现Plots包 居然不支持中文和希腊字母,不应该是这样,回头在仔细研究PLots包,看问题在哪。
对求解的每一块进行简单分析,
首先需要定义一个函数,也就是ODE右端项,Julia里面定义函数的方式有两种(三种?) 复杂的函数可以用function块
function f(u,t,p)
return 1.01u #其中1.01u是1.01×u的缩写,很直观是不是
end
简单的函数直接可以通过
f(u,t,p)=1.01u这种简单方式定义。
或者写成
f(u,t,p)= u -> 1.01u也是可以的。
然后定义求解的初始值和求解区域,这都是很必要的。
然后给出需要求解问题的类。
第二步,调用求解函数
其中可以选用多种ODE求解方法,可以选用的求解方法很多,
AutoTsit5(Rosenbrock23()) 可以求解刚性和非刚性问题,对于未知系统来说是极好的选择。
BS3() 高速求解非刚性问题。
Tsit5() 求解非刚性问题。
Vern7() 高阶非刚性方法。
Rodas4() 刚性方法。
radau() 高精度刚性方法(需要安装包ODEInterfaceDiffEq.jl)
solve里面通知控制误差来选择步长。reltol是相对误差,abstol是绝对误差,不需要都给出,省略一个也没关系,同时还可以控制输出步长,saveat=0.1 这样控制0.1存一次。
然后就是画图的问题啦。
我们还可以对解进行一系列分析,如
sol[5] #给出第五个输出值
sol.t[8] #第八个时间步
sol(0.45) #甚至可以插值出0.45的值。先这样,明天学一下ODEs方程组求解过程。