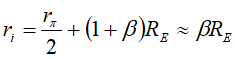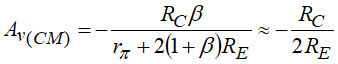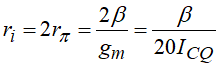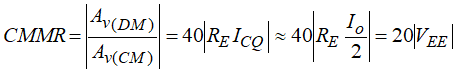电子电路:差分放大器分析
1. 差分放大器与共模抑制比
1.1差分放大器
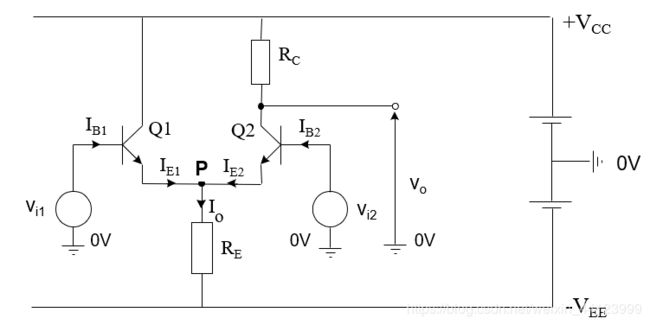
差分放大器有两个输入端和一个输出端,它可以获取两个输入电压之间的差值,并将这个差值放大后送到输出端,差分放大器的模型如下:
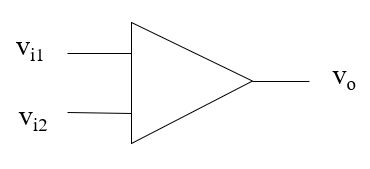
输入电压 v i 1 , v i 2 v_{i1}, v_{i2} vi1,vi2与输出 v o v_o vo的关系为:
v o = A d ( v i 1 − v i 2 ) v_o=A_d(v_{i1}-v_{i2}) vo=Ad(vi1−vi2)
其中 A d A_d Ad是差分放大器的放大倍数
对于一个理想的差分放大器,如果一个信号同时加给放大器的两个输入端,则 v i 1 = v i 2 → v o = 0 v_{i1}=v_{i2}\rightarrow v_o=0 vi1=vi2→vo=0
这种同时出现在两个输入端的信号叫做共模信号(common mode signal)
可惜的是,实际中的共模信号仍然会产生一个很小的输出电压,如何区分一个差分放大器的好坏,就看它能不能在接收到不同信号时提供高增益,而在收到共模信号时提供低增益,不同信号对应增益的比值就是共模抑制比(CMRR),因此,一个差分放大器的品质可以用它的共模抑制比来表示
有一点要注意的是,共模信号 v i c v_{ic} vic在两个输入端的差值并不是 v i 1 − v i 2 v_{i1}-v_{i2} vi1−vi2,而是 v i 1 + v i 2 2 \frac{v_{i1}+v_{i2}}{2} 2vi1+vi2,既两个输入端电压的平均值
了解了差分放大器的功能后,我们来看一看差分放大器可以用来干什么。
在实际应用中,我们常常需要放大一些很微弱的交流电信号,但是很多不必要的干扰信号(噪声),可能也会被放大器捕获并彻底掩盖我们真正想要得到的信号。假如我们使用差分放大器来处理信号,由于被捕获的干扰信号在两个输入端一般是一致的,所以干扰信号会被认定为是共模信号,而我们需要的信号则通常是交流差模信号。因此,只有我们想要的信号会被放大,可以很好地提升信噪比。
举个例子,我们输入一个交流信号时, v i 1 = 50 μ V , v i 2 = − v i 1 = − 50 μ V v_{i1}=50\mu V, v_{i2}=-v_{i1}=-50\mu V vi1=50μV,vi2=−vi1=−50μV
此时我们可以得到差模输出电压为 v i 1 − v i 2 = 100 μ V v_{i1}-v_{i2}=100\mu V vi1−vi2=100μV
而此时的共模输出电压为 v i 1 + v i 2 2 = 0 μ V \frac{v_{i1}+v_{i2}}{2}=0\mu V 2vi1+vi2=0μV
假如此时出现噪声,导致输入两端的电压都增加了 1000 μ V 1000\mu V 1000μV,此时的差模输出电压不会改变,仍为 v i 1 − v i 2 = 100 μ V v_{i1}-v_{i2}=100\mu V vi1−vi2=100μV,这就避免了噪声干扰
下图可以帮助我们更直观的看到差分放大器的效果:

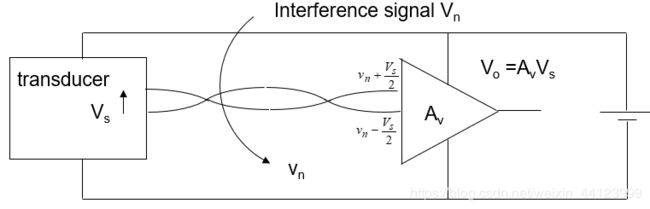
上面第一幅图是普通的放大器,可以看到干扰信号 V n V_n Vn和我们需要的信号 V s V_s Vs一起被放大了,使得输出信号 V o V_o Vo充满噪声
第二幅图是差分放大器,可以看到输入端两个信号的差值正好是我们需要的信号 V s V_s Vs,所以输出的结果不含干扰信号 V n V_n Vn,是信噪比非常低的信号
1.2 共模抑制比
一个差分放大器的共模抑制比代表了这个放大器的品质
它能告诉我们这个放大器可以多好地避免共模信号(CM)影响到我们想要的差分信号(DM)
我们定义共模抑制比的计算方式为:
C M R R = ρ = ∣ A d A c ∣ CMRR=\rho=|\frac{A_d}{A_c}| CMRR=ρ=∣AcAd∣
其中 A d A_d Ad是差分信号对应的增益, A c A_c Ac是共模信号对应的增益
共模抑制比越大,差分放大器的品质就越好
2. 长尾式差分放大电路以及它的交流/直流分析
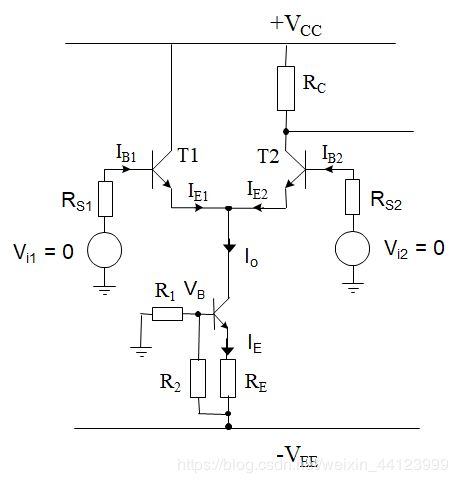
2.1 DC分析
对电路做直流分析时,我们要假设两个AC输入信号 v i 1 , v i 2 v_{i1}, v_{i2} vi1,vi2为0,此时两个晶体管基极电压都为0,而正向偏置的基极-射电极二极管压降约为0.6V,因此,通过电阻 R E R_E RE的电流为:
I o = V E E − 0.6 2 R E I_o=\frac{V_{EE}-0.6}{2R_E} Io=2REVEE−0.6
在长尾式差分放大电路中,两个晶体管 Q 1 , Q 2 Q_1,Q_2 Q1,Q2是完全一样的,因此,流过的电流也相同,根据KCL,可以得到晶体管的电流为:
I C Q = V E E − 0.6 2 R E I_{CQ}=\frac{V_{EE}-0.6}{2R_E} ICQ=2REVEE−0.6
接着,我们需要用KVL对电路进行分析:
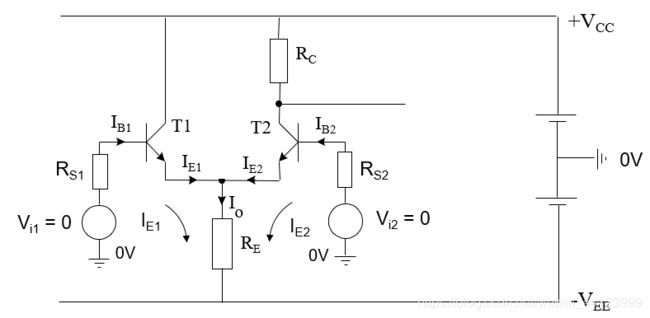
可以看到,这里增加了两个电阻 R S 1 , R S 2 R_{S1}, R_{S2} RS1,RS2,虽然图上不太直观,但 V i 1 , V i 2 V_{i1}, V_{i2} Vi1,Vi2下面是GND,实际上与最右边电源处的GND是相连的,因此构成如图所示的两个回路:
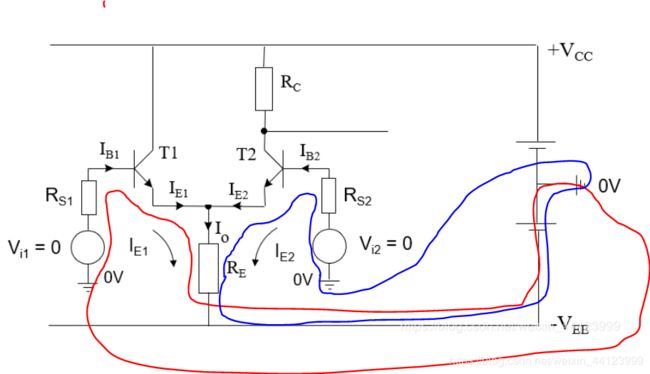
对这两个回路应用KVL,得到如下关系式:
![]()
![]()
对于这个电路,放大器两边的电阻,电流,电压应该是对称的,即:
![]()
这样之前用KVL得到的两个方程就可以化简成一个:
![]()
接着,根据 I E = I C + I B = ( β + 1 ) I B I_E=I_C+I_B=(\beta+1)I_B IE=IC+IB=(β+1)IB,我们可以用 I E I_E IE代替式子中的 I B I_B IB,得到:
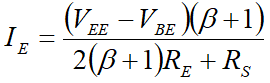
在实际中,几乎可以确定的是 2 ( β + 1 ) R E > > R S 2(\beta+1)R_E>>R_S 2(β+1)RE>>RS,因此可以将 R S R_S RS消去:
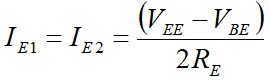
这个方程确定了我们在最早得出的结果,但它也说明了关系式的成立需要哪些条件
注意,流过两个晶体管的电流与电阻 R C R_C RC没有关系, R C R_C RC只是确保三极管不会在电压摇摆时饱和
2.2 AC分析
2.2.1 共模输入电阻
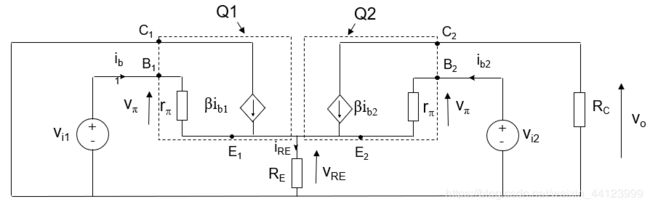
对于共模信号,输入电压 v i 1 , v i 2 v_{i1}, v_{i2} vi1,vi2被认为来自同一个电源 v i v_i vi,此时的电路图如下:
v i v_i vi产生的总电流为 i b 1 + i b 2 = i i i_{b1}+i_{b2}=i_i ib1+ib2=ii
对 v i , R E , v π v_i, R_E, v_\pi vi,RE,vπ围绕的环路作KVL,可以得到:
v i = v π + v R E v_i=v_\pi+v_{RE} vi=vπ+vRE
v i = i i r π 2 + ( β i b 1 + β i b 2 + i b 1 + i b 2 ) R E v_i=i_i\frac{r_\pi}{2}+(\beta i_{b1}+\beta i_{b2}+i_{b1}+i_{b2})R_E vi=ii2rπ+(βib1+βib2+ib1+ib2)RE
v i = i i r π 2 + i i ( 1 + β ) R E v_i=i_i\frac{r_\pi}{2}+i_i(1+\beta)R_E vi=ii2rπ+ii(1+β)RE
r i ( c o m m o n ) = v i i i = r π 2 + ( 1 + β ) R E r_i(common)=\frac{v_i}{i_i}=\frac{r_\pi}{2}+(1+\beta)R_E ri(common)=iivi=2rπ+(1+β)RE
2.2.2 共模电压增益
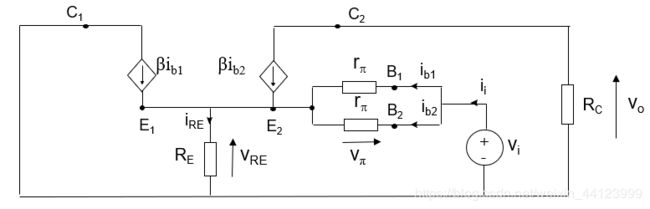
假设流经 R C R_C RC的电流为 i C 2 i_{C2} iC2,如图:

可以得到:
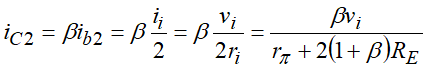
注意,只有穿过三极管Q2的电流会流经 R C R_C RC
电阻 R C R_C RC两端的电压就是输出电压,为:
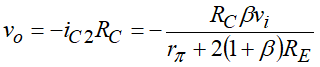
用输出电压 v o v_o vo除以输入电压 v i v_i vi,可以得到共模增益 A v ( C M ) A_v(CM) Av(CM)为:
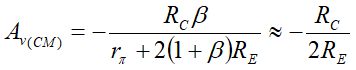
从上式中我们可以看出, R E R_E RE越大,共模时的电压增益就越小
2.2.3差分输入电阻
对于差模信号, v i 1 = − v i 2 v_{i1}=-v_{i2} vi1=−vi2,且 i b 1 = − i b 2 i_{b1}=-i_{b2} ib1=−ib2,等效电路如下:
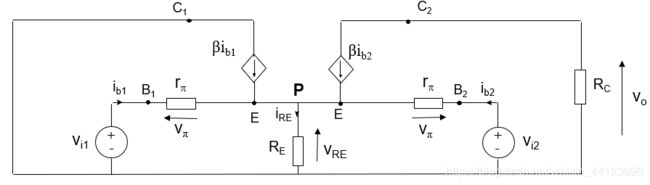
此时 v i 1 , v i 2 v_{i1}, v_{i2} vi1,vi2产生的增益后的电流会互相抵消,通过 R E R_E RE的电流不变???,点P的电势也不会改变
可以观察到,输入电阻为 2 r π = 2 β g m = β 20 I C Q 2r_{\pi}=\frac{2\beta}{g_m}=\frac{\beta}{20I_{CQ}} 2rπ=gm2β=20ICQβ
因此,较低的 I C Q I_{CQ} ICQ可以增大输入电阻
2.2.4 差分电压增益
因为施加在两个三极管基极的电压大小相等,方向相反,P点的电势保持它在直流时的值???
输出电压为:
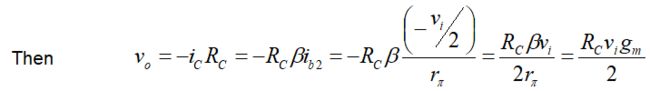 ???
???
则电压增益为 v o / v i v_o/v_i vo/vi等于
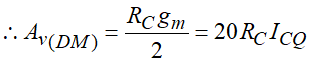
注意这里只能算半个共发射极放大电路(CE),因为输入信号被平分给了两个三极管,只有一半给了CE,也只有施加给Q2的信号才会对流经 R C R_C RC的输出电流有影响
2.2.5 小结
2.2.5.1 共模
输入电阻
电压增益
2.2.5.2 差模
输入电阻
电压增益
2.2.5.3 共模抑制比
2.2.5.4 技术总结
- 为了减小共模电压增益,我们需要增大 R E R_E RE
- 为了增大差模电压增益,我们需要增大 R C I C Q R_CI_{CQ} RCICQ(但不能超过 V C C V_{CC} VCC)
- 为了增大共模输入阻抗,我们需要增大 R E , β R_E, \beta RE,β
- 为了增大差模输入阻抗,我们需要减小 I C Q I_{CQ} ICQ,增大 β \beta β
3. 设计差分放大器
在2.2.5.4中,我们了解了差分放大器的一些设计要点,并且知道一个优秀的设计应该尽量增大 R E , R C I C Q , β R_E, R_CI_{CQ}, \beta RE,RCICQ,β
我们有以下几种方式增大 β \beta β
- 超增益晶体管
- 用一对晶体管连接在输入上形成达林顿对
- 用场效应晶体管取代双极晶体管,这会在电流镜中提到
在增大 R E R_E RE上,最好的方法是将 R E R_E RE替换为一个不变的电流源(一个完美的电流源理论上拥有无限大的电阻),而三极管的输出特性与一个不变的电流源非常接近,因此我们可以用一个三极管来代替 R E R_E RE,得到的电路图如下: