计算机基础与组成原理学习

二进制

背后的故事

盖房子

在很久很久以前，有一个原始部落，由一群头脑简单却四肢发达的人群集结而成，他们通过个人力量划分身份等级，最终决出一位部落首领，八位部落勇士，按照个人实力分为八个等级，和我国古代的官位品级一样，分为一品、二品、三品一直到八品。首领怕其他人不开心，所以将剩下的部落成员统一赋予九品官阶。

首领想要一统部落，必须先把大量的九品的子民们安顿好。眼看寒冬将至，以前的小木屋早已破烂不堪，首领决定给小弟们盖新房子，从九品开始，逐级往上，最后再给自己建造皇宫。

首领大人把建房计划安排好就打算尽快实施了。这时候又一个问题出现了，因为种族基因的问题，他们的部落人民完全不知道怎么计算数量。这就导致无法衡量建造一座木屋需要多少根木材，这时候首领有个大胆的想法，他找到了其中一位九品子民的小木屋，带着他的八位勇士充当了一次拆迁队。让这位九品子民和他的奴隶把木屋拆掉。然后源源不断的给八品勇士送去拆卸下来的木材，而八品勇士的任务是把收到的木材进行整理，当左右手各有一个的时候就把这两个木材绑起来送到七品勇士那里，七品勇士也是这样，满足左右手各一捆的时候，再把这两捆木材绑在一起，送给六品的勇士，以此类推，直到房屋被拆完，只有一品勇士手中有一大捆木材，其他勇士手中都空空如也。首领面对一脸迷茫的这位九品子民及其私有的奴隶，心中有了想要的结果。

这样首领就知道给九品子民建一座木屋只需要一品勇士手中的一捆木材。于是发动部落中所有九品子民和他们的奴隶，一起去旁边的空地划地分家。首领让每位九品子民按照适当间距排列站好，然后让奴隶们去森林中寻找木材，送到八品勇士手中，勇士之间还是按照拆木屋的方式收集木材，当一品勇士收集够一捆木材就堆放在一位九品子民身边，转到下一位九品子民处收集木材。直到最后每位九品子民身边都有了一捆木材，建木屋的准备工作就到此结束了，每位九品子民身旁的木材就刚好建一座木屋。

二进制工作机制故事——烽火告警

回到古代。你在一个烽火台上，我在另一个烽火台上，只要你那边来敌人，你就点狼烟通知我。这个能懂吧？

现在，我想清楚的知道你那儿来了几个敌人，我好做相应准备工作。怎么办呢？很简单，两个办法。

1、你点一次火，再灭掉一次，算是一个敌人，来两个就点2回，灭两回。我查点火的次数。

2、或者你同时点两堆火。我就知道，是来了两个敌人。我查点火的堆数。

你说要是一下来了200个敌人怎么办？你那边要么熏死，要么火堆多到足够自焚了，再说，那么多火堆，我一下也查不完……

时代在发展，人类在进步。一晃爱迪生来过地球了，他发明灯泡了。

你说可以用灯泡“亮”和“灭”来跟我表示这个信息。

如果一个灯泡没亮，说明没有敌人。因为灯泡没亮，也可以说是状态0。

如果来了一个敌人，灯泡亮了，我就知道来了1个，这就是状态1。

问题又来了，还是来了200个敌人……我去，要么你开关200次灯泡，要么准备200个灯泡一起亮。

第一个方法灯泡质量也不一定好，再说，你闪那么快，我还是数不过来。

第二个方法，我数也得数小半天，没数完，早被敌人冲过来砍死了。还有，200个灯泡，你确定你那儿电费余额够不？

好在咱们都是聪明人，咱们约定，多安装几个灯炮打暗号，不就行了。

为了不用画图，0代表关灯，1代表开灯。

00000000，8个灯全关，放心睡觉，这是状态0，说明一个敌人没有，平安无事。（状态0）换种说法，二进制和十进制的转换，只是“二进制在十进制里的编号位置”

00000001，这说明来了一个敌人，你负责干掉他就行了。叫状态1。

00000010，这是第二个能表示的状态，咱们给它个编号，叫状态2，说明来了两个敌人，也没啥大事。

接下来，应该是第三种情况了。00000011，这就是第三种情况。咱们不说换算什么的，这种亮灯的方法咱们就叫3（状态3）。

为了让咱俩都明白，咱们写个清单（文章最后）出来。由清单能看出来，如果来了255个敌人，你直接打开8个灯泡，我也就一目了然，准备刀枪就上了。

因为电脑也一样，信号线很多，但只有开和关（通电、断电）来表示两种状态（因为早期电子元件只能表达这两种状态），就采用“二进制”了，以至于N年以后电子元件能表示出第三种状态“三进制”的时候，二进制已经成为全世界的通用语言，地位无法撼动了。

二机制与十进制转换

bit(位)：数据存储的最小单元。在计算机二进制系统中，位，简记为b，也称为比特(bit)，每个二进制数字0或1就是一个位(bit)，其中每 8bit = 1 byte(字节)；

要从右到左用二进制的每个数去乘以2的相应次方（次方要从0开始算起）；

     假如：二进制数1101转化成十进制 ，那么 1101 = 1*20+0*21+1*22+1*23 = 1+0+4+8 = 13；

二进制运算----原码/反码/补码

对于有符号数而言：

  (1)二进制的最高位是符号位：0表示正数，1表示负数

  (2)正数的原码、反码、补码都一样；

  (3)负数的反码 =  它的原码符号位不变，其他位取反（0 ->1 ; 1->0 ）；

  (4)负数的补码 = 它的反码 +1；

  (5)0的反码、补码都是0；

  (6)***在计算机运算的时候，都是以补码的方式来运算的***；

  
  例子：

  下面我们就使用“有符号数”来模拟一下，在计算机中是怎样运算的。

  (1)正数相加：

       例如：1+1 ，在计算机中运算如下：

       1的原码为：

       00000000  00000000  00000000  00000001

       因为“正数的原码、反码、补码都一样”，所以，1的补码 = 1的原码，所以 1的补码+ 1的补码 就等于：

       00000000  00000000  00000000  00000001

       +

       00000000  00000000  00000000  00000001

       =

       00000000  00000000  00000000  00000010

       00000000  00000000  00000000  00000010（ 转换为10进制） = 0*2^0 + 1*2^1 = 0 + 2 =2 

  (2)正数相减：

       例如：1-2，在计算机中运算如下：

       在计算机中减运算其实是作为加运算来操作的，所以，1-2 = 1 + ( -2 )

       第一步：把 1补码找出来（因为正数的原码、反码、补码都一样，所以我们可通过原码直接获取补码）：

         1的补码：

         00000000   00000000   00000000   00000001

       第二步：把-2的原码找出来：

         -2的原码：

         10000000   00000000   00000000   00000010

       第三步：把-2的反码找出来：

         -2的反码：

         11111111     11111111     11111111     11111101

       第三步：把-2的补码找出来：

         -2的补码：

         11111111     11111111     11111111     11111110

       第四步：1的补码与-2的补码相加：

          00000000   00000000   00000000   00000001

          +

          11111111     11111111     11111111      11111110

          =

          11111111     11111111     11111111      11111111

       第五步：将计算结果的补码转换为原码，反其道而行之即可（如果想将二进制转换为十进制，必须得到二进制的原码）

          补码：11111111     11111111     11111111      11111111

          =

          反码：11111111     11111111     11111111      11111110

          =

          原码：10000000  00000000   00000000    00000001

      第六步：将计算结果的二进制原码 转换 为十进制

          二进制原码：10000000  00000000   00000000    00000001  =  1*2^0 =  -1

计算机基本原理

基本概念

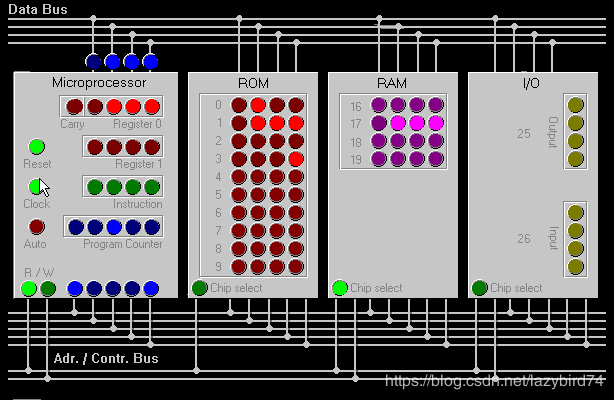
CPU的内部结构如下图所示：


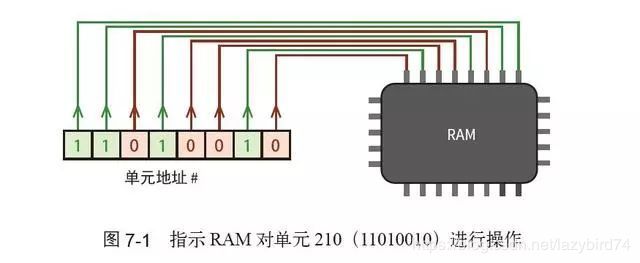
每条信号线传输一个比特，以高电压表示信号“1”，低电压表示信号“0”，如图7-1 所示。

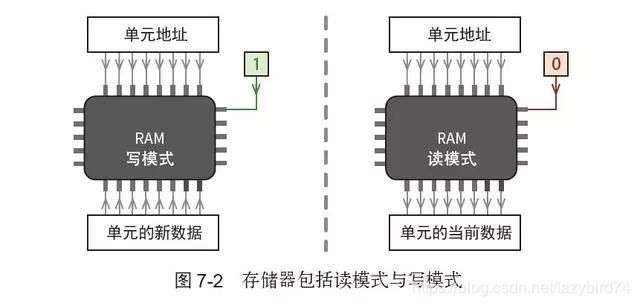
对于某个给定的单元地址，存储器可以进行两种操作：获取其值或存储新值，如图7-2 所示。存储器包括一条用于设置操作模式的特殊信号线。

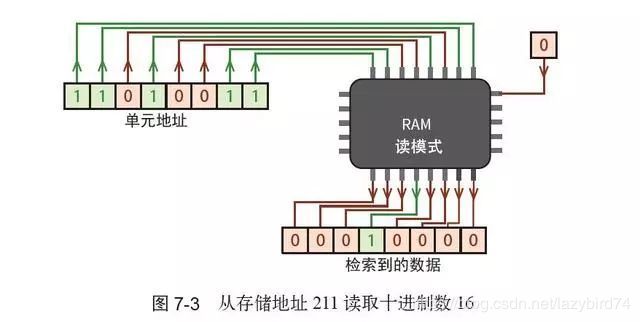
每个存储单元通常存储一个 8 位二进制数，它称为字节。设置为“读”模式时，存储器检索保存在单元中的字节，并通过8 条数据传输线输出，如图7-3 所示。

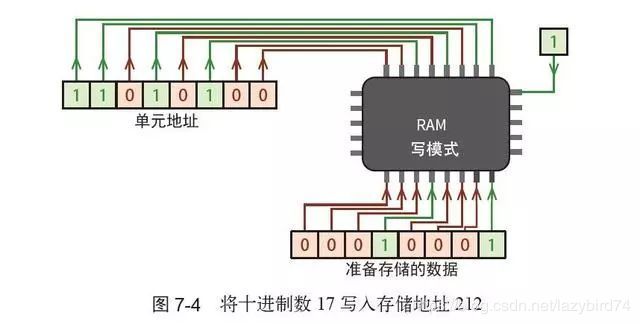
设置为“写”模式时，存储器从数据传输线获取一个字节，并将其写入相应的单元，如图7-4 所示。

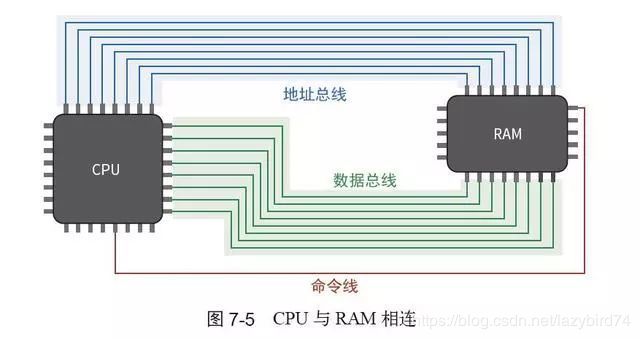
传输相同数据的一组信号线称为总线。用于传输地址的8 条信号线构成地址总线，用于在存储单元之间传输数据的另外8 条信号线构成数据总线。地址总线是单向的（仅用于接收数据），而数据总线是双向的（用于发送和接收数据）。

在所有计算机中，CPU 与RAM 无时无刻不在交换数据：CPU 不断从RAM 获取指令与数据，偶尔也会将输出与部分计算存储在RAM 中，如图7-5 所示。

四位计算机组成

概述

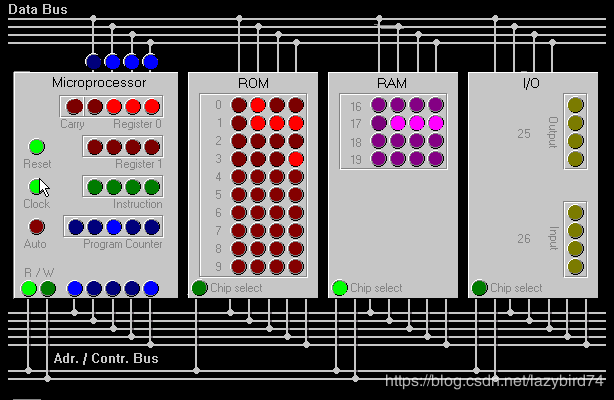
		以下是个4位的计算机组成，四位计算机主要运行存在ROM中的程序。 一个ROM的word宽是4位，意味着有2^4=16种装谈，支持16个指令集。
		指令分为两类：

• 一个字的命令：没有参数 两个字的命令：
• 需要一个参数（数据或地址），必须保存在ROM中
  程序写入ROM后，启动计算机，CPU会从ROM中的地址0的地方将指令取出，放到寄存器中， 这个过程叫“fetch”，取指令，接下来，指令执行，即“Execute”。
  处理一条指令需要多个时钟周期，在本例子中，执行一条指令的时钟周期定义如下：

. 1. a) 取指令阶段：4个时钟周期
- 将指令中ROM地址放到地址线上
- 将ROM中的程序命令放到数据线上/同时设置控制线的状态为READ
- 将程序命令写入到寄存中/同时解析指令（decode）
- 指针计数加1
-
1.b) 两字命令的第二次取指令：3个时钟周期
- 将ROM的地址放置到数据线上
- 将ROM地址中的参数放到数据总线上，并内部保存
- 指针计数加1

** 2. 执行阶段：1–3个时钟周期**
与执行的命令有关

组成说明

1 CPU, 包含如下内容：
R0: 一个4位的寄存器，溢出标志“carry”.
R1: 一个4位的寄存器，无溢出标志
IR: 指令寄存器，显示目前正在处理的指令
PC： 程序计数器，显示下一个待取指令的ROM地址。
Reset：除了ROM， RAM和IN
Clock：手动进入CPU时钟周期
Auto Knob： 确定CPU是否自动运行
2. ROM：
最大支持10个4位的程序命令
3. RAM
4个4位字大小空间
4. I/O
如果在IN元素，可以利用鼠标输入一个字，CPU能够从这里取。
OUT元素表示CPU已经将一个数字字放在了OUT端口
5. BUS
数据线：4位数据线用于组件之间的数据交换
地址线：5位，用于表示不同组件中的地址
控制线：2位，用于控制目前是读或写操作
在运行之前，必须在ROM中进行编程（通过点击上面的灯）。最后一条ROM指令执行完毕后，CPU自动跳回到ROM地址0处。

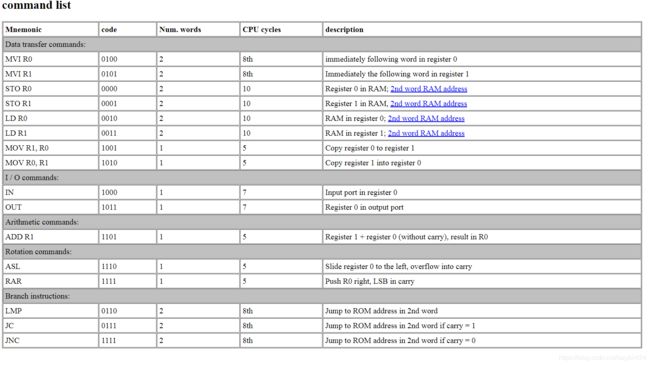
指令集

助记符	指令	参数大小（字数）	CPU周期	描述
MVI R0	0100	2	8	next word in register 0
MVI R1	0101	8
STO R0	0000	–	–
STO R1	0001	–	–
LD R0	0010	–	–
LD R1	0011	–	–
MOV R1, R0	1010	–	–
MOV RO, R1	1001	–	–
IN	1000	–	–
OUT	1011	–	–
ADD R1	1101	–	–
ASL	1110–	–	–
RAR	1111	–	–
LMP	0110	–	–
JC	0111	–	–
JNC	1111	–	–
–	–	–	–
–	–	–	–

RAM寻址：在例子中RAM的地址是16-19， 这些地址不能映射到4位中，所以在RAM中用0000-0011来表示RAM 16-19地址。

例子：
程序一：将R0中的一个字copy到RAM中的第二个地址（17）。

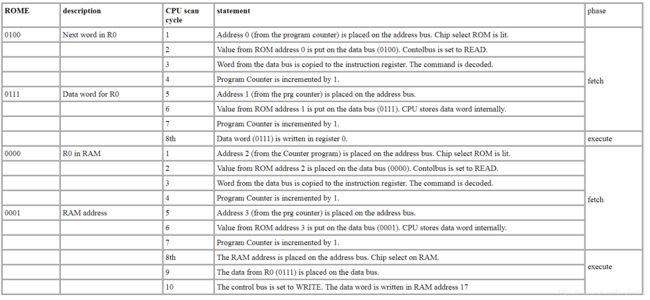
存储器的工作原理

存储1位的门电路图及说明

4个 NAND 门组成：

i是输入的bit，o是输出的bit，s是设置输出能否根据输入改变即该门能否有用的bit，真值表如下所示（G1表示1号NAND的输出,以此类推）：

s	i	a	b	c	o
1	1	0	1	0	1
1	0	1	0	1	0
0	1	1	1	0	保持上一个状态
0	0	0	1	0	保持上一个状态

从上述真值表中可以看出，当s为ON时，o=i；当s为OFF时，o保持i的上一个状态值。
综上：可以理解存储器通过s来实现对1位的某个时刻的状态进行保存，当s处于OFF时还能够保持。

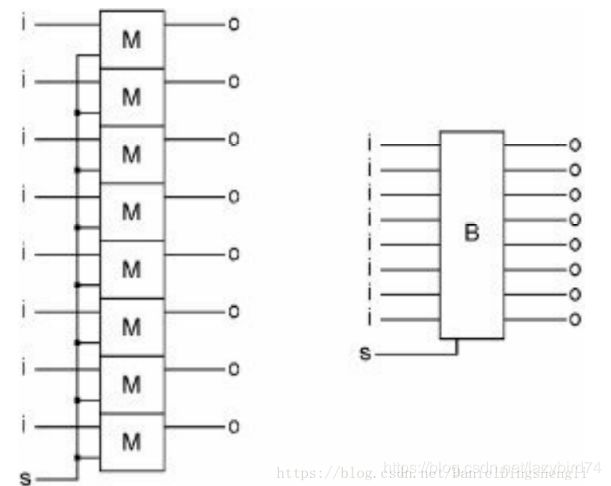
连接8个上述记忆门，记忆一个字节。

进一步地，为了一次性清除这8个输出位，我们可以将其与8个AND门（用E表示）连接，则E的开和关决定了B的输出，这就是一个寄存器的工作原理。

所有的寄存器都连接在总线上，当e使能时，该寄存器可以从总线上读写数据。

地址访问控制原理–地址译码器

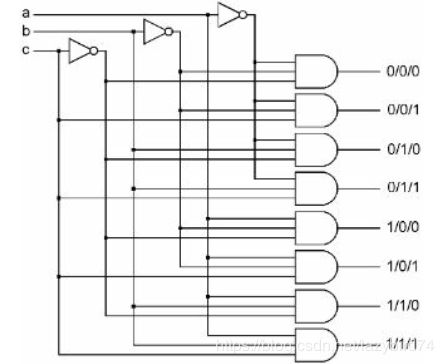
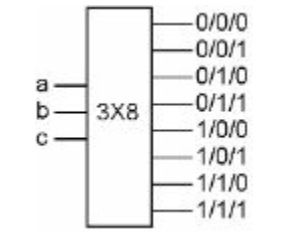
所有的存储单元都挂接在总线上，如何给定地址选中一个地址单元，向里面存储数据或者读取数据？这就需要用到地址译码器-decoder
原理：根据地址的输入，唯一地确定一个单元，看下面电路。

a	b	0/0	0/1	1/0	1/1
0	0	1	0	0	0
0	1	0	1	0	0
1	0	0	0	1	0
1	1	0	0	0	1

上述电路的特征：无论两路输入状态时什么，4个输出只有1位被选中（值为1），并且输入状态唯一决定了选中位（1）的位置。我们把输入ab看成是代码，这个电路可以将这个代码解读为选中某个位置。

进一步，扩展到3个代码，能够控制8个输出3*8

RAM存储器

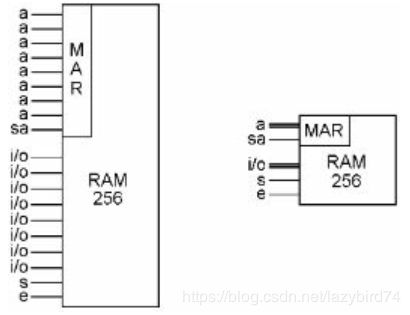
以丰巢储物柜为例，我们输入一个取件码，一个相应的柜子就打开了，其工作原理与存储器类似，每个存储单元与一个译码器（decoder）相连接，根据输入的取件码，唯一打开1个存储单元。

如下图所示，一个8位寄存器链接两个416的译码器，分别与行和列相连，sa用于控制寄存器R的输出，要么是0，要么是8位输入a。
1616个线共有256个交叉点，如前所述，每个译码器任何时刻只有1位选中（值为1），那么两个译码器将只有一个交叉点被选中（x1 && y1）.

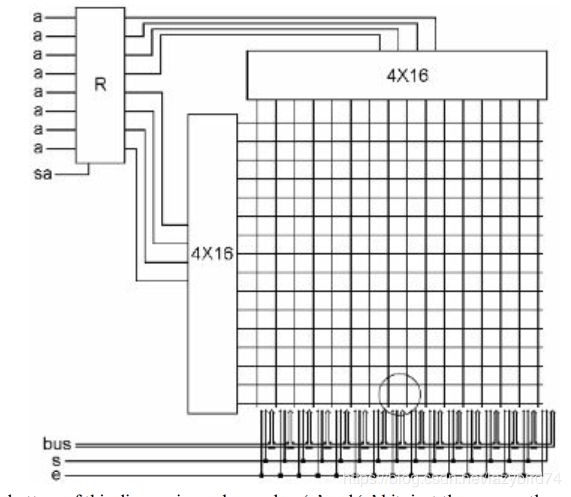
每个交叉点位置放置1个寄存器，寄存器的“s”位与“e”位与交叉点相连接，这样就能通过交叉点来控制寄存器了。对上面的交叉点进行放大，为下面的图示：

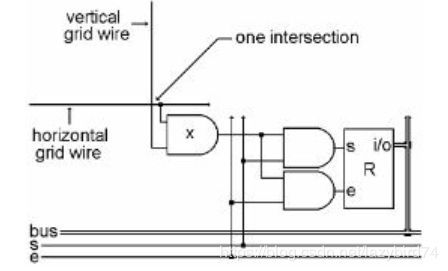
由上图看出，每个交叉点地方放置一个寄存器和3个 AND门， 寄存器与 数据线相连（bus）。
由于256个交叉点在任何时候只能有1个被选中（行列都为1），这样，256个寄存器在某一时刻只能有一个被选中用于读写（s和e是控制线）。如果x off，s和e位就会关闭，如果x on，则该寄存器选中，如果s=1，则可以写入R，如果e=1，在可以从R中读取。
上述就是计算机存储器的工作原理，由于可以随意访问任何一个存储单元，取名“Random Access Memory”, 简称RAM。
这个RAM， 使用了257个寄存器，256个寄存器是存储单元，1个寄存器用于选择存储单元的位置，这个地址寄存器叫地址寄存器（Memory Address Register，简称MAR）。

上述就是半个计算机了，主要有NAND门组成。

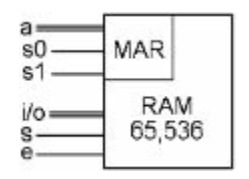
进一步地，如果要扩展内存，可以增加1个地址寄存器，利用2个8*256译码器，形成65536个地址单元：

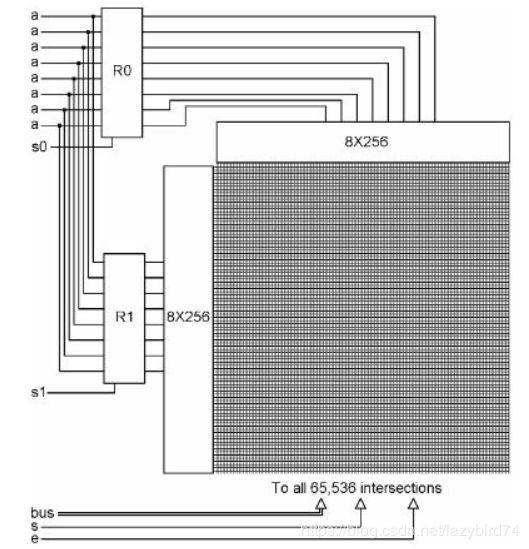
用下图简化表示：

计算机优化——更快

总线

分级存储

指令流水

IO