机器学习(三)-多元线性回归(数学推导及代码实现)
前面讨论了 y = ax + b 考虑的只有一个 特征值(因素)的情况下,但在很多情况下 特征值不只有一个 打个比方 要预测房价 要考虑的不只是面积 还要有 地段 建造年代 户型 等等 ,此时就要用到多元线性回归了。
( θ 0 , θ 1 , θ 2 , θ 3 , . . . . . , θ n ) (\theta_{0},\theta_{1},\theta_{2},\theta_{3},.....,\theta_{n}) (θ0,θ1,θ2,θ3,.....,θn) θ \theta θ代表一系列我们需要学习出来的参数
( 1 , X 1 ( i ) , X 2 ( i ) , X 3 ( i ) , . . . . . , X n ( i ) (1,X_{1}^{(i)},X_{2}^{(i)},X_{3}^{(i)},.....,X_{n}^{(i)} (1,X1(i),X2(i),X3(i),.....,Xn(i) X代表了要训练的参数(特征) 比如 面积 朝向 户型 装修 交通 等等特征
决定一间房屋的价格可以由很多因素综合的出 这一组综合的权重就是要求解得出的。
房屋价格 = 面积*面积的权重 + 朝向 * 朝向的权重 + 户型 * 户型的权重 + 装修 * 装修的权重 + 交通 * 交通的权重
y ^ ( i ) = θ 0 X 0 ( i ) + θ 1 X 1 ( i ) + θ 2 X 2 ( i ) + θ 3 X 3 ( i ) , . . . . . , θ n X n ( i ) \hat{y}^{(i)} =\theta_{0}X_{0}^{(i)}+\theta_{1}X_{1}^{(i)}+\theta_{2}X_{2}^{(i)}+\theta_{3}X_{3}^{(i)},.....,\theta_{n}X_{n}^{(i)} y^(i)=θ0X0(i)+θ1X1(i)+θ2X2(i)+θ3X3(i),.....,θnXn(i)
此处 θ 0 X 0 ( i ) \theta_{0}X_{0}^{(i)} θ0X0(i) =b 为偏置(截距)
y ^ ( i ) = b + θ 1 X 1 ( i ) + θ 2 X 2 ( i ) + θ 3 X 3 ( i ) , . . . . . , θ n X n ( i ) \hat{y}^{(i)} =b+\theta_{1}X_{1}^{(i)}+\theta_{2}X_{2}^{(i)}+\theta_{3}X_{3}^{(i)},.....,\theta_{n}X_{n}^{(i)} y^(i)=b+θ1X1(i)+θ2X2(i)+θ3X3(i),.....,θnXn(i)
使用和一元线性同样的 损失函数:
a r g m i n ∑ i = 1 m ( y ( i ) − y ^ ( i ) ) 2 {argmin}\sum_{i=1}^{m}(y^{(i)} - \hat{y}^{(i)})^2 argmin∑i=1m(y(i)−y^(i))2
写成矩阵形式
θ = ( θ 0 , θ 1 , θ 2 , θ 3 , . . . . . , θ n ) T \theta=(\theta_{0},\theta_{1},\theta_{2},\theta_{3},.....,\theta_{n})^T θ=(θ0,θ1,θ2,θ3,.....,θn)T
X ( i ) = ( 1 , X 1 ( i ) , X 2 ( i ) , X 3 ( i ) , . . . . . , X n ( i ) ) T X^{(i)}=(1,X^{(i)}_{1},X^{(i)}_{2},X^{(i)}_{3},.....,X^{(i)}_{n})^T X(i)=(1,X1(i),X2(i),X3(i),.....,Xn(i))T
方程于是就变成:
y ^ ( i ) = θ ⋅ X ( i ) \hat y^{(i)} =\theta \cdot X^{(i)} y^(i)=θ⋅X(i)
相当于 y = θ X + b y=\theta X + b y=θX+b 的矩阵形式
输入的样本:
X = [ 1 X ( 1 ) ( 1 ) X ( 2 ) ( 1 ) . . . . X ( n ) ( 1 ) 1 X ( 1 ) ( 2 ) X ( 2 ) ( 2 ) . . . . X ( n ) ( 2 ) . . . . . 1 X ( 1 ) ( m ) X ( 2 ) ( m ) . . . . X ( n ) ( m ) ] X = \left[ \begin{matrix} 1 & X^{(1)}_{(1)} & X^{(1)}_{(2)} & .... & X^{(1)}_{(n)}\\ 1 & X^{(2)}_{(1)} & X^{(2)}_{(2)} & .... & X^{(2)}_{(n)}\\ ..... \\1 & X^{(m)}_{(1)} & X^{(m)}_{(2)} & .... & X^{(m)}_{(n)}\\ \end{matrix} \right] X=⎣⎢⎢⎢⎡11.....1X(1)(1)X(1)(2)X(1)(m)X(2)(1)X(2)(2)X(2)(m)............X(n)(1)X(n)(2)X(n)(m)⎦⎥⎥⎥⎤
待求得权重: θ = [ θ 0 θ 1 θ 2 . . . . θ n ] T \theta = \left[ \begin{matrix} \theta_{0} \\ \theta_{1} \\ \theta_{2} \\....\\\theta_{n} \\\end{matrix} \right]^T θ=⎣⎢⎢⎢⎢⎡θ0θ1θ2....θn⎦⎥⎥⎥⎥⎤T 真实值: y = [ y 0 y 1 y 2 . . . . y n ] y = \left[ \begin{matrix} y_{0} \\ y_{1} \\ y_{2} \\....\\y_{n} \\\end{matrix} \right] y=⎣⎢⎢⎢⎢⎡y0y1y2....yn⎦⎥⎥⎥⎥⎤
X 为 m ∗ ( n + 1 ) 的 矩 阵 X 为m*(n+1)的矩阵 X为m∗(n+1)的矩阵
θ 为 ( n + 1 ) ∗ 1 列 的 向 量 \theta为 (n+1) * 1 列的向量 θ为(n+1)∗1列的向量
y 为 ( n + 1 ) ∗ 1 列 的 向 量 y 为 (n+1) * 1 列的向量 y为(n+1)∗1列的向量
下标(n) 代表特征(参数)数量
上表(m)代表 训练数据数量
X 第一列 为1 相当于 θ \theta θ为 偏置 b
a r g m i n ∑ i = 1 m ( y ( i ) − y ^ ( i ) ) 2 {argmin}\sum_{i=1}^{m}(y^{(i)} - \hat{y}^{(i)})^2 argmin∑i=1m(y(i)−y^(i))2 → a r g m i n ( Y − X ⋅ θ ) 2 {argmin}(Y -X \cdot \theta)^2 argmin(Y−X⋅θ)2 → a r g m i n ( Y − X ⋅ θ ) T ⋅ ( Y − X ⋅ θ ) {argmin}(Y - X \cdot \theta )^T \cdot(Y - X\cdot \theta ) argmin(Y−X⋅θ)T⋅(Y−X⋅θ)
所以 问题就转化成 求上述式子的最小值,求最小值是一个凸优化问题 遇到这种问题 一般 先需要证明 这个式子是有凸函数连续可导。
(以下推导可以不看 直接看结论)
一般推导思路
凸集定义
设集合 D ⊂ R n D \subset R^n D⊂Rn,如果对集合内任意元素 x , y ⊂ D x,y \subset D x,y⊂D与任意的 a ⊂ [ 0 , 1 ] a \subset [0,1] a⊂[0,1],有 a x + ( 1 − a ) y ⊂ D ax + (1 - a)y \subset D ax+(1−a)y⊂D,则称集合D是凸集。
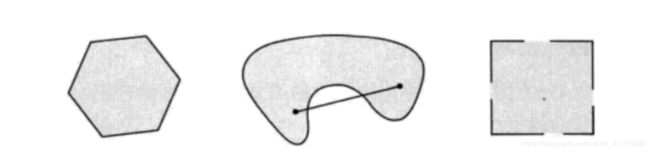
任意连2条直线 所形成的集合还在原空间中则称为凸集。
梯度定义
设n原函数 f ( x ) f(x) f(x) 对自变量 x = ( x 1 , x 2 , . . . , x n ) T x = (x_1,x_2,...,x_n)^T x=(x1,x2,...,xn)T的个分量 x i x_i xi的偏导数 ∂ f ( x ) ∂ x i i = ( 1 , 2 , 3... , n ) \frac {\partial f(x)}{\partial x_i} i=(1,2,3...,n) ∂xi∂f(x)i=(1,2,3...,n)都存在,则函数 f(x)在x处一阶可导,并称向量
∇ f ( x ) = [ ∂ f ( x ) ∂ x 1 ∂ f ( x ) ∂ x 2 . . . ∂ f ( x ) ∂ x n ] \nabla f(x) = \left[ \begin{matrix} \frac {\partial f(x)}{\partial x_1} \\ \frac {\partial f(x)}{\partial x_2} \\ ... \\ \frac {\partial f(x)}{\partial x_n} \end{matrix} \right] ∇f(x)=⎣⎢⎢⎢⎡∂x1∂f(x)∂x2∂f(x)...∂xn∂f(x)⎦⎥⎥⎥⎤
为函数 f ( x ) f(x) f(x)在x处的一节阶倒数或梯度,记为 ∇ f ( x ) \nabla f(x) ∇f(x)(列向量)
海塞矩阵
Hession(海塞)矩阵定义:设n元函数 f ( x ) f(x) f(x)对自变量 x = ( x 1 , x 2 , . . . . , x n ) T x =(x_1,x_2,....,x_n)^T x=(x1,x2,....,xn)T的各分量 x i x_i xi的二阶偏导数 ∂ 2 f ( x ) ∂ x i ∂ x j ( i , j = 1 , 2 , 3..... , n ) \frac{\partial ^2f(x)}{\partial x_i \partial x_j}(i,j = 1,2,3.....,n) ∂xi∂xj∂2f(x)(i,j=1,2,3.....,n)都存在,则称函数 f ( x ) f(x) f(x)在点 x x x处二阶可导,并称矩阵
∇ 2 f ( x ) = ∇ f ( x ) = [ ∂ 2 f ( x ) ∂ x 1 2 ∂ 2 f ( x ) ∂ x 1 ∂ x 2 . . . ∂ 2 f ( x ) ∂ x 1 ∂ x n ∂ 2 f ( x ) ∂ x 2 ∂ x 1 ∂ 2 f ( x ) ∂ x 2 2 . . . ∂ 2 f ( x ) ∂ x 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ 2 f ( x ) ∂ x n ∂ x 1 ∂ 2 f ( x ) ∂ x n ∂ x 2 . . . ∂ 2 f ( x ) ∂ x n ∂ x n ] \nabla ^2 f(x) = \nabla f(x) = \left[ \begin{matrix} \frac {\partial ^2 f(x)}{\partial x_1^2 } & \frac {\partial ^2 f(x)}{\partial x_1 \partial x_2 } & ... & \frac {\partial ^2 f(x)}{\partial x_1\partial x_n} \\ \frac {\partial ^2 f(x)}{\partial x_2 \partial x_1} & \frac {\partial ^2 f(x)}{\partial x_2^2 } & ... & \frac {\partial ^2 f(x)}{\partial x_2\partial x_n} \\ \vdots & \vdots& \ddots & \vdots \\ \frac {\partial ^2 f(x)}{\partial x_n \partial x_1 } & \frac {\partial ^2 f(x)}{\partial x_n \partial x_2 } & ... & \frac {\partial ^2 f(x)}{\partial x_n\partial x_n} \end{matrix} \right] ∇2f(x)=∇f(x)=⎣⎢⎢⎢⎢⎢⎡∂x12∂2f(x)∂x2∂x1∂2f(x)⋮∂xn∂x1∂2f(x)∂x1∂x2∂2f(x)∂x22∂2f(x)⋮∂xn∂x2∂2f(x)......⋱...∂x1∂xn∂2f(x)∂x2∂xn∂2f(x)⋮∂xn∂xn∂2f(x)⎦⎥⎥⎥⎥⎥⎤
为 f ( x ) f(x) f(x)在 x x x处的二阶倒数或 Hession 矩阵 ,记为 ∇ 2 f ( x ) \nabla ^2 f(x) ∇2f(x),若 f ( x ) f(x) f(x)对 x x x 各变元的所有二阶偏导数都连续,则 ∂ 2 f ( x ) ∂ x i x j \frac{\partial ^2f(x)}{\partial x_ix_j} ∂xixj∂2f(x) = ∂ 2 f ( x ) ∂ x j x i \frac{\partial ^2f(x)}{\partial x_jx_i} ∂xjxi∂2f(x)
多元实值函数凹凸型判定定理
设 D ⊂ R n D \subset R^n D⊂Rn是非空开凸集, f : D ⊂ R n , f:D \subset R^n , f:D⊂Rn,且 f ( x ) f(x) f(x)在 D D D上二阶连续可微,如果 f ( x ) f(x) f(x)的Hession矩阵 ∇ 2 f ( x ) \nabla ^2 f(x) ∇2f(x)在 D D D上是正定的,则 f ( x ) f(x) f(x)是D上的严格凸函数。
凸充分性定理
若$f:R^n → R $ 是凸函数,且 f ( x ) f(x) f(x)一阶连续可微,则 x ∗ x^* x∗是全局最优解(全局最小值)的充分必要条件是 ∇ f ( x ∗ ) = 0 \nabla f(x ^*) = 0 ∇f(x∗)=0,其中 f ( x ) f(x) f(x)关于 x x x的一阶导数(也称梯度)
[标量-向量]的矩阵微分公式为:
∂ y ∂ x = ( ∂ y ∂ x 1 ∂ y ∂ x 2 ⋮ ∂ y ∂ x n ) \frac{\partial y}{\partial x} = \left(\begin{matrix} \frac{\partial y}{\partial x_1} \\ \frac{\partial y}{\partial x_2} \\ \vdots \\ \frac{\partial y}{\partial x_n} \end{matrix} \right) ∂x∂y=⎝⎜⎜⎜⎜⎛∂x1∂y∂x2∂y⋮∂xn∂y⎠⎟⎟⎟⎟⎞
( 分 母 布 局 ) (分母布局) (分母布局)
∂ y ∂ x = ( ∂ y ∂ x 1 ∂ y ∂ x 2 … ∂ y ∂ x n ) \frac{\partial y}{\partial x} = \left(\begin{matrix} \frac{\partial y}{\partial x_1} \frac{\partial y}{\partial x_2} \ldots \frac{\partial y}{\partial x_n} \end{matrix} \right) ∂x∂y=(∂x1∂y∂x2∂y…∂xn∂y)
( 分 子 布 局 ) (分子布局) (分子布局)
其中, x = ( x 1 , x 2 , . . . . . , x n ) T x =(x_1,x_2,.....,x_n)^T x=(x1,x2,.....,xn)T为n为向量, y y y为 x x x的 n n n元标量函数.
分子分母布局按照习惯选择。
由[标量 -向量]的矩阵微分公式可推得:
∂ x T a ∂ x = ∂ a T x ∂ x \frac {\partial x^Ta}{\partial x} =\frac {\partial a^T x}{\partial x} ∂x∂xTa=∂x∂aTx = ∂ y ∂ x = ( ∂ ( a 1 x 1 + a 2 x 2 + . . . + a n x n ) ∂ x 1 ∂ ( a 1 x 1 + a 2 x 2 + . . . + a n x n ) ∂ x 2 ⋮ ∂ ( a 1 x 1 + a 2 x 2 + . . . + a n x n ) ∂ x n ) \frac{\partial y}{\partial x} = \left(\begin{matrix} \frac{\partial (a_1x_1 + a_2x_2 +...+a_nx_n)}{\partial x_1} \\ \frac{\partial (a_1x_1 + a_2x_2 +...+a_nx_n)}{\partial x_2} \\ \vdots \\ \frac{\partial (a_1x_1 + a_2x_2 +...+a_nx_n)}{\partial x_n} \end{matrix} \right) ∂x∂y=⎝⎜⎜⎜⎜⎛∂x1∂(a1x1+a2x2+...+anxn)∂x2∂(a1x1+a2x2+...+anxn)⋮∂xn∂(a1x1+a2x2+...+anxn)⎠⎟⎟⎟⎟⎞= ( a 1 a 2 ⋮ a n ) \left(\begin{matrix} a_1\\a_2 \\ \vdots \\a_n \end{matrix} \right) ⎝⎜⎜⎜⎛a1a2⋮an⎠⎟⎟⎟⎞=a
同理可推得: ∂ x T B x ∂ x = ( B + B T ) x \frac{\partial x^TBx}{\partial x} =(B +B^T)x ∂x∂xTBx=(B+BT)x
有了以上定理就可以开始证明了:
- 证明损失函数 E θ E\theta Eθ 是关于 θ \theta θ的凸函数。
∂ E θ ∂ θ = ∂ ( ( Y − X ⋅ θ ) T ( Y − X ⋅ θ ) ) ∂ θ \frac{\partial E \theta}{\partial \theta }=\frac{\partial(( Y- X \cdot \theta)^T (Y - X \cdot \theta ))}{\partial \theta} ∂θ∂Eθ=∂θ∂((Y−X⋅θ)T(Y−X⋅θ))
= ∂ ∂ θ ( Y − θ T X T ) ( Y − X θ ) \frac{\partial}{\partial \theta}( Y-\theta ^T X^T) (Y - X \theta) ∂θ∂(Y−θTXT)(Y−Xθ)
= ∂ ∂ θ [ − Y T X θ − θ T X T Y + θ T X T X θ ] \frac{ \partial}{\partial \theta}[-Y^TX\theta - \theta^TX^TY + \theta^TX^TX\theta] ∂θ∂[−YTXθ−θTXTY+θTXTXθ]
= ∂ Y T X θ ∂ θ − ∂ θ T X T Y ∂ θ + ∂ θ T X T X θ ∂ θ \frac{ \partial Y^TX \theta}{\partial \theta} -\frac{ \partial \theta ^T X^TY}{\partial \theta} +\frac{ \partial \theta^TX^TX\theta}{\partial \theta} ∂θ∂YTXθ−∂θ∂θTXTY+∂θ∂θTXTXθ
由 ∂ x T a ∂ x = ∂ a T x ∂ x \frac {\partial x^Ta}{\partial x} =\frac {\partial a^T x}{\partial x} ∂x∂xTa=∂x∂aTx = ∂ y ∂ x = a \frac{\partial y}{\partial x} =a ∂x∂y=a ∂ x T B x ∂ x = ( B + B T ) x \frac{\partial x^TBx}{\partial x} =(B +B^T)x ∂x∂xTBx=(B+BT)x可得:
∂ E θ ∂ θ = − X T y − X T y + ( X T X + X T X θ ) \frac{\partial E_\theta}{\partial\theta} = -X^Ty -X^Ty +(X^TX +X^TX\theta) ∂θ∂Eθ=−XTy−XTy+(XTX+XTXθ)
= 2 X T ( X θ − Y ) 2X^T(X\theta - Y) 2XT(Xθ−Y) 为一阶偏导
再对一阶偏导数求二阶偏导数:
∂ 2 E θ ∂ θ ∂ θ T \frac {\partial ^2E \theta}{\partial \theta\partial \theta^T} ∂θ∂θT∂2Eθ = ∂ ∂ θ ( ∂ E θ ∂ θ ) \frac{\partial }{\partial \theta}(\frac{\partial E \theta}{\partial \theta}) ∂θ∂(∂θ∂Eθ) = ∂ ∂ E θ ( 2 X T X θ − 2 X T Y ) \frac{\partial}{\partial E \theta}(2X^TX\theta - 2X^TY) ∂Eθ∂(2XTXθ−2XTY)= 2 X T X 2X^TX 2XTX (即Hession矩阵)
假设 X T X X^TX XTX为正定矩阵( E θ E\theta Eθ 是关于 θ \theta θ的凸函数)
令 E θ E\theta Eθ 关于 θ \theta θ的一阶导数为0 前面已经证明过了:
∂ E θ ∂ θ \frac{\partial E \theta}{\partial \theta } ∂θ∂Eθ= 2 X T ( X θ − Y ) = 0 2X^T(X\theta - Y)=0 2XT(Xθ−Y)=0
2 X T X θ − 2 X T Y = 0 2X^TX\theta - 2X^TY =0 2XTXθ−2XTY=0
2 X T X θ = 2 X T Y 2X^TX\theta = 2X^TY 2XTXθ=2XTY
2边除以2:
X T X θ = X T Y X^TX\theta = X^TY XTXθ=XTY
2边乘以 ( X T X ) − 1 (X^TX)^{-1} (XTX)−1
( X T X ) − 1 X T X θ = ( X T X ) − 1 X T Y (X^TX)^{-1}X^TX\theta = (X^TX)^{-1}X^TY (XTX)−1XTXθ=(XTX)−1XTY
得: θ = ( X T X ) − 1 X T Y \theta = (X^TX)^{-1}X^TY θ=(XTX)−1XTY
以上证明毕:
θ = ( X T X ) − 1 X T Y \theta = (X^TX)^{-1}X^TY θ=(XTX)−1XTY
问题:时间复杂度高:O( n 3 n^3 n3)(优化后O( n 2.4 n^{2.4} n2.4)
优点:不需要对数据做归一化处理
import numpy as np
class LinearRegression:
def __init__(self):
"""初始化linear Regression模型"""
self.coef_ = None
self.interception_ = None
self._theta = None
def fit_normal(self,X_train,y_train):
assert X_train.shape[0] == y_train.shape[0], \
"the size of x_train must be equal to the size of y_train"
#传入的训练样本没有截距 在每一行加一个截距项
X_b = np.hstack([np.ones((len(X_train),1)),X_train])
#根据公式计算 theta 的值
self._theta = np .linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
self.interception_=self._theta[0]
self.coef_ = self._theta[1:]
return self
def predict(self,X_predict):
assert self.coef_ is not None and self.interception_ is not None, \
"you must run fit_normal before predict"
assert X_predict.shape[1] == len(self.coef_), \
"the size of X_predict must be equal to the size of X_train"
X_predict_b = np.hstack([np.ones((len(X_predict),1)), X_predict])
return X_predict_b.dot(self._theta)
def score(self, X_test,y_test):
y_predict = self.predict(X_test)
return r_Squared(y_test,y_predict)
def __repr__(self):
return "LinearRegression()"
def r_Squared(y_true,y_predict):
assert len(y_true) == len(y_predict), \
"the size of y_true must be equal to the size of y_predict"
return 1- (mean_squared_error(y_true,y_predict) / np.var(y_true))
测试
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from ml_utils.data_split import train_test_split
from sklearn import datasets
boston = datasets.load_boston()
x = boston.data
y = boston.target
reg = LinearRegression()
reg.fit_normal(x_train,y_train)
print(reg.coef_)
print(reg.interception_)
print(reg.score(x_test,y_test))
Sklearn中的线性回归
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
boston = datasets.load_boston()
x =boston.data
y = boston.target
x_train,x_test,y_train,y_test = train_test_split(x,y,random_state=666);
lin_reg = LinearRegression()
lin_reg.fit(x_train,y_train)
#查看训练的权重参数
lin_reg.coef_
#截距
lin_reg.intercept_
#评分
lin_reg.score(x_test,y_test)

通过线性模型能找到 特征 比如 RM 是权重最高的 说明房间数量 和 房价正相关 而且 权重较高 CHAS 第二高的权重 表示 波士顿房子邻河不临河 临河和房价 也是正相关 而排在最后一个的参数 NOX 表示一氧化氮 的含量 和房价负相关 。这也说明线性回归法 对数据有可解释性 不管模型预测好坏 先用线性模型进行预测 能直观的观测处数据中存在的规律。
