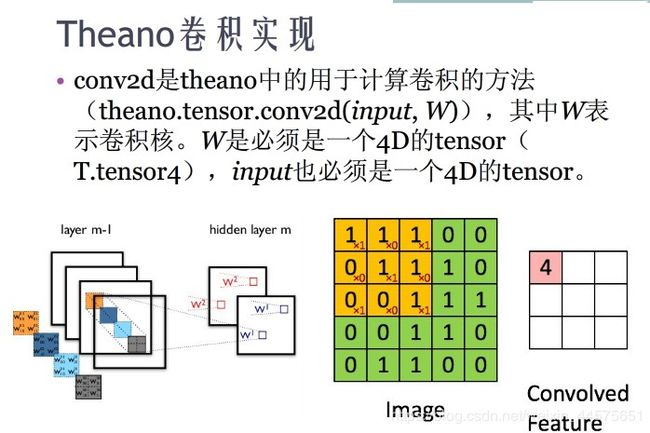
关于深度学习人工智能模型的探讨（八）（2）

8.2 卷积神经网络

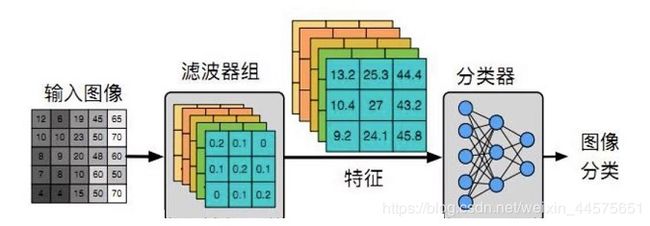
卷积神经网络(CNN)是深度学习模型的典型代表，在AI图像识别领域广泛应用。

CNN较一般神经网络在图像处理方面有如下优点：

a）特征要素提取相对容易；

b）逐层特征属性构建相对简单；

c）各层次特征复合匹配效果相对较好。

以图片识别的卷积神经网络为例:

C1层是一个卷积层，由6个Feature Map特征图构成。C1层特征图中每个神经元与输入中55的邻域相连。C1层特征图的大小为2828像素。C1有156个可训练参数[每个滤波器55=25个unit普通参数和一个bias偏置参数，一共6个卷积核滤波器，共(55+1)6=156个参数]，所以共有156(28*28)=122304个连接。

S2层是一个子采样层，有6个1414像素的特征图。特征图中的每个单元与C1中相对应特征图的22邻域相连接。S2层每个单元的4个输入相加，乘以一个可训练u参数，再加上一个可训练b偏置。结果通过sigmoid函数计算。可训练系数和偏置控制着sigmoid函数的非线性程度。如果系数比较小，那么运算近似于线性运算，亚采样相当于模糊图像。如果系数比较大，根据偏置的大小亚采样可以被看成是有噪声的“或”运算或者有噪声的“与”运算。每个单元的2*2感受野并不重叠，因此S2中每个特征图的大小是C1中特征图大小的1/4（行和列各1/2）。S2层有12个可训练参数和5880个连接。

然后，每一隐层与隐层之间空间分辨率递减，而每层所含的平面数递增，这样可用于检测更多的特征信息。

C3层是下一个卷积层，它同样通过5x5的卷积核去卷积层S2的的特征图，然后得到的特征图只有10x10个像素，但是它有16种不同的卷积核，所以就存在16个特征图。这里需要注意的一点是：C3中的每个特征map是连接到S2中的所有6个或者几个特征map的，表示本层的特征map是上一层提取到的特征map的不同组合。

S4层是下一个子采样层，由16个55大小的特征图构成。特征图中的每个单元与C3中相应特征图的22邻域相连接，跟C1和S2之间的连接一样。S4层有32个可训练参数（每个特征图1个因子和一个偏置）和2000个连接。

C5层又是一个卷积层，有120个特征图。每个单元与S4层的全部16个单元的55邻域相连。由于S4层特征图的大小也为55像素，同卷积核滤波器一样大小，故C5特征图的大小为1*1：这构成了S4和C5之间的全连接。C5层有48120个可训练连接。

F6层有84个单元，与C5层全相连。有10164个可训练参数。F6层计算输入向量和权重向量之间的点积，再加上一个偏置。然后将其传递给sigmoid函数产生单元i的一个输出状态。

卷积神经网络是一个多层的神经网络，每层由多个二维平面组成，而每个平面由多个独立神经元组成。卷积后在C1层产生三个特征映射图，然后特征映射图中每组的四个像素再进行求和，加权值，加偏置，通过一个Sigmoid函数得到三个S2层的特征映射图。这些映射图再进过滤波得到C3层。这个层级结构再和S2一样产生S4。最终，并连接成一个向量输入到传统的神经网络，得到输出。

综上所述，卷积神经网络(CNN)的核心机制在于两点：

 第一，通过‘卷积滤波器’提取特征属性；

 第二，在多个隐层提取不同层次特征属性。

第一，通过‘卷积滤波器’提取特征属性；

卷积模块的本质作用就是通过‘卷积滤波器’凸出特征结构，从而提取到其主要特征要素：

RAM是输入图片，Buffer是feature map

卷积过程：用一个可训练的卷积滤波器fx去卷积一个输入的图像（第一阶段是输入的原始图像，后面的阶段就是上一层经过卷积处理过的卷积特征map了），然后加一个偏置bx，得到卷积层Cx。

也就是说，‘卷积滤波器’和feature map（特征属性）是相生相伴的：

第二，在多个隐层提取不同层次特征属性。

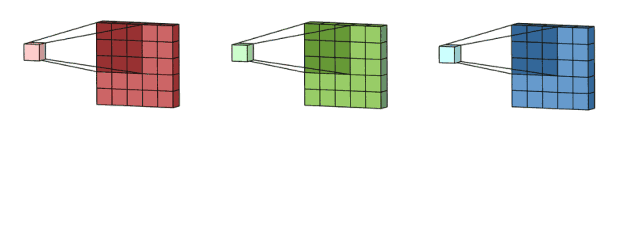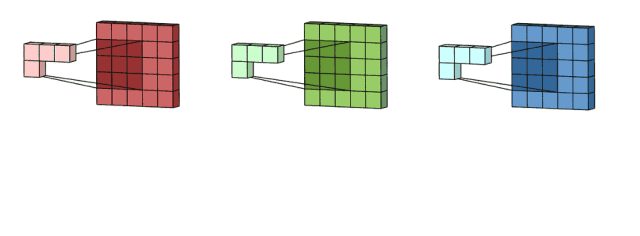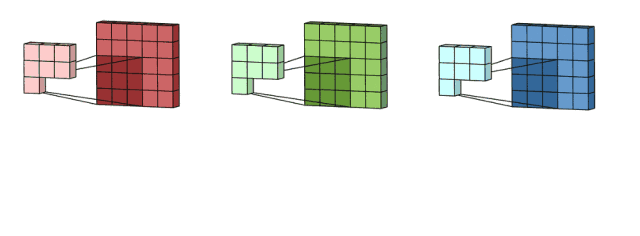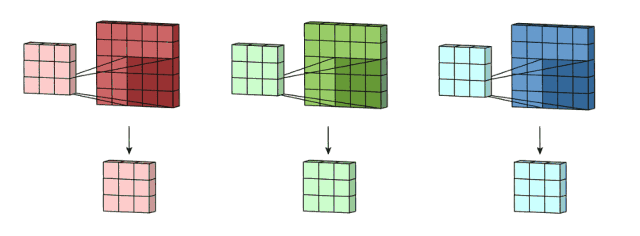
通过卷积神经网络感受野(receptive fiel)调整原始图像的像素点区域大小，映射不同大小区域的特征结构（feature map），从而提取不同层次的特征结构，构建不同层次的特征隐层。

机器学习系统的感受野(receptive field)通过伸缩范围框定不同大小的像素区域，建立不同特征粒度的多个层次的隐层,比如第一个隐层框定100x100像素feature map，第二个隐层框定200x200像素feature map、第三个隐层框定300x100像素feature map,第四个隐层框定100x200像素feature map、第五个隐层框定50x300像素feature map…这样，原本一张原始平面图片被一层又一层特征隐层扩张成了多层次特征属性的高阶逻辑张量模型。

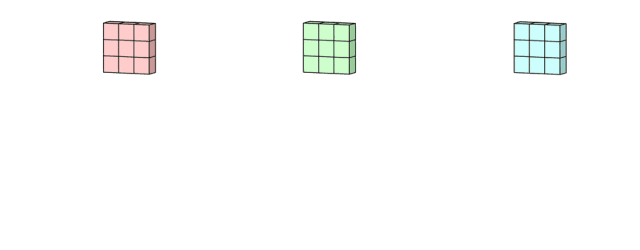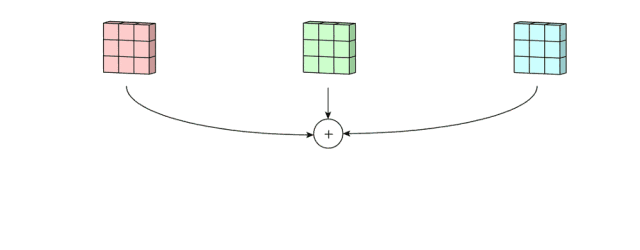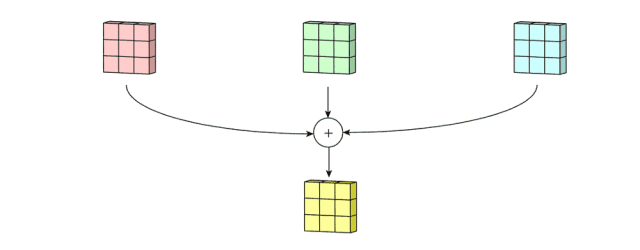
然后，将不同隐层feature map进行特征属性复合：

其中Op是输出，Xp是样本输入，Fn是滤波功能函数，W（n）是加权参数

非常有意思的现象是，无论是CV(计算机视觉)、或是NLP(自然语言处理)模型，有效的卷积神经网络特征属性分析系统，往往有更深的结构(很多层的隐层），而不是更胖（一层的参数很多）。

为什么会这样呢？

首先，如果各个特征结构放在同一层，等效于一个线性空间参照系。歌德尔不完备性定理论证了线性空间参照系的局限性。基于线性空间参照系的人工智能研究沉寂了半个世纪，也充分说明了单层特征结构的局限性。

其次，实践证明，卷积神经网络在实际应用中，把卷积滤波器加入一层又一层的隐层中，而不是在一层分析中添加太多的特征基，效果往往好得多。

难免有人好奇，为什么卷积滤波器的层次要做得很深，而不是很胖。换句话说，为什么非得把特征基放到很多不同的隐层中呢？ 为什么在同一层隐层里面配置很多个特征基效果并不好呢？

直观的解释是，更深层的结构，可以提取到不同层次的特征抽象，从而更有利于匹配特征属性：

和卷积神经网络一样，所有的深度学习模型的根本要点在于两个方面：

1、提取一个层次的特征基系，线性组合之，相当于加法：S =∑an

2、在多个隐层提取不同层次特征基系，逐层复合之，相当于乘法：f1(f2(f3(x)))= f1f2f3

以数学眼光而言，深度学习模型的多层次线性关系意味着（n阶a维）高阶张量，其（a的n次方维）表象空间（n趋于阿列夫1阶无穷大时，a的n次方维即阿列夫2阶无穷大维）远远超越了平面矩阵的特征属性表达范围局限（阿列夫1维）。

深度学习模型相当于n阶m维张量（即‘m的n次方’特征维度），n表示隐层的层数，m表示每一层的特征参数。更深的结构意味着n比m多，而更胖的结构意味着m比n多。

显然， 更深的结构时的‘m的n次方’特征维度，意味着更完备的特征表达（n趋于阿列夫1阶无穷大时，m的n次方维意味着阿列夫2维）。

另一方面， 更胖的结构时的‘m的n次方’特征维度，意味着少得多的特征属性（m趋于阿列夫1阶无穷大时，m的n次方维还是阿列夫1维）。

同样地道理，可以解释为什么四维闵氏空间复合而成的广义相对论是确定的，而连续无穷维傅立叶谱分析的量子力学却表现为不确定性：

广义相对论的n阶4维张量是‘4维的n次方’特征维度黎曼流形（n趋于阿列夫1阶无穷大时，‘4维的n次方’意味着阿列夫2维特征基），阿列夫2阶无穷大特征维度是完备的张量空间，所以广义相对论是确定的。

量子力学的连续无穷维矩阵是‘m维的2次方’特征维度谱分析（m趋于阿列夫1阶无穷大时，‘m维的2次方’仍然是阿列夫1维度特征系统），所以傅立叶谱分析下的量子态仍然表现为不确定性（阿列夫1维度傅立叶谱分析参照系，相对于阿列夫2维度特征属性的高阶张量系统不完备）。

在逻辑结构上，多层次线性关系（a的n次方维度）意味着高阶逻辑，其逻辑表达的范围（阿列夫2维特征基），远远超越了一阶逻辑的局限（阿列夫1维特征分析）。