Linear Algebra with Sub-linear Zero-Knowledge Arguments学习笔记
1. 引言
Groth 2009年论文《Linear Algebra with Sub-linear Zero-Knowledge Arguments》。
已知2个matrices A , B \mathbf{A},\mathbf{B} A,B 的commitments C A , C B C_{\mathbf{A}},C_{\mathbf{B}} CA,CB 和 1个matrix C \mathbf{C} C 的commitment C C C_{\mathbf{C}} CC,本文构建了:
- sub-linear size的零知识证明,用于证明 product of two matrices C = A ∗ B \mathbf{C}=\mathbf{A}*\mathbf{B} C=A∗B。
- sub-linear size的零知识证明,用于证明 Hadamard product of two matrices C = A ∘ B \mathbf{C}=\mathbf{A}\circ \mathbf{B} C=A∘B。
基于以上两种证明方案,可以构建其它sub-linear 零知识证明,用于证明,如:(用于证明 a set of committed vectors and matrices satisfying a set of linear algebra relations。)
- a committed matrix being upper or lower triangular;
- a committed matrix being the inverse of another committed matrix;
- a committed matrix being a permutation of another committed matrix (using either a public or a hidden permutation);
- a committed field element being the dot product of two committed vectors;
- a committed matrix being the product of two other committed matrices;
- a committed vector being the Hadamard product (the entry-wise product) of two other vectors;
- a committed matrix has a particular trace;
- compute the sums of the rows or columns of a committed matrix;
同时,可将本文技术用于证明 the satisfiability of an arithmetic circuit with N N N gates,本文所构建的arithmetic circuit 零知识证明算法具有的communication complexity 为 O ( N ) O(\sqrt{N}) O(N) 个group elements。本文提供了2种实现方式:
- 1)constant round 的零知识证明算法;
- 2) O ( log 2 N ) O(\log_2 N) O(log2N) round 的零知识证明算法,Prover的computation complexity 为 O ( N / log 2 N ) O(N/{\log_2 N}) O(N/log2N)个exponentiations,Verifier的computation complexity为 O ( N ) O(N) O(N)个multiplications。
对于只有与非门的binary circuit来说,本文基于Pedersen commitment的变体,提供了一种circuit satisfiability的public-coin 零知识证明算法:
- communication complexity为 O ( N ) O(\sqrt{N}) O(N) 个group elements;
- Prover和Verifier的computation complexity 均为 O ( N ) O(N) O(N)个multiplications。
在构建零知识证明算法时,需要同时关注communication complexity和computation complexity。本文所构建的零知识证明算法,具有sub-linear communication的同时,也具有 low computational complexity。
对于 n × n n\times n n×n矩阵 A \mathbf{A} A,以行向量表示为 A = [ a ⃗ 1 , ⋯ , a ⃗ n ] T \mathbf{A}=[\vec{a}_1,\cdots,\vec{a}_n]^T A=[a1,⋯,an]T,对每个行向量进行Pedersen commitment为 a single group element。 C o m ( A ) = [ C o m ( a ⃗ 1 ) , ⋯ , C o m ( a ⃗ n ) ] T Com(\mathbf{A})=[Com(\vec{a}_1),\cdots,Com(\vec{a}_n)]^T Com(A)=[Com(a1),⋯,Com(an)]T。
1.1 一些定义
1.2 Homomorphic Commitments
本文采用的是generalized Pedersen commitment scheme。
key generation algorithm K K K 用于生成commitment key c k = ( G , g 1 , ⋯ , g n , h ) ck=(G,g_1,\cdots,g_n,h) ck=(G,g1,⋯,gn,h),其中 g 1 , ⋯ , g n , h g_1,\cdots,g_n,h g1,⋯,gn,h 为随机选择的generators of a group G G G of prime order p p p with ∣ p ∣ = k |p|=\mathcal{k} ∣p∣=k。对应的message space 为 Z p n \mathbb{Z}_p^n Zpn,randomizer space 为 Z p \mathbb{Z}_p Zp,commitment space 为 G G G。
选择随机数 r ← Z p r\leftarrow \mathbb{Z}_p r←Zp,对vector ( x 1 , ⋯ , x n ) ∈ Z p n (x_1,\cdots,x_n)\in\mathbb{Z}_p^n (x1,⋯,xn)∈Zpn 的commitment 为:
c = c o m c k ( x ⃗ ; r ) = h r ∏ i = 1 n g i x i c=com_{ck}(\vec{x};r)=h^r\prod_{i=1}^{n}g_i^{x_i} c=comck(x;r)=hr∏i=1ngixi
以上commitment具有perfect hiding属性,同时具有computationally binding属性under the discrete logarithm assumption。
本文的SHVZK arguments中的common reference string 就是 commitment key c k ck ck。对于一些经典的group G G G,commitment key可 easily sampled from a common random string 同时可 easily verify that c k ck ck is a valid commitment key。commitment key c k ck ck 甚至可由Verifier来选择。
Pedersen commitment的具有加法同态属性:
c o m c k ( x ⃗ ; r ) ⋅ c o m c k ( x ⃗ ′ ; r ′ ) = c o m c k ( x ⃗ + x ⃗ ′ ; r + r ′ ) com_{ck}(\vec{x};r)\cdot com_{ck}(\vec{x}';r')=com_{ck}(\vec{x}+\vec{x}';r+r') comck(x;r)⋅comck(x′;r′)=comck(x+x′;r+r′)
c o m c k ( a x ⃗ + a ′ x ⃗ ′ ; a r + a ′ r ′ ) = c o m c k ( x ⃗ ; r ) a ⋅ c o m c k ( x ⃗ ′ ; r ′ ) a ′ com_{ck}(a\vec{x}+a'\vec{x}';ar+a'r')= com_{ck}(\vec{x};r)^{a}\cdot com_{ck}(\vec{x}';r')^{a'} comck(ax+a′x′;ar+a′r′)=comck(x;r)a⋅comck(x′;r′)a′
1.3 multi-exponentiation技术
采用multi-exponentiation技术,相比于单独计算 n n n 个single exponentiations,直接计算 ∏ i = 1 n g i x i \prod_{i=1}^{n}g_i^{x_i} ∏i=1ngixi会更快,这将有助于快速计算Pedersen commitment。
常用的multi-exponentiation技术主要有:
- Pippenger 1980年论文《On the evaluation of powers and monomials》中提出了一种general theory of multi-exponentiations;
- Lim 2000年论文《Efficient multi-exponentiation and application to batch verification of digital signatures》中提出了一种 concrete multi-exponentiation 技术,当 n n n 很大时,其complexity低于 2 n k / log 2 n 2n\mathcal{k}/{\log_2 n} 2nk/log2n multiplications in G G G。
本文推荐使用Lim的multi-exponentiation算法。
1.4 一些假设
2. Argument of Knowledge of Commitment Openings
基本信息为:
Public info:commitment key c k ck ck 和 a set of commitments c 1 , ⋯ , c m c_1,\cdots,c_m c1,⋯,cm。
Private info:a set of vectors x ⃗ 1 , ⋯ , x ⃗ m ∈ Z p n \vec{x}_1,\cdots,\vec{x}_m\in\mathbb{Z}_p^n x1,⋯,xm∈Zpn。
Relation:for i ∈ [ 1 , m ] i\in [1,m] i∈[1,m] 有 c i = c o m ( x ⃗ i ; r i ) c_i=com(\vec{x}_i;r_i) ci=com(xi;ri)。
Knowledge of content of commitments的证明算法为:(含3 rounds)
- 1)Prover:选择随机数 x ⃗ 0 ← Z p n , r 0 ← Z p \vec{x}_0\leftarrow\mathbb{Z}_p^n,r_0\leftarrow\mathbb{Z}_p x0←Zpn,r0←Zp,计算 c 0 = c o m c k ( x ⃗ 0 ; r 0 ) c_0=com_{ck}(\vec{x}_0;r_0) c0=comck(x0;r0),并将 c 0 c_0 c0值发送给Verifier。
- 2)Verifier:发送random challenge e ← Z p e\leftarrow \mathbb{Z}_p e←Zp。
- 3)Prover:计算 z ⃗ = ∑ i = 0 m e i x i ⃗ = ( x 01 + e x 11 + ⋯ + e m x m 1 , x 02 + e x 12 + ⋯ + e m x m 2 , ⋯ , m x 0 n + e m x 1 n + ⋯ + e m x m n ) \vec{z}=\sum_{i=0}^{m}e^i\vec{x_i}=(x_{01}+ex_{11}+\cdots+e^mx_{m1}, x_{02}+ex_{12}+\cdots+e^mx_{m2},\cdots, mx_{0n}+e^mx_{1n}+\cdots+e^mx_{mn}) z=∑i=0meixi=(x01+ex11+⋯+emxm1,x02+ex12+⋯+emxm2,⋯,mx0n+emx1n+⋯+emxmn) 和 s = ∑ i = 0 m e i r i s=\sum_{i=0}^{m}e^ir_i s=∑i=0meiri。将 z ⃗ ∈ Z p n \vec{z}\in\mathbb{Z}_p^n z∈Zpn和 s ∈ Z p s\in\mathbb{Z}_p s∈Zp发送给Verifier。
- 4)Verifier验证 ∏ i = 0 m c i e i = c o m c k ( z ⃗ ; s ) \prod_{i=0}^{m}c_i^{e^i}=com_{ck}(\vec{z};s) ∏i=0mciei=comck(z;s) 是否成立即可。
整个证明算法中,communication cost包含:1个commitment和 n + 2 n+2 n+2 个field elements。Prover计算了1个commitment、a linear combination of the vectors x ⃗ i \vec{x}_i xi 和 a linear combination of the randomizer r i r_i ri。采用multi-exponentiation 技术,Prover需要计算大约 2 n k / log 2 n 2n\mathcal{k}/{\log_2 n} 2nk/log2n 次 multiplications of group elements以及 m n mn mn 次 multiplications of field elements。Verifier采用multi-exponentiations技术来计算commitment和 multi-exponentiation of m m m commitments,需要大约 2 m k / log 2 m + 2 n k / log 2 n 2m\mathcal{k}/{\log_2 m}+2n\mathcal{k}/{\log_2 n} 2mk/log2m+2nk/log2n次multiplications in the group。整个证明算法的comminication和computation开销都比较低。
以上证明算法为3-move public coin argument with witness extended emulation for knowledge of the openings of a set of commitments,该argument具有perfect completeness和perfect SHVZK。(详细内容参见论文中Theorem 4 证明。)
3. matric、vector和element的线性代数关系表示
本文中 ∘ \circ ∘ 表示 Hadamard product (entry-wise product)。
- private info(committed info)有:矩阵 X i , Y i , Z ∈ M a t n × n ( Z p ) \mathbf{X}_i, \mathbf{Y}_i , \mathbf{Z}\in Mat_{n\times n}(\mathbb{Z}_p) Xi,Yi,Z∈Matn×n(Zp),行向量 x ⃗ i , y ⃗ i , z ⃗ ∈ Z p n \vec{x}_i,\vec{y}_i,\vec{z}\in\mathbb{Z}_p^n xi,yi,z∈Zpn 和 element z ∈ Z p z\in\mathbb{Z}_p z∈Zp。
- public info 有: a i ∈ Z p a_i\in\mathbb{Z}_p ai∈Zp。
本文主要关注6种类型的关系等式为: - (1) z ⃗ T = ∑ i = 1 m a i X i y ⃗ i T \vec{z}^T=\sum_{i=1}^{m}a_i\mathbf{X}_i\vec{y}_i^T zT=∑i=1maiXiyiT
- (2) Z = ∑ i = 1 m a i X i Y i \mathbf{Z}=\sum_{i=1}^{m}a_i\mathbf{X}_i\mathbf{Y}_i Z=∑i=1maiXiYi
- (3) Z = ∑ i = 1 m X i ∘ Y i \mathbf{Z}=\sum_{i=1}^{m}\mathbf{X}_i\circ\mathbf{Y}_i Z=∑i=1mXi∘Yi
- (4) z = ∑ i = 1 m a i x ⃗ i y ⃗ i T z=\sum_{i=1}^{m}a_i\vec{x}_i\vec{y}_i^T z=∑i=1maixiyiT
- (5) z ⃗ = ∑ i = 1 m a i x ⃗ i Y i \vec{z}=\sum_{i=1}^{m}a_i\vec{x}_i\mathbf{Y}_i z=∑i=1maixiYi
- (6) z ⃗ = ∑ i = 1 m a i x ⃗ i ∘ y ⃗ i \vec{z}=\sum_{i=1}^{m}a_i\vec{x}_i\circ\vec{y}_i z=∑i=1maixi∘yi
对于以上6种关系等式,均可转换为一系列形式如下的方程式:
z = ∑ i = 1 m x ⃗ i ∗ y ⃗ i z=\sum_{i=1}^{m}\vec{x}_i*\vec{y}_i z=∑i=1mxi∗yi
其中 ∗ : Z p n ∗ Z p n → Z p *:\mathbb{Z}_p^n*\mathbb{Z}_p^n\rightarrow \mathbb{Z}_p ∗:Zpn∗Zpn→Zp 为bilinear map。
本文中的bilinear map选择有两种:
- 用于表示标准的dot product of vectors: x ⃗ ∗ y ⃗ = x ⃗ y ⃗ T \vec{x}*\vec{y}=\vec{x}\vec{y}^T x∗y=xyT;
- 用于表示: x ⃗ ∗ y ⃗ = x ⃗ ( y ⃗ ∘ t ⃗ ) T \vec{x}*\vec{y}=\vec{x}(\vec{y}\circ\vec{t})^T x∗y=x(y∘t)T,其中 t ⃗ ∈ Z p n \vec{t}\in\mathbb{Z}_p^n t∈Zpn为由Verifier选择的public vector。
由于矩阵可以以 n n n个行向量表示,以上6种类型的前三种关系等式分别对应为 n n n个后三种关系等式。(即关系式1对应 n n n个关系式4,关系式2对应 n n n个关系式5,关系式3对应 n n n个关系式6。)
因此,将重点关注将关系式4、5、6转换为一系列形如 z = ∑ i = 1 m x ⃗ i ∗ y ⃗ i z=\sum_{i=1}^{m}\vec{x}_i*\vec{y}_i z=∑i=1mxi∗yi 的方程式。
3.1 将大量 z = ∑ i = 1 m a i x ⃗ i y ⃗ i T z=\sum_{i=1}^{m}a_i\vec{x}_i\vec{y}_i^T z=∑i=1maixiyiT reduce为一个方程式
利用Randomization,可将 Q Q Q个形如 z q = ∑ i = 1 m q a q i x ⃗ q i y ⃗ q i T z_q=\sum_{i=1}^{m_q}a_{qi}\vec{x}_{qi}\vec{y}_{qi}^T zq=∑i=1mqaqixqiyqiT的方程式reduce为一个形如 z = ∑ i = 1 m z ⃗ i y ⃗ i T , 其 中 m = ∑ q = 1 Q m q z=\sum_{i=1}^{m}\vec{z}_i\vec{y}_i^T,其中m=\sum_{q=1}^{Q}m_q z=∑i=1mziyiT,其中m=∑q=1Qmq的单一的方程式。
- Verifier选择随机数 r ← Z p r\leftarrow \mathbb{Z}_p r←Zp,构建Vandermonde matrix row 为 r ⃗ = ( r 1 , ⋯ , r Q ) = ( 1 , r , ⋯ , r Q − 1 ) \vec{r}=(r_1,\cdots,r_Q)=(1,r,\cdots,r^{Q-1}) r=(r1,⋯,rQ)=(1,r,⋯,rQ−1)。
- 1)接下来,需要Prover证明 ∑ q = 1 Q r q z q = ∑ q = 1 Q ∑ i = 1 m q ( r q a q i x ⃗ q i ) y ⃗ q i T \sum_{q=1}^{Q}r_qz_q=\sum_{q=1}^{Q}\sum_{i=1}^{m_q}(r_qa_{qi}\vec{x}_{qi})\vec{y}_{qi}^T ∑q=1Qrqzq=∑q=1Q∑i=1mq(rqaqixqi)yqiT成立。【以向量形式表示 z ⃗ = ( z 1 , ⋯ , z Q ) \vec{z}=(z_1,\cdots,z_Q) z=(z1,⋯,zQ),即相当于需证明 z ⃗ r ⃗ T = ∑ q = 1 Q ∑ i = 1 m q ( r q a q i x ⃗ q i ) y ⃗ q i T \vec{z}\vec{r}^T=\sum_{q=1}^{Q}\sum_{i=1}^{m_q}(r_qa_{qi}\vec{x}_{qi})\vec{y}_{qi}^T zrT=∑q=1Q∑i=1mq(rqaqixqi)yqiT】
该等式左右两侧均为以challenge r r r为变量的多项式,多项式的阶均为 Q − 1 Q-1 Q−1,根据Schwartz-Zippel lemma,以上等式伪造成立的概率不高于 Q − 1 p \frac{Q-1}{p} pQ−1。
可直接设置 z = ∑ q = 1 Q r q z q , x ⃗ q i ′ = r q a q i x ⃗ q i z=\sum_{q=1}^{Q}r_qz_q, \vec{x}_{qi}'= r_qa_{qi}\vec{x}_{qi} z=∑q=1Qrqzq,xqi′=rqaqixqi【因为相应的commitment可直接计算: c o m ( z ) = ∏ q = 1 Q ( c o m ( z q ) ) r q , c o m ( x ⃗ q i ′ ) = ( c o m ( x ⃗ q i ) ) r q a q i com(z)=\prod_{q=1}^{Q}(com(z_q))^{r_q}, com(\vec{x}_{qi}')=(com(\vec{x}_{qi}))^{r_qa_{qi}} com(z)=∏q=1Q(com(zq))rq,com(xqi′)=(com(xqi))rqaqi】,则有:
z = ∑ q = 1 Q ∑ i = 1 m q x ⃗ q i ′ y ⃗ q i T z=\sum_{q=1}^{Q}\sum_{i=1}^{m_q}\vec{x}_{qi}'\vec{y}_{qi}^T z=∑q=1Q∑i=1mqxqi′yqiT
3.2 将 z ⃗ = ∑ i = 1 m a i x ⃗ i Y i \vec{z}=\sum_{i=1}^{m}a_i\vec{x}_i\mathbf{Y}_i z=∑i=1maixiYi reduce为形如 z = ∑ i = 1 m a i x ⃗ i y ⃗ i T z=\sum_{i=1}^{m}a_i\vec{x}_i\vec{y}_i^T z=∑i=1maixiyiT
- Verifier:选择随机数 t ← Z p t\leftarrow \mathbb{Z}_p t←Zp,构建Vandermonde matrix row 为 t ⃗ = ( 1 , t , ⋯ , t n − 1 ) \vec{t}=(1,t,\cdots,t^{n-1}) t=(1,t,⋯,tn−1)。
- 1)接下来,需要Prover证明 z ⃗ t ⃗ T = ( ∑ i = 1 m a i x ⃗ i Y i ) t ⃗ T = ∑ i = 1 m a i x ⃗ i ( Y i t ⃗ T ) \vec{z}\vec{t}^T=(\sum_{i=1}^{m}a_{i}\vec{x}_{i}\mathbf{Y}_i)\vec{t}^T=\sum_{i=1}^{m}a_{i}\vec{x}_{i}(\mathbf{Y}_i\vec{t}^T) ztT=(∑i=1maixiYi)tT=∑i=1maixi(YitT)成立。
该等式左右两侧均为以challenge t t t为变量的多项式,多项式的阶均为 n − 1 n-1 n−1,根据Schwartz-Zippel lemma,以上等式伪造成立的概率不高于 n − 1 p \frac{n-1}{p} pn−1。
存在的问题是:已知矩阵 Y i \mathbf{Y}_i Yi的每行向量的commitment,无法直接计算 Y i t ⃗ T \mathbf{Y}_i\vec{t}^T YitT的commitment。为证明the linear combination of the columns,需要额外再引入2个round:【矩阵转置运算有 ( A B ) T = B T A T (\mathbf{A}\mathbf{B})^T=\mathbf{B}^T\mathbf{A}^T (AB)T=BTAT,因此有 ( Y i t ⃗ T ) T = t ⃗ Y i T (\mathbf{Y}_i\vec{t}^T)^T=\vec{t}\mathbf{Y}_i^T (YitT)T=tYiT】 - 2)Prover 针对向量 y ⃗ i = t ⃗ Y i T \vec{y}_i=\vec{t}\mathbf{Y}_i^T yi=tYiT 计算commitment C y ⃗ i = c o m ( y ⃗ i ) C_{\vec{y}_i}=com(\vec{y}_i) Cyi=com(yi),并将 C y ⃗ i C_{\vec{y}_i} Cyi 发送给Verifier。
由步骤1)中的等式证明改为证明 z ⃗ t ⃗ T − ∑ i = 1 m a i x ⃗ i y ⃗ i T = 0 \vec{z}\vec{t}^T-\sum_{i=1}^{m}a_{i}\vec{x}_{i}\vec{y}_i^T=0 ztT−∑i=1maixiyiT=0成立且证明 y ⃗ i = t ⃗ Y i T \vec{y}_i=\vec{t}\mathbf{Y}_i^T yi=tYiT。 - Verifier:选择随机数 s ← Z p s\leftarrow \mathbb{Z}_p s←Zp,构建Vandermonde matrix row 为 s ⃗ = ( 1 , s , ⋯ , s n − 1 ) \vec{s}=(1,s,\cdots,s^{n-1}) s=(1,s,⋯,sn−1)。【对于向量的dot product表示,有 a ⃗ b ⃗ T = b ⃗ a ⃗ T \vec{a}\vec{b}^T=\vec{b}\vec{a}^T abT=baT,于是有 y i ⃗ s ⃗ T = s ⃗ y ⃗ i T = s ⃗ Y i t ⃗ T = ( s ⃗ Y i ) t ⃗ T \vec{y_i}\vec{s}^T=\vec{s}\vec{y}_i^T=\vec{s}\mathbf{Y}_i\vec{t}^T=(\vec{s}\mathbf{Y}_i)\vec{t}^T yisT=syiT=sYitT=(sYi)tT】
- Prover:
– (a) 对于 y ⃗ i = t ⃗ Y i T \vec{y}_i=\vec{t}\mathbf{Y}_i^T yi=tYiT 改为证明 y i ⃗ s ⃗ T = ( s ⃗ Y i ) t ⃗ T \vec{y_i}\vec{s}^T=(\vec{s}\mathbf{Y}_i)\vec{t}^T yisT=(sYi)tT 成立。
注意此时, ( s ⃗ Y i ) (\vec{s}\mathbf{Y}_i) (sYi)为矩阵 Y i \mathbf{Y}_i Yi行向量的线性组合,所以相应的commitment可直接基于矩阵 Y i \mathbf{Y}_i Yi行向量 Y i ⃗ j \vec{Y_i}_j Yij的commitment计算—— c o m ( s ⃗ Y i ) = ∏ j = 1 n ( c o m ( Y i ⃗ j ) ) s j com(\vec{s}\mathbf{Y}_i)=\prod_{j=1}^{n}(com(\vec{Y_i}_j))^{s_j} com(sYi)=∏j=1n(com(Yij))sj。此处可实现 y ⃗ i = t ⃗ Y i T \vec{y}_i=\vec{t}\mathbf{Y}_i^T yi=tYiT证明。【??相当于3.1节中, Q = 1 , m = 1 Q=1,m=1 Q=1,m=1 的特例情况,可转换为3.1节中的证明。】
– (b) 对于 z ⃗ t ⃗ T − ∑ i = 1 m a i x ⃗ i y ⃗ i T = 0 \vec{z}\vec{t}^T-\sum_{i=1}^{m}a_{i}\vec{x}_{i}\vec{y}_i^T=0 ztT−∑i=1maixiyiT=0的证明,相当于3.1中 Q = 1 Q=1 Q=1 的特例情况,可转换为3.1节中的证明。
【??注意此处不再是对整个 z ⃗ \vec{z} z向量的commitment,而应该是对其中每个元素进行commitment,这样才能计算 c o m ( z ⃗ t ⃗ T ) = ∏ i = 1 n ( c o m ( z i ) ) t i com(\vec{z}\vec{t}^T)=\prod_{i=1}^{n}(com(z_i))^{t_i} com(ztT)=∏i=1n(com(zi))ti】
以上整个reduction中的主要开销在于:
- 计算 y ⃗ i \vec{y}_i yi;
- 计算 s ⃗ Y i \vec{s}\mathbf{Y}_i sYi;
- 计算 y ⃗ i \vec{y}_i yi的commitments。
3.3 将大量 z ⃗ = ∑ i = 1 m a i x ⃗ i ∘ y ⃗ i \vec{z}=\sum_{i=1}^{m}a_i\vec{x}_i\circ\vec{y}_i z=∑i=1maixi∘yi Hadamard Products reduce为a single Equation with a Bilinear Map
利用Randomization,可将 Q Q Q个形如 z ⃗ q = ∑ i = 1 m q a q i x ⃗ q i ∘ y ⃗ q i \vec{z}_q=\sum_{i=1}^{m_q}a_{qi}\vec{x}_{qi}\circ\vec{y}_{qi} zq=∑i=1mqaqixqi∘yqi的方程式reduce为一个单一的具有Bilinear Map的方程式。
- Verifier选择随机数 r ← Z p r\leftarrow \mathbb{Z}_p r←Zp,构建Vandermonde matrix row 为 r ⃗ = ( r 1 , ⋯ , r Q ) = ( 1 , r , ⋯ , r Q − 1 ) \vec{r}=(r_1,\cdots,r_Q)=(1,r,\cdots,r^{Q-1}) r=(r1,⋯,rQ)=(1,r,⋯,rQ−1)。
- 1)接下来,需要Prover证明 ∑ q = 1 Q r q z ⃗ q = ∑ q = 1 Q ∑ i = 1 m q ( r q a q i x ⃗ q i ) ∘ y ⃗ q i \sum_{q=1}^{Q}r_q\vec{z}_q=\sum_{q=1}^{Q}\sum_{i=1}^{m_q}(r_qa_{qi}\vec{x}_{qi})\circ\vec{y}_{qi} ∑q=1Qrqzq=∑q=1Q∑i=1mq(rqaqixqi)∘yqi成立。
该等式左右两侧均为以challenge r r r为变量的多项式,多项式的阶均为 Q − 1 Q-1 Q−1,根据Schwartz-Zippel lemma,以上等式伪造成立的概率不高于 Q − 1 p \frac{Q-1}{p} pQ−1。
可直接设置 z ⃗ ′ = ∑ q = 1 Q r q z ⃗ q , x ⃗ q i ′ = r q a q i x ⃗ q i \vec{z}'=\sum_{q=1}^{Q}r_q\vec{z}_q, \vec{x}_{qi}'= r_qa_{qi}\vec{x}_{qi} z′=∑q=1Qrqzq,xqi′=rqaqixqi【因为相应的commitment可直接计算: c o m ( z ⃗ ′ ) = ∏ q = 1 Q ( c o m ( z ⃗ q ) ) r q , c o m ( x ⃗ q i ′ ) = ( c o m ( x ⃗ q i ) ) r q a q i com(\vec{z}')=\prod_{q=1}^{Q}(com(\vec{z}_q))^{r_q}, com(\vec{x}_{qi}')=(com(\vec{x}_{qi}))^{r_qa_{qi}} com(z′)=∏q=1Q(com(zq))rq,com(xqi′)=(com(xqi))rqaqi】,则有a Hadamard equation:
z ⃗ ′ = ∑ q = 1 Q ∑ i = 1 m q x ⃗ q i ′ ∘ y ⃗ q i T \vec{z}'=\sum_{q=1}^{Q}\sum_{i=1}^{m_q}\vec{x}_{qi}'\circ\vec{y}_{qi}^T z′=∑q=1Q∑i=1mqxqi′∘yqiT
对于形如 z ⃗ = ∑ i = 1 m x ⃗ i ∘ y ⃗ i \vec{z}=\sum_{i=1}^{m}\vec{x}_i\circ\vec{y}_i z=∑i=1mxi∘yi的Hadamard 方程式的证明:
- Verifier选择随机数 t ← Z p t\leftarrow \mathbb{Z}_p t←Zp,构建Vandermonde matrix row 为 t ⃗ = ( t 1 , ⋯ , t Q ) = ( 1 , t , ⋯ , t Q − 1 ) \vec{t}=(t_1,\cdots,t_Q)=(1,t,\cdots,t^{Q-1}) t=(t1,⋯,tQ)=(1,t,⋯,tQ−1)。
- 2)接下来,需要Prover 证明 z ⃗ t ⃗ T = ( ∑ i = 1 m x ⃗ i ∘ y ⃗ i ) t ⃗ T = ∑ i = 1 m x ⃗ i ( y ⃗ i ∘ t ⃗ ) T \vec{z}\vec{t}^T=(\sum_{i=1}^{m}\vec{x}_i\circ\vec{y}_i)\vec{t}^T=\sum_{i=1}^{m}\vec{x}_i(\vec{y}_i\circ\vec{t})^T ztT=(∑i=1mxi∘yi)tT=∑i=1mxi(yi∘t)T
定义bilinear map为:
∗ : Z p n × Z p n → Z p ( x ⃗ , y ⃗ ) → x ⃗ ( y ⃗ ∘ t ⃗ ) T *:\mathbb{Z}_p^n\times\mathbb{Z}_p^n\rightarrow \mathbb{Z}_p\ \ \ \ \ \ (\vec{x},\vec{y})\rightarrow \vec{x}(\vec{y}\circ\vec{t})^T ∗:Zpn×Zpn→Zp (x,y)→x(y∘t)T
于是转为证明 0 = ∑ i = 1 m x ⃗ i ∗ y ⃗ i − z ⃗ ∗ 1 ⃗ 0=\sum_{i=1}^{m}\vec{x}_i*\vec{y}_i-\vec{z}*\vec{1} 0=∑i=1mxi∗yi−z∗1,其中 1 ⃗ = ( 1 , 1 , ⋯ , 1 ) \vec{1}=(1,1,\cdots,1) 1=(1,1,⋯,1)。
4. Vector Product Equation的零知识证明
第3节中提到的6种方程式,均可以转换为形如 z = ∑ i = 1 m x ⃗ i ∗ y ⃗ i z=\sum_{i=1}^{m}\vec{x}_i*\vec{y}_i z=∑i=1mxi∗yi的方程式,其中 ∗ * ∗代表2种bilinear map:
- 用于表示标准的dot product of vectors: x ⃗ ∗ y ⃗ = x ⃗ y ⃗ T \vec{x}*\vec{y}=\vec{x}\vec{y}^T x∗y=xyT;
- 用于表示: x ⃗ ∗ y ⃗ = x ⃗ ( y ⃗ ∘ t ⃗ ) T \vec{x}*\vec{y}=\vec{x}(\vec{y}\circ\vec{t})^T x∗y=x(y∘t)T,其中 t ⃗ = ( 1 , t , ⋯ , t n − 1 ) ∈ Z p n \vec{t}=(1,t,\cdots,t^{n-1})\in\mathbb{Z}_p^n t=(1,t,⋯,tn−1)∈Zpn为由Verifier选择的public vector。
基本信息:
- public info:commitment key c k ck ck及其他commitments。
- private info: z ∈ Z p , x ⃗ 1 , y ⃗ 1 , ⋯ , ⋯ , x ⃗ m , y ⃗ m ∈ Z p n z\in\mathbb{Z}_p,\vec{x}_1,\vec{y}_1,\cdots,\cdots,\vec{x}_m,\vec{y}_m\in\mathbb{Z}_p^n z∈Zp,x1,y1,⋯,⋯,xm,ym∈Zpn。
- relation: z = ∑ i = 1 m x ⃗ i ∗ y ⃗ i z=\sum_{i=1}^{m}\vec{x}_i*\vec{y}_i z=∑i=1mxi∗yi。
接下来,将针对以上场景构建的零知识证明算法。
4.1 m = 1 m=1 m=1的最小化情况
首先,考虑 m = 1 m=1 m=1的最小化情况下,基本信息为:
- public info:commitment key c k ck ck 及 commitments a = c o m c k ( x ⃗ ; r ) , b = c o m c k ( y ⃗ ; s ) , c = c o m c k ( z ; t ) a=com_{ck}(\vec{x};r),b=com_{ck}(\vec{y};s),c=com_{ck}(z;t) a=comck(x;r),b=comck(y;s),c=comck(z;t)。
- private info: r , s , t , z ∈ Z p , x ⃗ , y ⃗ ∈ Z p n r,s,t,z\in\mathbb{Z}_p,\vec{x},\vec{y}\in\mathbb{Z}_p^n r,s,t,z∈Zp,x,y∈Zpn。
- relation: z = x ⃗ ∗ y ⃗ z=\vec{x}*\vec{y} z=x∗y。
【证明算法主要构建基础为: ( e x ⃗ + d ⃗ x ) ∗ ( e y ⃗ + d ⃗ y ) = e 2 x ⃗ ∗ y ⃗ + e ( x ⃗ ∗ d ⃗ x + y ⃗ ∗ d ⃗ y ) + d ⃗ x ∗ d ⃗ y (e\vec{x}+\vec{d}_x)*(e\vec{y}+\vec{d}_y)=e^2\vec{x}*\vec{y}+e(\vec{x}*\vec{d}_x+\vec{y}*\vec{d}_y)+\vec{d}_x*\vec{d}_y (ex+dx)∗(ey+dy)=e2x∗y+e(x∗dx+y∗dy)+dx∗dy。】
针对 m = 1 m=1 m=1的最小化情况的证明为:
-
Prover:选择随机数 d ⃗ x , d ⃗ y ← Z p n , d z ← Z p , r d , s d , t 1 , t 0 ← Z p \vec{d}_x,\vec{d}_y\leftarrow\mathbb{Z}_p^n,d_z\leftarrow\mathbb{Z}_p,r_d,s_d,t_1,t_0\leftarrow\mathbb{Z}_p dx,dy←Zpn,dz←Zp,rd,sd,t1,t0←Zp,计算如下commitments:
a d = c o m c k ( d ⃗ x ; r d ) , b d = c o m c k ( d ⃗ y ; s d ) , c 1 = c o m c k ( x ⃗ ∗ d ⃗ x + y ⃗ ∗ d ⃗ y ; t 1 ) , c 0 = c o m c k ( d ⃗ x ∗ d ⃗ y ; t 0 ) a_d=com_{ck}(\vec{d}_x;r_d),b_d=com_ck(\vec{d}_y;s_d),c_1=com_{ck}(\vec{x}*\vec{d}_x+\vec{y}*\vec{d}_y;t_1),c_0=com_{ck}(\vec{d}_x*\vec{d}_y;t_0) ad=comck(dx;rd),bd=comck(dy;sd),c1=comck(x∗dx+y∗dy;t1),c0=comck(dx∗dy;t0)
将commitments a d , b d , c 1 , c 0 a_d,b_d,c_1,c_0 ad,bd,c1,c0 发送给Verifier。 -
Verifier:选择随机challenge e ← Z p e\leftarrow \mathbb{Z}_p e←Zp发送给Prover。
-
Prover:计算:
f ⃗ x = e x ⃗ + d ⃗ x , f ⃗ y = e y ⃗ + d ⃗ y , r x = e r + r d , s y = e s + s d , t z = e 2 t + e t 1 + t 0 \vec{f}_x=e\vec{x}+\vec{d}_x,\vec{f}_y=e\vec{y}+\vec{d}_y,r_x=er+r_d,s_y=es+s_d,t_z=e^2t+et_1+t_0 fx=ex+dx,fy=ey+dy,rx=er+rd,sy=es+sd,tz=e2t+et1+t0
将 f ⃗ x , f ⃗ y , r x , s y , t z \vec{f}_x,\vec{f}_y,r_x,s_y,t_z fx,fy,rx,sy,tz发送给Verifier。 -
Verifier:验证以下方程式是否均成立:
a e a d = c o m c k ( f ⃗ x ; r x ) ∧ b e b d = c o m c k ( f ⃗ y ; s y ) ∧ c e 2 c 1 e c 0 = c o m c k ( f ⃗ x ∗ f ⃗ y ; t z ) a^ea_d=com_{ck}(\vec{f}_x;r_x)\wedge b^eb_d=com_{ck}(\vec{f}_y;s_y)\wedge c^{e^2}c_1^ec_0=com_{ck}(\vec{f}_x*\vec{f}_y;t_z) aead=comck(fx;rx)∧bebd=comck(fy;sy)∧ce2c1ec0=comck(fx∗fy;tz)。
以上算法的:
- communication cost为:4个commitment和 2 n + 3 2n+3 2n+3 个field elements,对于large n n n来说,对应大约 2 n k 2n\mathcal{k} 2nk bits。
- Prover的computation cost 为:计算commitments a d , b d a_d,b_d ad,bd。可采用Lim的multi-exponentiation技术,对应为 4 n k / log 2 n 4n\mathcal{k}/{\log_2 n} 4nk/log2n个multiplications in G G G。
- Veriifer的computation cost为:计算 f ⃗ x , f ⃗ y \vec{f}_x,\vec{f}_y fx,fy的commitments,可采用Lim的multi-exponentiation技术,对应也为 4 n k / log 2 n 4n\mathcal{k}/{\log_2 n} 4nk/log2n个multiplications in G G G。但是,可在此基础上再采用randomization技术,再次reduce为 2 n k / log 2 n 2n\mathcal{k}/{\log_2 n} 2nk/log2n个multiplications in G G G,具体实现方法为:Verifier引入随机数 α ← Z p \alpha\leftarrow\mathbb{Z}_p α←Zp,同时验证2个commitments的方程式 ( a e a d ) α b e b d = c o m c k ( α f ⃗ x + f ⃗ y ; α r x + s y ) (a^ea_d)^{\alpha}b^eb_d=com_{ck}(\alpha\vec{f}_x+\vec{f}_y;\alpha r_x+s_y) (aead)αbebd=comck(αfx+fy;αrx+sy)。
4.2 将 m > 1 m> 1 m>1的情况通过2-round reduce为 m = 1 m=1 m=1的最小化情况
m > 1 m> 1 m>1时,基本信息为:
- public info:commitment key c k ck ck 及 commitments a 1 = c o m c k ( x ⃗ 1 ; r 1 ) , b 1 = c o m c k ( y ⃗ 1 ; s 1 ) , ⋯ , ⋯ , a m = c o m c k ( x ⃗ m ; r m ) , b m = c o m c k ( y ⃗ m ; s m ) , c = c o m c k ( z ; t ) a_1=com_{ck}(\vec{x}_1;r_1),b_1=com_{ck}(\vec{y}_1;s_1),\cdots,\cdots,a_m=com_{ck}(\vec{x}_m;r_m),b_m=com_{ck}(\vec{y}_m;s_m),c=com_{ck}(z;t) a1=comck(x1;r1),b1=comck(y1;s1),⋯,⋯,am=comck(xm;rm),bm=comck(ym;sm),c=comck(z;t)。
- private info: r 1 , s 1 , ⋯ , ⋯ , r m , s m , t , z ∈ Z p , x ⃗ 1 , y ⃗ 1 , ⋯ , ⋯ , x ⃗ m , y ⃗ m ∈ Z p n r_1,s_1,\cdots,\cdots,r_m,s_m,t,z\in\mathbb{Z}_p,\vec{x}_1,\vec{y}_1,\cdots,\cdots,\vec{x}_m,\vec{y}_m\in\mathbb{Z}_p^n r1,s1,⋯,⋯,rm,sm,t,z∈Zp,x1,y1,⋯,⋯,xm,ym∈Zpn。
- relation: z = ∑ i = 1 m x ⃗ ∗ y ⃗ z=\sum_{i=1}^{m}\vec{x}*\vec{y} z=∑i=1mx∗y。
证明思路为:
1)将以上 m > 1 m> 1 m>1的情况通过2-round reduce为 m = 1 m=1 m=1的最小化情况;
2)reduce为 m = 1 m=1 m=1后,直接调用4.1节证明算法进行证明。
将以上 m > 1 m> 1 m>1的情况通过2-round reduce为 m = 1 m=1 m=1的最小化情况, z = ∑ i = 1 m x ⃗ ∗ y ⃗ z=\sum_{i=1}^{m}\vec{x}*\vec{y} z=∑i=1mx∗y主要构建思路为展开为如下矩阵表示,同时取所有对角线元素之和:(共有 2 m − 1 2m-1 2m−1条对角线,其中 c m − 1 = c o m c k ( z ; t ) = c c_{m-1}=com_{ck}(z;t)=c cm−1=comck(z;t)=c)

详细的实现过程为:
-
Prover:for 0 ≤ l ≤ 2 m − 2 0\leq l\leq 2m-2 0≤l≤2m−2,选择随机数 t l ← Z p t_l\leftarrow \mathbb{Z}_p tl←Zp,为保证主对角线 c m − 1 = c o m c k ( z ; t ) = c c_{m-1}=com_{ck}(z;t)=c cm−1=comck(z;t)=c,需设置 t m − 1 = t t_{m-1}=t tm−1=t。Prover计算除主对角线之外的其它对角线元素之和的commitment,对应为 for 0 ≤ l ≤ 2 m − 2 , l ≠ m − 1 0\leq l\leq 2m-2,l\neq m-1 0≤l≤2m−2,l=m−1, c l = c o m c k ( ∑ i , j ; l = m + i − j − 1 x ⃗ i ∗ y ⃗ j ; t l ) c_l=com_{ck}(\sum_{i,j;l=m+i-j-1}\vec{x}_i*\vec{y}_j;t_l) cl=comck(∑i,j;l=m+i−j−1xi∗yj;tl)。将commitments c 0 , ⋯ , c 2 m − 2 c_0,\cdots,c_{2m-2} c0,⋯,c2m−2 发送给Verifier。
-
Verifier: 发送random challenge e ← Z p e\leftarrow \mathbb{Z}_p e←Zp。
-
Prover:定义commitments a ′ = c o m c k ( x ⃗ ′ ; r ′ ) = ∏ i = 1 m a i e i − 1 , b ′ = c o m c k ( y ⃗ ′ ; s ′ ) = ∏ j = 1 m b j e m − j , c ′ = c o m c k ( z ′ ; t ′ ) = ∏ l = 0 2 m − 2 c l e l a'=com_{ck}(\vec{x}';r')=\prod_{i=1}^{m}a_i^{e^{i-1}},b'=com_{ck}(\vec{y}';s')=\prod_{j=1}^{m}b_j^{e^{m-j}},c'=com_{ck}(z';t')=\prod_{l=0}^{2m-2}c_l^{e^l} a′=comck(x′;r′)=∏i=1maiei−1,b′=comck(y′;s′)=∏j=1mbjem−j,c′=comck(z′;t′)=∏l=02m−2clel
Prover计算与这些commitments对应的openings:
x ⃗ ′ = ∑ i = 1 m e i − 1 x ⃗ i , r ′ = ∑ i = 1 m e i − 1 r i , y ⃗ ′ = ∑ j = 1 m e m − j y ⃗ j , s ′ = ∑ j = 1 m e m − j s j \vec{x}'=\sum_{i=1}^{m}e^{i-1}\vec{x}_i,r'=\sum_{i=1}^{m}e^{i-1}r_i,\vec{y}'=\sum_{j=1}^{m}e^{m-j}\vec{y}_j,s'=\sum_{j=1}^{m}e^{m-j}s_j x′=∑i=1mei−1xi,r′=∑i=1mei−1ri,y′=∑j=1mem−jyj,s′=∑j=1mem−jsj
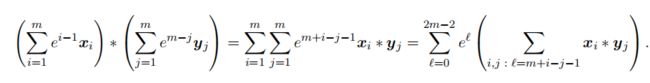
从而改为证明 z ′ = x ⃗ ′ ∗ y ⃗ ′ = ∑ l = 0 2 m − 2 e l ∑ i , j : l = m + i − j − 1 x ⃗ i ∗ y ⃗ j z'=\vec{x}' * \vec{y}'=\sum_{l=0}^{2m-2}e^l\sum_{i,j:l=m+i-j-1}\vec{x}_i*\vec{y}_j z′=x′∗y′=∑l=02m−2el∑i,j:l=m+i−j−1xi∗yj,而 t ′ = ∑ l = 0 2 m − 2 e l t l t'=\sum_{l=0}^{2m-2}e^lt_l t′=∑l=02m−2eltl。
基本信息为:
– public info:commitments a ′ = c o m c k ( x ⃗ ′ ; r ′ ) , b ′ = c o m c k ( y ⃗ ′ ; s ′ ) , c ′ = c o m c k ( z ′ ; t ′ ) a'=com_{ck}(\vec{x}';r'),b'=com_{ck}(\vec{y}';s'),c'=com_{ck}(z';t') a′=comck(x