莫烦---Pytorch学习
今天翻翻资料,发现有些地方的说明不太到位,修改过来了。
Will Yip
2020.7.29
莫烦大神Pytorch -->> 学习视频地址
2020年开年就遇上疫情,还不能上学,有够难受的,正好静一静,整理一下之前的笔记。
2020.02.26
Numpy与Torch之间的转换
import torch
import numpy as np
np_data = np.arange(6).reshape((2,3))
torch_data = torch.from_numpy(np_data)
tensor2array = torch_data.numpy()
print('\nnumpy',np_data,
'\ntorch',torch_data,
'\ntensor2array',tensor2array)
Output:
numpy [[0 1 2]
[3 4 5]]
torch tensor([[0, 1, 2],
[3, 4, 5]])
tensor2array [[0 1 2]
[3 4 5]]
跟其他搭网络的工具一样,所有的API都在官方提供的手册里可以找到:
API手册
所有在pytorch里的计算,都要先转换为tensor的形式,不然就报错,切记。
Torch中的数学运算
Abs 绝对值
# abs 绝对值计算
data = [-1, -2, 1, 2]
tensor = torch.FloatTensor(data) # 转换成32位浮点 tensor
print(
'\nabs',
'\nnumpy: ', np.abs(data),
'\ntorch: ', torch.abs(tensor)
)
Output:
abs
numpy: [1 2 1 2]
torch: tensor([1., 2., 1., 2.])
Sin 三角函数
# sin 三角函数 sin
print(
'\nsin',
'\nnumpy: ', np.sin(data),
'\ntorch: ', torch.sin(tensor)
)
Output:
sin
numpy: [-0.84147098 -0.90929743 0.84147098 0.90929743]
torch: tensor([-0.8415, -0.9093, 0.8415, 0.9093])
Mean 均值
# mean 均值
print(
'\nmean',
'\nnumpy: ', np.mean(data),
'\ntorch: ', torch.mean(tensor)
)
Output:
mean
numpy: 0.0
torch: tensor(0.)
矩阵运算
注意,有些numpy的封装的函数跟pytorch的不一样,这一点一定要区分清楚,也是很容易出问题的一个地方。
# matrix multiplication 矩阵点乘
data = [[1,2], [3,4]]
tensor = torch.FloatTensor(data) # 转换成32位浮点 tensor
# correct method
print(
'\nmatrix multiplication (matmul)',
'\nnumpy: ', data.dot(data), # [[7, 10], [15, 22]] 在numpy 中可行
'\ntorch: ', tensor.dot(tensor) # torch 会转换成 [1,2,3,4].dot([1,2,3,4) = 30.0
)
RuntimeError: dot: Expected 1-D argument self, but got 2-D
如果这样使用tensor.dot(tensor)会报错,莫烦的教程里面会输出结果为30,这应该是之后版本又更新了的缘故。只要知道这个点就好了。
注意:numpy中dot函数跟pytorch的区别
定义Variable
import torch
from torch.autograd import Variable # torch 中 Variable 模块
# 先生鸡蛋
tensor = torch.FloatTensor([[1,2],[3,4]])
# 把鸡蛋放到篮子里, requires_grad是参不参与误差反向传播, 要不要计算梯度
variable = Variable(tensor, requires_grad=True)
print(tensor)
"""
1 2
3 4
[torch.FloatTensor of size 2x2]
"""
print(variable)
"""
Variable containing:
1 2
3 4
[torch.FloatTensor of size 2x2]
"""
Output:
tensor([[1., 2.],
[3., 4.]])
tensor([[1., 2.],
[3., 4.]], requires_grad=True)
'\nVariable containing:\n 1 2\n 3 4\n[torch.FloatTensor of size 2x2]\n'
Variable 计算,梯度
比较tensor的计算和variable的计算,在正向传播它们是看不出有什么不同的,只有在反向传播才能发现它们之间的不同。
t_out = torch.mean(tensor*tensor) # x^2
v_out = torch.mean(variable*variable) # x^2
print(t_out)
print(v_out) # 7.5
Output:
tensor(7.5000)
tensor(7.5000, grad_fn=)
而且variable和tensor有个很大的区别,variable是存储变量的,是会改变的,而tensor是不会改变的,是我们输入时就设定好的参数,variable会在反向传播后修正自己的数值。 这是我觉得他们最大的不同。
v_out = torch.mean(variable*variable)就是给各个variable搭建一个运算的步骤,搭建的网络也是其中一种运算的步骤。至于怎么安排这些步骤,就看自己需要什么要的神经网络。
v_out.backward() # 模拟 v_out 的误差反向传递
# 下面两步看不懂没关系, 只要知道 Variable 是计算图的一部分, 可以用来传递误差就好.
# v_out = 1/4 * sum(variable*variable) 这是计算图中的 v_out 计算步骤
# 针对于 v_out 的梯度就是, d(v_out)/d(variable) = 1/4*2*variable = variable/2
print(variable.grad) # 初始 Variable 的梯度
'''
0.5000 1.0000
1.5000 2.0000
'''
获取Variable里面的数据
直接print(variable)只会输出 Variable形式的数据, 在很多时候是用不了的(比如想要用 plt 画图), 需要转换成tensor形式.
print(variable) # Variable 形式
"""
Variable containing:
1 2
3 4
[torch.FloatTensor of size 2x2]
"""
print(variable.data) # tensor 形式
"""
1 2
3 4
[torch.FloatTensor of size 2x2]
"""
print(variable.data.numpy()) # numpy 形式
"""
[[ 1. 2.]
[ 3. 4.]]
"""
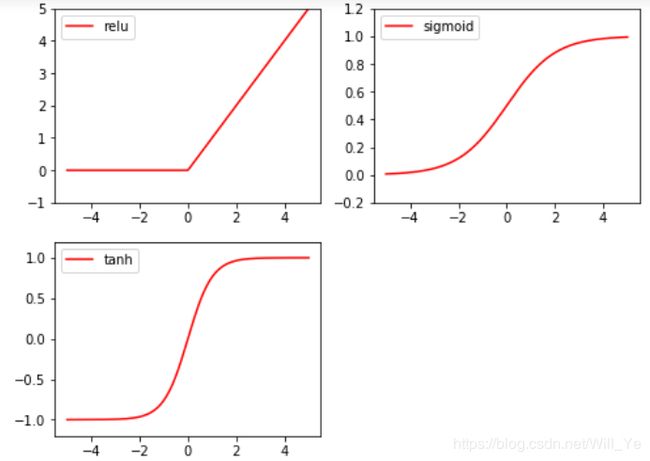
常用几种激励函数及图像
常用几种激励函数:relu, sigmoid, tanh, softplus
import torch
import torch.nn.functional as F # 激励函数都在这
from torch.autograd import Variable
# 做一些假数据来观看图像
x = torch.linspace(-5, 5, 200) # x data (tensor), shape=(100, 1)
x = Variable(x)
莫烦大神那时的版本用的是torch.nn.relu,但后来版本改了,直接用torch.relu就可以,其他激励函数也一样。
x_np = x.data.numpy() # 换成 numpy array, 出图时用
# 几种常用的 激励函数
y_relu = torch.relu(x).data.numpy()
y_sigmoid = torch.sigmoid(x).data.numpy()
y_tanh = torch.tanh(x).data.numpy()
#y_softplus = torch.softplus(x).data.numpy()
# y_softmax = F.softmax(x) softmax 比较特殊, 不能直接显示, 不过他是关于概率的, 用于分类
然后再用matplotlib库的函数就可以输出图像了,后来我发现还有其他库的制图也很不错。
import matplotlib.pyplot as plt # python 的可视化模块, 我有教程 (https://morvanzhou.github.io/tutorials/data-manipulation/plt/)
plt.figure(1, figsize=(8, 6))
plt.subplot(221)
plt.plot(x_np, y_relu, c='red', label='relu')
plt.ylim((-1, 5))
plt.legend(loc='best')
plt.subplot(222)
plt.plot(x_np, y_sigmoid, c='red', label='sigmoid')
plt.ylim((-0.2, 1.2))
plt.legend(loc='best')
plt.subplot(223)
plt.plot(x_np, y_tanh, c='red', label='tanh')
plt.ylim((-1.2, 1.2))
plt.legend(loc='best')
'''
plt.subplot(224)
plt.plot(x_np, y_softplus, c='red', label='softplus')
plt.ylim((-0.2, 6))
plt.legend(loc='best')
'''
plt.show()
拟合回归
1.建立数据集
import torch
import matplotlib.pyplot as plt
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size()) # noisy y data (tensor), shape=(100, 1)
# 画图
plt.scatter(x.data.numpy(), y.data.numpy())
plt.show()
2.建立一个只有一个隐藏层的神经网络
先定义所有的层属性(init()), 然后再一层层搭建(forward(x))层于层的关系链接
import torch
import torch.nn.functional as F # 激励函数都在这
class Net(torch.nn.Module): # 继承 torch 的 Module
def __init__(self, n_feature, n_hidden, n_output):
super(Net, self).__init__() # 继承 __init__ 功能
# 定义每层用什么样的形式
self.hidden = torch.nn.Linear(n_feature, n_hidden) # 隐藏层线性输出
self.predict = torch.nn.Linear(n_hidden, n_output) # 输出层线性输出
def forward(self, x): # 这同时也是 Module 中的 forward 功能
# 正向传播输入值, 神经网络分析出输出值
x = F.relu(self.hidden(x)) # 激励函数(隐藏层的线性值)
x = self.predict(x) # 输出值
return x
net = Net(n_feature=1, n_hidden=10, n_output=1)
print(net) # net 的结构
"""
Net (
(hidden): Linear (1 -> 10)
(predict): Linear (10 -> 1)
)
"""
Output:
Net(
(hidden): Linear(in_features=1, out_features=10, bias=True)
(predict): Linear(in_features=10, out_features=1, bias=True)
)
'\nNet (\n (hidden): Linear (1 -> 10)\n (predict): Linear (10 -> 1)\n)\n'
3.训练网络
# optimizer 是训练的工具
optimizer = torch.optim.SGD(net.parameters(), lr=0.2) # 传入 net 的所有参数, 学习率
loss_func = torch.nn.MSELoss() # 预测值和真实值的误差计算公式 (均方差)
for t in range(100):
prediction = net(x) # 喂给 net 训练数据 x, 输出预测值
loss = loss_func(prediction, y) # 计算两者的误差
optimizer.zero_grad() # 清空上一步的残余更新参数值
loss.backward() # 误差反向传播, 计算参数更新值
optimizer.step() # 将参数更新值施加到 net 的 parameters 上
注意loss_func(prediction, y)中两个参数的位置,不要调换,有时会产生不同结果的情况出现。
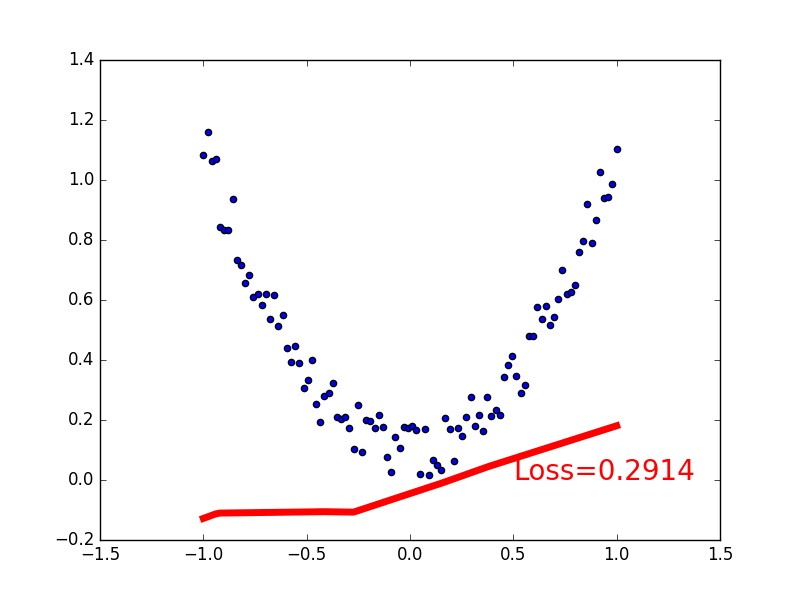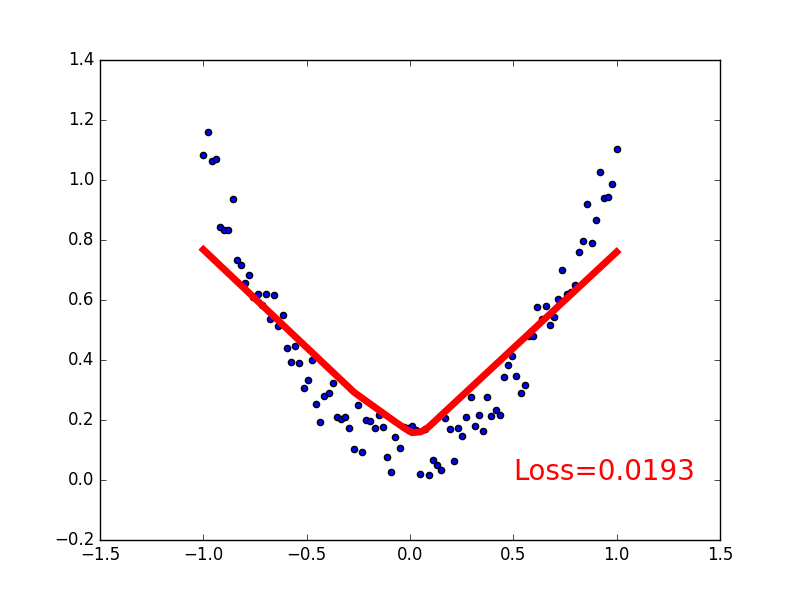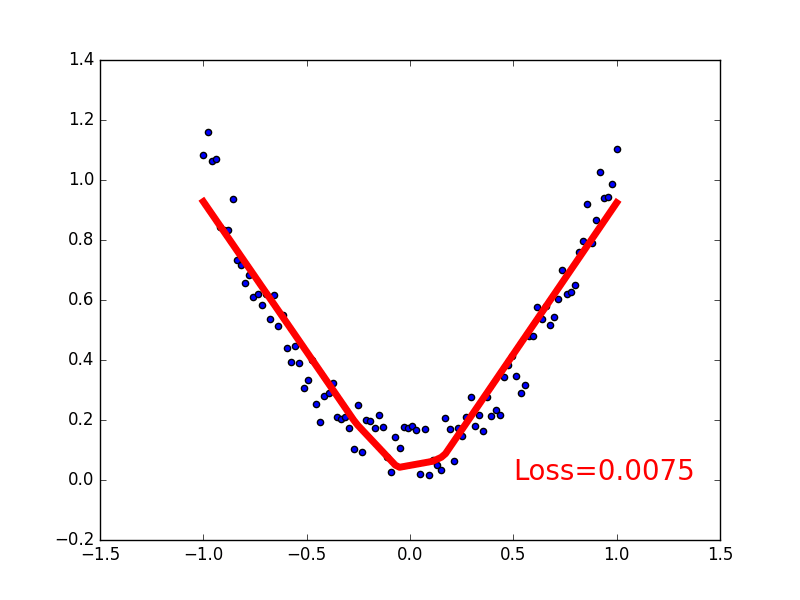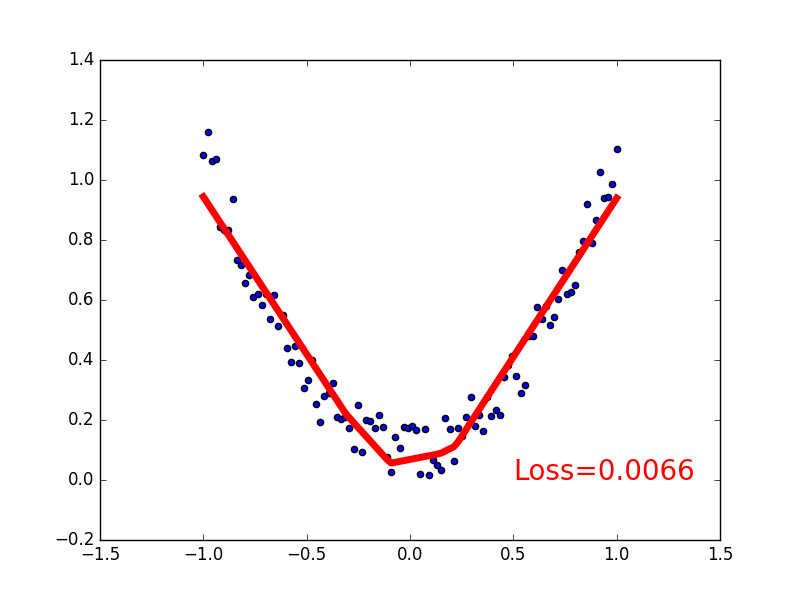
4.可视化训练过程
# optimizer 是训练的工具
optimizer = torch.optim.SGD(net.parameters(), lr=0.2) # 传入 net 的所有参数, 学习率
loss_func = torch.nn.MSELoss() # 预测值和真实值的误差计算公式 (均方差)
plt.ion() # 画图
plt.show()
for t in range(100):
prediction = net(x) # 喂给 net 训练数据 x, 输出预测值
loss = loss_func(prediction, y) # 计算两者的误差
optimizer.zero_grad() # 清空上一步的残余更新参数值
loss.backward() # 误差反向传播, 计算参数更新值
optimizer.step() # 将参数更新值施加到 net 的 parameters 上
# 接着上面来
if t % 5 == 0:
# plot and show learning process
plt.cla()
plt.scatter(x.data.numpy(), y.data.numpy())
plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
plt.text(0.5, 0, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color': 'red'})
plt.pause(0.1)
区分类型 (分类)
1.建立数据集
建立两个二次分布的数据, 不过他们的均值都不一样.
import torch
import matplotlib.pyplot as plt
# 假数据
n_data = torch.ones(100, 2) # 数据的基本形态
x0 = torch.normal(2*n_data, 1) # 类型0 x data (tensor), shape=(100, 2)
y0 = torch.zeros(100) # 类型0 y data (tensor), shape=(100, )
x1 = torch.normal(-2*n_data, 1) # 类型1 x data (tensor), shape=(100, 1)
y1 = torch.ones(100) # 类型1 y data (tensor), shape=(100, )
# 注意 x, y 数据的数据形式是一定要像下面一样 (torch.cat 是在合并数据)
x = torch.cat((x0, x1), 0).type(torch.FloatTensor) # FloatTensor = 32-bit floating
y = torch.cat((y0, y1), ).type(torch.LongTensor) # LongTensor = 64-bit integer
# 画图
plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=y.data.numpy(), s=100, lw=0, cmap='RdYlGn')
plt.show()
注意,如果用莫烦大神的画图代码,上面plt.scatter这段,会报错,因为画图x和y的数量不相同,x矩阵的形状是(200,2)的,而y矩阵的形状是(200),所以需要把x分成两部分来画图才可以的。
数据分布图如下:

2.建立神经网络
基本沿用上一个拟合关系的网络结构
import torch
import torch.nn.functional as F # 激励函数都在这
class Net(torch.nn.Module): # 继承 torch 的 Module
def __init__(self, n_feature, n_hidden, n_output):
super(Net, self).__init__() # 继承 __init__ 功能
self.hidden = torch.nn.Linear(n_feature, n_hidden) # 隐藏层线性输出
self.out = torch.nn.Linear(n_hidden, n_output) # 输出层线性输出
def forward(self, x):
# 正向传播输入值, 神经网络分析出输出值
x = F.relu(self.hidden(x)) # 激励函数(隐藏层的线性值)
x = self.out(x) # 输出值, 但是这个不是预测值, 预测值还需要再另外计算
return x
net = Net(n_feature=2, n_hidden=10, n_output=2) # 几个类别就几个 output
print(net) # net 的结构
"""
Net (
(hidden): Linear (2 -> 10)
(out): Linear (10 -> 2)
)
"""
输出如下:
Net(
(hidden): Linear(in_features=2, out_features=10, bias=True)
(out): Linear(in_features=10, out_features=2, bias=True)
)
'\nNet (\n (hidden): Linear (2 -> 10)\n (out): Linear (10 -> 2)\n)\n'
3.训练网络
# optimizer 是训练的工具
optimizer = torch.optim.SGD(net.parameters(), lr=0.02) # 传入 net 的所有参数, 学习率
# 算误差的时候, 注意真实值!不是! one-hot 形式的, 而是1D Tensor, (batch,)
# 但是预测值是2D tensor (batch, n_classes)
loss_func = torch.nn.CrossEntropyLoss()
for t in range(100):
out = net(x) # 喂给 net 训练数据 x, 输出分析值
loss = loss_func(out, y) # 计算两者的误差
optimizer.zero_grad() # 清空上一步的残余更新参数值
loss.backward() # 误差反向传播, 计算参数更新值
optimizer.step() # 将参数更新值施加到 net 的 parameters 上
4.可视化训练过程
# optimizer 是训练的工具
optimizer = torch.optim.SGD(net.parameters(), lr=0.02) # 传入 net 的所有参数, 学习率
# 算误差的时候, 注意真实值!不是! one-hot 形式的, 而是1D Tensor, (batch,)
# 但是预测值是2D tensor (batch, n_classes)
loss_func = torch.nn.CrossEntropyLoss()
for t in range(100):
out = net(x) # 喂给 net 训练数据 x, 输出分析值
loss = loss_func(out, y) # 计算两者的误差
optimizer.zero_grad() # 清空上一步的残余更新参数值
loss.backward() # 误差反向传播, 计算参数更新值
optimizer.step() # 将参数更新值施加到 net 的 parameters 上
# 接着上面来
if t % 2 == 0:
plt.cla()
# 过了一道 softmax 的激励函数后的最大概率才是预测值
prediction = torch.max(F.softmax(out), 1)[1]
pred_y = prediction.data.numpy().squeeze()
target_y = y.data.numpy()
plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=pred_y, s=100, lw=0, cmap='RdYlGn')
accuracy = sum(pred_y == target_y)/200. # 预测中有多少和真实值一样
plt.text(1.5, -4, 'Accuracy=%.2f' % accuracy, fontdict={'size': 20, 'color': 'red'})
plt.pause(0.1)
plt.ioff() # 停止画图
plt.show()
注意:
prediction=torch.max(F.softmax(out), 1) 中的1,表示【0,0,1】预测结果中,结果为1的结果的位置。
快速搭建
上一节用的方法更加底层,其实有更加快速的方法,对比一下就很清楚了:
Method 1
class Net(torch.nn.Module):
def __init__(self, n_feature, n_hidden, n_output):
super(Net, self).__init__()
self.hidden = torch.nn.Linear(n_feature, n_hidden)
self.predict = torch.nn.Linear(n_hidden, n_output)
def forward(self, x):
x = F.relu(self.hidden(x))
x = self.predict(x)
return x
net1 = Net(1, 10, 1) # 这是我们用这种方式搭建的 net1
Method 2
用nn库里一个函数就能快速搭建了,注意ReLU也算做一层加入到网络序列中。
net2 = torch.nn.Sequential(
torch.nn.Linear(1, 10),
torch.nn.ReLU(),
torch.nn.Linear(10, 1)
)
两种方法搭出来的模型都是一样的。
print(net1)
"""
Net (
(hidden): Linear (1 -> 10)
(predict): Linear (10 -> 1)
)
"""
print(net2)
"""
Sequential (
(0): Linear (1 -> 10)
(1): ReLU ()
(2): Linear (10 -> 1)
)
"""
Output:
Net(
(hidden): Linear(in_features=1, out_features=10, bias=True)
(predict): Linear(in_features=10, out_features=1, bias=True)
)
Sequential(
(0): Linear(in_features=1, out_features=10, bias=True)
(1): ReLU()
(2): Linear(in_features=10, out_features=1, bias=True)
)
'\nSequential (\n (0): Linear (1 -> 10)\n (1): ReLU ()\n (2): Linear (10 -> 1)\n)\n'
保存网络、参数
1.快速搭建网络
torch.manual_seed(1) # reproducible
# 假数据
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size()) # noisy y data (tensor), shape=(100, 1)
def save():
# 建网络
net1 = torch.nn.Sequential(
torch.nn.Linear(1, 10),
torch.nn.ReLU(),
torch.nn.Linear(10, 1)
)
optimizer = torch.optim.SGD(net1.parameters(), lr=0.2)
loss_func = torch.nn.MSELoss()
# 训练
for t in range(100):
prediction = net1(x)
loss = loss_func(prediction, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
有两种保存途径,保存整个网络包括参数 或 只保存参数不包括网络
torch.save(net1, 'net.pkl') # 保存整个网络
torch.save(net1.state_dict(), 'net_params.pkl') # 只保存网络中的参数 (速度快, 占内存少)
2.提取
两种保存途径对应两种提取方式:
(1)提取网络
这种方式将提取整个神经网络,网络大的时候可能会比较慢。
def restore_net():
# restore entire net1 to net2
net2 = torch.load('net.pkl')
prediction = net2(x)
(2)只提取网络参数
这种方式只提取所有的参数,然后再放到新建立的网络中。
def restore_params():
# 新建 net3
net3 = torch.nn.Sequential(
torch.nn.Linear(1, 10),
torch.nn.ReLU(),
torch.nn.Linear(10, 1)
)
# 将保存的参数复制到 net3
net3.load_state_dict(torch.load('net_params.pkl'))
prediction = net3(x)
查看三个网络模型的结果图:
import torch
import torch.nn.functional as F # 激励函数都在这
import matplotlib.pyplot as plt
torch.manual_seed(1) # reproducible
# 假数据
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size()) # noisy y data (tensor), shape=(100, 1)
def save():
# 建网络
net1 = torch.nn.Sequential(
torch.nn.Linear(1, 10),
torch.nn.ReLU(),
torch.nn.Linear(10, 1)
)
optimizer = torch.optim.SGD(net1.parameters(), lr=0.3)
loss_func = torch.nn.MSELoss()
# 训练
for t in range(100):
prediction = net1(x)
loss = loss_func(prediction, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
torch.save(net1, 'net.pkl') # 保存整个网络
torch.save(net1.state_dict(), 'net_params.pkl') # 只保存网络中的参数 (速度快, 占内存少)
# plot result
plt.figure(1, figsize=(10,3))
plt.subplot(131)
plt.title('Net1')
plt.scatter(x.data.numpy(), y.data.numpy())
plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
def restore_net():
# restore entire net1 to net2
net2 = torch.load('net.pkl')
prediction = net2(x)
# plot result
plt.figure(1, figsize=(10,3))
plt.subplot(132)
plt.title('Net2')
plt.scatter(x.data.numpy(), y.data.numpy())
plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
def restore_params():
# 新建 net3
net3 = torch.nn.Sequential(
torch.nn.Linear(1, 10),
torch.nn.ReLU(),
torch.nn.Linear(10, 1)
)
# 将保存的参数复制到 net3
net3.load_state_dict(torch.load('net_params.pkl'))
prediction = net3(x)
# plot result
plt.figure(1, figsize=(10,3))
plt.subplot(133)
plt.title('Net3')
plt.scatter(x.data.numpy(), y.data.numpy())
plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
# 保存 net1 (1. 整个网络, 2. 只有参数)
save()
# 提取整个网络
restore_net()
# 提取网络参数, 复制到新网络
restore_params()
plt.show()
批训练
进行批量训练需要用到一个很好用的工具DataLoader 。
1.DataLoader
注意,莫烦大神用的版本跟现在新版还是有些出入的,用Data.TensorDataset这个函数,不要指定data_tensor和target_tensor会报错的,因为新版的库改了,直接输入x和y就行了。
import torch
import torch.utils.data as Data
torch.manual_seed(1) # reproducible
BATCH_SIZE = 5 # 批训练的数据个数
x = torch.linspace(1, 10, 10) # x data (torch tensor)
y = torch.linspace(10, 1, 10) # y data (torch tensor)
# 先转换成 torch 能识别的 Dataset
torch_dataset = #Data.TensorDataset(data_tensor=x, target_tensor=y)
Data.TensorDataset(x, y)
# 把 dataset 放入 DataLoader
loader = Data.DataLoader(
dataset=torch_dataset, # torch TensorDataset format
batch_size=BATCH_SIZE, # mini batch size
shuffle=True, # 要不要打乱数据 (打乱比较好)
num_workers=2, # 多线程来读数据
)
for epoch in range(3): # 训练所有!整套!数据 3 次
for step, (batch_x, batch_y) in enumerate(loader): # 每一步 loader 释放一小批数据用来学习
# 假设这里就是你训练的地方...
# 打出来一些数据
print('Epoch: ', epoch, '| Step: ', step, '| batch x: ',
batch_x.numpy(), '| batch y: ', batch_y.numpy())
"""
Epoch: 0 | Step: 0 | batch x: [ 6. 7. 2. 3. 1.] | batch y: [ 5. 4. 9. 8. 10.]
Epoch: 0 | Step: 1 | batch x: [ 9. 10. 4. 8. 5.] | batch y: [ 2. 1. 7. 3. 6.]
Epoch: 1 | Step: 0 | batch x: [ 3. 4. 2. 9. 10.] | batch y: [ 8. 7. 9. 2. 1.]
Epoch: 1 | Step: 1 | batch x: [ 1. 7. 8. 5. 6.] | batch y: [ 10. 4. 3. 6. 5.]
Epoch: 2 | Step: 0 | batch x: [ 3. 9. 2. 6. 7.] | batch y: [ 8. 2. 9. 5. 4.]
Epoch: 2 | Step: 1 | batch x: [ 10. 4. 8. 1. 5.] | batch y: [ 1. 7. 3. 10. 6.]
"""
Optimizer 优化器
1.伪数据
import torch
import torch.utils.data as Data
import torch.nn.functional as F
import matplotlib.pyplot as plt
torch.manual_seed(1) # reproducible
LR = 0.01
BATCH_SIZE = 32
EPOCH = 12
# fake dataset
x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1)
y = x.pow(2) + 0.1*torch.normal(torch.zeros(*x.size()))
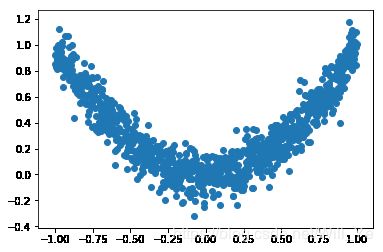
# plot dataset
plt.scatter(x.numpy(), y.numpy())
plt.show()
# 使用上节内容提到的 data loader
torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(dataset=torch_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=2,)
2.每个优化器优化一个神经网络
为了对比每一种优化器, 我们给他们各自创建一个神经网络, 但这个神经网络都来自同一个Net形式.
# 默认的 network 形式
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.hidden = torch.nn.Linear(1, 20) # hidden layer
self.predict = torch.nn.Linear(20, 1) # output layer
def forward(self, x):
x = F.relu(self.hidden(x)) # activation function for hidden layer
x = self.predict(x) # linear output
return x
# 为每个优化器创建一个 net
net_SGD = Net()
net_Momentum = Net()
net_RMSprop = Net()
net_Adam = Net()
nets = [net_SGD, net_Momentum, net_RMSprop, net_Adam]
3.优化器 Optimizer
接下来在创建不同的优化器, 用来训练不同的网络. 并创建一个 loss_func 用来计算误差. 我们用几种常见的优化器, SGD, Momentum, RMSprop, Adam.
# different optimizers
opt_SGD = torch.optim.SGD(net_SGD.parameters(), lr=LR)
opt_Momentum = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)
opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
opt_Adam = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
optimizers = [opt_SGD, opt_Momentum, opt_RMSprop, opt_Adam]
loss_func = torch.nn.MSELoss()
losses_his = [[], [], [], []] # 记录 training 时不同神经网络的 loss
4.训练/出图
for epoch in range(EPOCH):
print('Epoch: ', epoch)
for step, (b_x, b_y) in enumerate(loader):
# 对每个优化器, 优化属于他的神经网络
for net, opt, l_his in zip(nets, optimizers, losses_his):
output = net(b_x) # get output for every net
loss = loss_func(output, b_y) # compute loss for every net
opt.zero_grad() # clear gradients for next train
loss.backward() # backpropagation, compute gradients
opt.step() # apply gradients
l_his.append(loss.data.numpy()) # loss recoder
labels = ['SGD', 'Momentum', 'RMSprop', 'Adam']
for i, l_his in enumerate(losses_his):
plt.plot(l_his, label=labels[i])
plt.legend(loc='best')
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.ylim((0, 0.2))
plt.show()
Output:
Epoch: 0
Epoch: 1
Epoch: 2
Epoch: 3
Epoch: 4
Epoch: 5
Epoch: 6
Epoch: 7
Epoch: 8
Epoch: 9
Epoch: 10
Epoch: 11
import torch
import torch.utils.data as Data
import torch.nn.functional as F
import matplotlib.pyplot as plt
# torch.manual_seed(1) # reproducible
LR = 0.01
BATCH_SIZE = 32
EPOCH = 12
# fake dataset
x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1)
y = x.pow(2) + 0.1*torch.normal(torch.zeros(*x.size()))
# plot dataset
plt.scatter(x.numpy(), y.numpy())
plt.show()
# put dateset into torch dataset
torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(dataset=torch_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=2,)
# default network
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.hidden = torch.nn.Linear(1, 20) # hidden layer
self.predict = torch.nn.Linear(20, 1) # output layer
def forward(self, x):
x = F.relu(self.hidden(x)) # activation function for hidden layer
x = self.predict(x) # linear output
return x
if __name__ == '__main__':
# different nets
net_SGD = Net()
net_Momentum = Net()
net_RMSprop = Net()
net_Adam = Net()
nets = [net_SGD, net_Momentum, net_RMSprop, net_Adam]
# different optimizers
opt_SGD = torch.optim.SGD(net_SGD.parameters(), lr=LR)
opt_Momentum = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)
opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
opt_Adam = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
optimizers = [opt_SGD, opt_Momentum, opt_RMSprop, opt_Adam]
loss_func = torch.nn.MSELoss()
losses_his = [[], [], [], []] # record loss
# training
for epoch in range(EPOCH):
print('Epoch: ', epoch)
for step, (b_x, b_y) in enumerate(loader): # for each training step
for net, opt, l_his in zip(nets, optimizers, losses_his):
output = net(b_x) # get output for every net
loss = loss_func(output, b_y) # compute loss for every net
opt.zero_grad() # clear gradients for next train
loss.backward() # backpropagation, compute gradients
opt.step() # apply gradients
l_his.append(loss.data.numpy()) # loss recoder
labels = ['SGD', 'Momentum', 'RMSprop', 'Adam']
for i, l_his in enumerate(losses_his):
plt.plot(l_his, label=labels[i])
plt.legend(loc='best')
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.ylim((0, 0.2))
plt.show()
CNN卷积神经网络
1.MINIST手写数据
import torch
import torch.nn as nn
import torch.utils.data as Data
import torchvision # 数据库模块
import matplotlib.pyplot as plt
torch.manual_seed(1) # reproducible
# Hyper Parameters
EPOCH = 1 # 训练整批数据多少次, 为了节约时间, 我们只训练一次
BATCH_SIZE = 50
LR = 0.001 # 学习率
DOWNLOAD_MNIST = True # 如果你已经下载好了mnist数据就写上 False
# Mnist 手写数字
train_data = torchvision.datasets.MNIST(
root='./mnist/', # 保存或者提取位置
train=True, # this is training data
transform=torchvision.transforms.ToTensor(), # 转换 PIL.Image or numpy.ndarray 成
# torch.FloatTensor (C x H x W), 训练的时候 normalize 成 [0.0, 1.0] 区间
download=DOWNLOAD_MNIST, # 没下载就下载, 下载了就不用再下了
)
同样, 我们除了训练数据, 还给一些测试数据, 测试看看它有没有训练好.
test_data = torchvision.datasets.MNIST(root='./mnist/', train=False)
# 批训练 50samples, 1 channel, 28x28 (50, 1, 28, 28)
train_loader = Data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)
# 为了节约时间, 我们测试时只测试前2000个
test_x = torch.unsqueeze(test_data.test_data, dim=1).type(torch.FloatTensor)[:2000]/255. # shape from (2000, 28, 28) to (2000, 1, 28, 28), value in range(0,1)
test_y = test_data.test_labels[:2000]
2.CNN模型
和以前一样, 我们用一个 class 来建立 CNN 模型. 这个 CNN 整体流程是 卷积(Conv2d) -> 激励函数(ReLU) -> 池化, 向下采样 (MaxPooling) -> 再来一遍 -> 展平多维的卷积成的特征图 -> 接入全连接层 (Linear) -> 输出
class CNN(nn.Module):
def __init__(self):
super(CNN, self).__init__()
self.conv1 = nn.Sequential( # input shape (1, 28, 28)
nn.Conv2d(
in_channels=1, # input height
out_channels=16, # n_filters
kernel_size=5, # filter size
stride=1, # filter movement/step
padding=2, # 如果想要 con2d 出来的图片长宽没有变化, padding=(kernel_size-1)/2 当 stride=1
), # output shape (16, 28, 28)
nn.ReLU(), # activation
nn.MaxPool2d(kernel_size=2), # 在 2x2 空间里向下采样, output shape (16, 14, 14)
)
self.conv2 = nn.Sequential( # input shape (16, 14, 14)
nn.Conv2d(16, 32, 5, 1, 2), # output shape (32, 14, 14)
nn.ReLU(), # activation
nn.MaxPool2d(2), # output shape (32, 7, 7)
)
self.out = nn.Linear(32 * 7 * 7, 10) # fully connected layer, output 10 classes
def forward(self, x):
x = self.conv1(x)
x = self.conv2(x)
x = x.view(x.size(0), -1) # 展平多维的卷积图成 (batch_size, 32 * 7 * 7)
output = self.out(x)
return output
cnn = CNN()
print(cnn) # net architecture
"""
CNN (
(conv1): Sequential (
(0): Conv2d(1, 16, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(1): ReLU ()
(2): MaxPool2d (size=(2, 2), stride=(2, 2), dilation=(1, 1))
)
(conv2): Sequential (
(0): Conv2d(16, 32, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(1): ReLU ()
(2): MaxPool2d (size=(2, 2), stride=(2, 2), dilation=(1, 1))
)
(out): Linear (1568 -> 10)
)
"""
3.训练
下面我们开始训练, 将 x y 都用 Variable 包起来, 然后放入 cnn 中计算 output, 最后再计算误差.下面代码省略了计算精确度 accuracy 的部分。
optimizer = torch.optim.Adam(cnn.parameters(), lr=LR) # optimize all cnn parameters
loss_func = nn.CrossEntropyLoss() # the target label is not one-hotted
# training and testing
for epoch in range(EPOCH):
for step, (b_x, b_y) in enumerate(train_loader): # 分配 batch data, normalize x when iterate train_loader
output = cnn(b_x) # cnn output
loss = loss_func(output, b_y) # cross entropy loss
optimizer.zero_grad() # clear gradients for this training step
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
"""
...
Epoch: 0 | train loss: 0.0306 | test accuracy: 0.97
Epoch: 0 | train loss: 0.0147 | test accuracy: 0.98
Epoch: 0 | train loss: 0.0427 | test accuracy: 0.98
Epoch: 0 | train loss: 0.0078 | test accuracy: 0.98
"""
最后我们再来取10个数据, 看看预测的值到底对不对:
test_output = cnn(test_x[:10])
pred_y = torch.max(test_output, 1)[1].data.numpy().squeeze()
print(pred_y, 'prediction number')
print(test_y[:10].numpy(), 'real number')
"""
[7 2 1 0 4 1 4 9 5 9] prediction number
[7 2 1 0 4 1 4 9 5 9] real number
"""
4.可视化训练(视频中没有)
可视化的代码主要是用 matplotlib 和 sklearn 来完成的, 因为其中我们用到了 T-SNE 的降维手段, 将高维的 CNN 最后一层输出结果可视化, 也就是 CNN forward 代码中的 x = x.view(x.size(0), -1) 这一个结果.
完整代码:
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import numpy as np
import matplotlib.pyplot as plt
tf.set_random_seed(1)
np.random.seed(1)
BATCH_SIZE = 50
LR = 0.001 # learning rate
mnist = input_data.read_data_sets('./mnist', one_hot=True) # they has been normalized to range (0,1)
test_x = mnist.test.images[:2000]
test_y = mnist.test.labels[:2000]
# plot one example
print(mnist.train.images.shape) # (55000, 28 * 28)
print(mnist.train.labels.shape) # (55000, 10)
plt.imshow(mnist.train.images[0].reshape((28, 28)), cmap='gray')
plt.title('%i' % np.argmax(mnist.train.labels[0])); plt.show()
tf_x = tf.placeholder(tf.float32, [None, 28*28]) / 255.
image = tf.reshape(tf_x, [-1, 28, 28, 1]) # (batch, height, width, channel)
tf_y = tf.placeholder(tf.int32, [None, 10]) # input y
# CNN
conv1 = tf.layers.conv2d( # shape (28, 28, 1)
inputs=image,
filters=16,
kernel_size=5,
strides=1,
padding='same',
activation=tf.nn.relu
) # -> (28, 28, 16)
pool1 = tf.layers.max_pooling2d(
conv1,
pool_size=2,
strides=2,
) # -> (14, 14, 16)
conv2 = tf.layers.conv2d(pool1, 32, 5, 1, 'same', activation=tf.nn.relu) # -> (14, 14, 32)
pool2 = tf.layers.max_pooling2d(conv2, 2, 2) # -> (7, 7, 32)
flat = tf.reshape(pool2, [-1, 7*7*32]) # -> (7*7*32, )
output = tf.layers.dense(flat, 10) # output layer
loss = tf.losses.softmax_cross_entropy(onehot_labels=tf_y, logits=output) # compute cost
train_op = tf.train.AdamOptimizer(LR).minimize(loss)
accuracy = tf.metrics.accuracy( # return (acc, update_op), and create 2 local variables
labels=tf.argmax(tf_y, axis=1), predictions=tf.argmax(output, axis=1),)[1]
sess = tf.Session()
init_op = tf.group(tf.global_variables_initializer(), tf.local_variables_initializer()) # the local var is for accuracy_op
sess.run(init_op) # initialize var in graph
# following function (plot_with_labels) is for visualization, can be ignored if not interested
from matplotlib import cm
try: from sklearn.manifold import TSNE; HAS_SK = True
except: HAS_SK = False; print('\nPlease install sklearn for layer visualization\n')
def plot_with_labels(lowDWeights, labels):
plt.cla(); X, Y = lowDWeights[:, 0], lowDWeights[:, 1]
for x, y, s in zip(X, Y, labels):
c = cm.rainbow(int(255 * s / 9)); plt.text(x, y, s, backgroundcolor=c, fontsize=9)
plt.xlim(X.min(), X.max()); plt.ylim(Y.min(), Y.max()); plt.title('Visualize last layer'); plt.show(); plt.pause(0.01)
plt.ion()
for step in range(600):
b_x, b_y = mnist.train.next_batch(BATCH_SIZE)
_, loss_ = sess.run([train_op, loss], {tf_x: b_x, tf_y: b_y})
if step % 50 == 0:
accuracy_, flat_representation = sess.run([accuracy, flat], {tf_x: test_x, tf_y: test_y})
print('Step:', step, '| train loss: %.4f' % loss_, '| test accuracy: %.2f' % accuracy_)
if HAS_SK:
# Visualization of trained flatten layer (T-SNE)
tsne = TSNE(perplexity=30, n_components=2, init='pca', n_iter=5000); plot_only = 500
low_dim_embs = tsne.fit_transform(flat_representation[:plot_only, :])
labels = np.argmax(test_y, axis=1)[:plot_only]; plot_with_labels(low_dim_embs, labels)
plt.ioff()
# print 10 predictions from test data
test_output = sess.run(output, {tf_x: test_x[:10]})
pred_y = np.argmax(test_output, 1)
print(pred_y, 'prediction number')
print(np.argmax(test_y[:10], 1), 'real number')
RNN循环神经网络
1.MNIST手写数据
import torch
from torch import nn
import torchvision.datasets as dsets
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
torch.manual_seed(1) # reproducible
# Hyper Parameters
EPOCH = 1 # 训练整批数据多少次, 为了节约时间, 我们只训练一次
BATCH_SIZE = 64
TIME_STEP = 28 # rnn 时间步数 / 图片高度
INPUT_SIZE = 28 # rnn 每步输入值 / 图片每行像素
LR = 0.01 # learning rate
DOWNLOAD_MNIST = True # 如果你已经下载好了mnist数据就写上 Fasle
# Mnist 手写数字
train_data = torchvision.datasets.MNIST(
root='./mnist/', # 保存或者提取位置
train=True, # this is training data
transform=torchvision.transforms.ToTensor(), # 转换 PIL.Image or numpy.ndarray 成
# torch.FloatTensor (C x H x W), 训练的时候 normalize 成 [0.0, 1.0] 区间
download=DOWNLOAD_MNIST, # 没下载就下载, 下载了就不用再下了
)
测试集:
test_data = torchvision.datasets.MNIST(root='./mnist/', train=False)
# 批训练 50samples, 1 channel, 28x28 (50, 1, 28, 28)
train_loader = Data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)
# 为了节约时间, 我们测试时只测试前2000个
test_x = torch.unsqueeze(test_data.test_data, dim=1).type(torch.FloatTensor)[:2000]/255. # shape from (2000, 28, 28) to (2000, 1, 28, 28), value in range(0,1)
test_y = test_data.test_labels[:2000]
2.RNN模型
和以前一样, 我们用一个 class 来建立 RNN 模型. 这个 RNN 整体流程是
(input0, state0)->LSTM->(output0, state1);(input1, state1)->LSTM->(output1, state2);- …
(inputN, stateN)->LSTM->(outputN, stateN+1);outputN->Linear->prediction. 通过LSTM分析每一时刻的值, 并且将这一时刻和前面时刻的理解合并在一起, 生成当前时刻对前面数据的理解或记忆. 传递这种理解给下一时刻分析.
class RNN(nn.Module):
def __init__(self):
super(RNN, self).__init__()
self.rnn = nn.LSTM( # LSTM 效果要比 nn.RNN() 好多了
input_size=28, # 图片每行的数据像素点
hidden_size=64, # rnn hidden unit
num_layers=1, # 有几层 RNN layers
batch_first=True, # input & output 会是以 batch size 为第一维度的特征集 e.g. (batch, time_step, input_size)
)
self.out = nn.Linear(64, 10) # 输出层
def forward(self, x):
# x shape (batch, time_step, input_size)
# r_out shape (batch, time_step, output_size)
# h_n shape (n_layers, batch, hidden_size) LSTM 有两个 hidden states, h_n 是分线, h_c 是主线
# h_c shape (n_layers, batch, hidden_size)
r_out, (h_n, h_c) = self.rnn(x, None) # None 表示 hidden state 会用全0的 state
# 选取最后一个时间点的 r_out 输出
# 这里 r_out[:, -1, :] 的值也是 h_n 的值
out = self.out(r_out[:, -1, :])
return out
rnn = RNN()
print(rnn)
"""
RNN (
(rnn): LSTM(28, 64, batch_first=True)
(out): Linear (64 -> 10)
)
"""
3.训练
我们将图片数据看成一个时间上的连续数据, 每一行的像素点都是这个时刻的输入, 读完整张图片就是从上而下的读完了每行的像素点. 然后我们就可以拿出 RNN 在最后一步的分析值判断图片是哪一类了. 下面的代码省略了计算 accuracy 的部分,
optimizer = torch.optim.Adam(rnn.parameters(), lr=LR) # optimize all parameters
loss_func = nn.CrossEntropyLoss() # the target label is not one-hotted
# training and testing
for epoch in range(EPOCH):
for step, (x, b_y) in enumerate(train_loader): # gives batch data
b_x = x.view(-1, 28, 28) # reshape x to (batch, time_step, input_size)
output = rnn(b_x) # rnn output
loss = loss_func(output, b_y) # cross entropy loss
optimizer.zero_grad() # clear gradients for this training step
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
"""
...
Epoch: 0 | train loss: 0.0945 | test accuracy: 0.94
Epoch: 0 | train loss: 0.0984 | test accuracy: 0.94
Epoch: 0 | train loss: 0.0332 | test accuracy: 0.95
Epoch: 0 | train loss: 0.1868 | test accuracy: 0.96
"""
最后我们再来取10个数据, 看看预测的值到底对不对:
test_output = rnn(test_x[:10].view(-1, 28, 28))
pred_y = torch.max(test_output, 1)[1].data.numpy().squeeze()
print(pred_y, 'prediction number')
print(test_y[:10], 'real number')
"""
[7 2 1 0 4 1 4 9 5 9] prediction number
[7 2 1 0 4 1 4 9 5 9] real number
"""
完整代码:
import torch
from torch import nn
import torchvision.datasets as dsets
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
# torch.manual_seed(1) # reproducible
# Hyper Parameters
EPOCH = 1 # train the training data n times, to save time, we just train 1 epoch
BATCH_SIZE = 64
TIME_STEP = 28 # rnn time step / image height
INPUT_SIZE = 28 # rnn input size / image width
LR = 0.01 # learning rate
DOWNLOAD_MNIST = True # set to True if haven't download the data
# Mnist digital dataset
train_data = dsets.MNIST(
root='./mnist/',
train=True, # this is training data
transform=transforms.ToTensor(), # Converts a PIL.Image or numpy.ndarray to
# torch.FloatTensor of shape (C x H x W) and normalize in the range [0.0, 1.0]
download=DOWNLOAD_MNIST, # download it if you don't have it
)
# plot one example
print(train_data.train_data.size()) # (60000, 28, 28)
print(train_data.train_labels.size()) # (60000)
plt.imshow(train_data.train_data[0].numpy(), cmap='gray')
plt.title('%i' % train_data.train_labels[0])
plt.show()
# Data Loader for easy mini-batch return in training
train_loader = torch.utils.data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)
# convert test data into Variable, pick 2000 samples to speed up testing
test_data = dsets.MNIST(root='./mnist/', train=False, transform=transforms.ToTensor())
test_x = test_data.test_data.type(torch.FloatTensor)[:2000]/255. # shape (2000, 28, 28) value in range(0,1)
test_y = test_data.test_labels.numpy()[:2000] # covert to numpy array
class RNN(nn.Module):
def __init__(self):
super(RNN, self).__init__()
self.rnn = nn.LSTM( # if use nn.RNN(), it hardly learns
input_size=INPUT_SIZE,
hidden_size=64, # rnn hidden unit
num_layers=1, # number of rnn layer
batch_first=True, # input & output will has batch size as 1s dimension. e.g. (batch, time_step, input_size)
)
self.out = nn.Linear(64, 10)
def forward(self, x):
# x shape (batch, time_step, input_size)
# r_out shape (batch, time_step, output_size)
# h_n shape (n_layers, batch, hidden_size)
# h_c shape (n_layers, batch, hidden_size)
r_out, (h_n, h_c) = self.rnn(x, None) # None represents zero initial hidden state
# choose r_out at the last time step
out = self.out(r_out[:, -1, :])
return out
rnn = RNN()
print(rnn)
optimizer = torch.optim.Adam(rnn.parameters(), lr=LR) # optimize all cnn parameters
loss_func = nn.CrossEntropyLoss() # the target label is not one-hotted
# training and testing
for epoch in range(EPOCH):
for step, (b_x, b_y) in enumerate(train_loader): # gives batch data
b_x = b_x.view(-1, 28, 28) # reshape x to (batch, time_step, input_size)
output = rnn(b_x) # rnn output
loss = loss_func(output, b_y) # cross entropy loss
optimizer.zero_grad() # clear gradients for this training step
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
if step % 50 == 0:
test_output = rnn(test_x) # (samples, time_step, input_size)
pred_y = torch.max(test_output, 1)[1].data.numpy()
accuracy = float((pred_y == test_y).astype(int).sum()) / float(test_y.size)
print('Epoch: ', epoch, '| train loss: %.4f' % loss.data.numpy(), '| test accuracy: %.2f' % accuracy)
# print 10 predictions from test data
test_output = rnn(test_x[:10].view(-1, 28, 28))
pred_y = torch.max(test_output, 1)[1].data.numpy()
print(pred_y, 'prediction number')
print(test_y[:10], 'real number')
RNN部分就不细究了,平时基本用不上,以后用的时候再补充心得
RNN循环神经网络(回归)
1.训练数据
我们要用到的数据就是这样的一些数据, 我们想要用 sin 的曲线预测出 cos 的曲线.

import torch
from torch import nn
import numpy as np
import matplotlib.pyplot as plt
torch.manual_seed(1) # reproducible
# Hyper Parameters
TIME_STEP = 10 # rnn time step / image height
INPUT_SIZE = 1 # rnn input size / image width
LR = 0.02 # learning rate
DOWNLOAD_MNIST = False # set to True if haven't download the data
2.RNN模型
这一次的 RNN, 我们对每一个 r_out 都得放到 Linear 中去计算出预测的 output, 所以我们能用一个 for loop 来循环计算. 这点是 Tensorflow 望尘莫及的! 除了这点, 还有动态的过程。
class RNN(nn.Module):
def __init__(self):
super(RNN, self).__init__()
self.rnn = nn.RNN( # 这回一个普通的 RNN 就能胜任
input_size=1,
hidden_size=32, # rnn hidden unit
num_layers=1, # 有几层 RNN layers
batch_first=True, # input & output 会是以 batch size 为第一维度的特征集 e.g. (batch, time_step, input_size)
)
self.out = nn.Linear(32, 1)
def forward(self, x, h_state): # 因为 hidden state 是连续的, 所以我们要一直传递这一个 state
# x (batch, time_step, input_size)
# h_state (n_layers, batch, hidden_size)
# r_out (batch, time_step, output_size)
r_out, h_state = self.rnn(x, h_state) # h_state 也要作为 RNN 的一个输入
outs = [] # 保存所有时间点的预测值
for time_step in range(r_out.size(1)): # 对每一个时间点计算 output
outs.append(self.out(r_out[:, time_step, :]))
return torch.stack(outs, dim=1), h_state
rnn = RNN()
print(rnn)
"""
RNN (
(rnn): RNN(1, 32, batch_first=True)
(out): Linear (32 -> 1)
)
"""
其实熟悉 RNN 的朋友应该知道, forward 过程中的对每个时间点求输出还有一招使得计算量比较小的. 不过上面的内容主要是为了呈现 PyTorch 在动态构图上的优势, 所以我用了一个 for loop 来搭建那套输出系统. 下面介绍一个替换方式. 使用 reshape 的方式整批计算.
def forward(self, x, h_state):
r_out, h_state = self.rnn(x, h_state)
r_out = r_out.view(-1, 32)
outs = self.out(r_out)
return outs.view(-1, 32, TIME_STEP), h_state
3.训练
下面的代码就能实现动图的效果啦~开心, 可以看出, 我们使用 x 作为输入的 sin 值, 然后 y 作为想要拟合的输出, cos 值. 因为他们两条曲线是存在某种关系的, 所以我们就能用 sin 来预测 cos. rnn 会理解他们的关系, 并用里面的参数分析出来这个时刻 sin 曲线上的点如何对应上 cos 曲线上的点.

optimizer = torch.optim.Adam(rnn.parameters(), lr=LR) # optimize all rnn parameters
loss_func = nn.MSELoss()
h_state = None # 要使用初始 hidden state, 可以设成 None
for step in range(100):
start, end = step * np.pi, (step+1)*np.pi # time steps
# sin 预测 cos
steps = np.linspace(start, end, 10, dtype=np.float32)
x_np = np.sin(steps) # float32 for converting torch FloatTensor
y_np = np.cos(steps)
x = torch.from_numpy(x_np[np.newaxis, :, np.newaxis]) # shape (batch, time_step, input_size)
y = torch.from_numpy(y_np[np.newaxis, :, np.newaxis])
prediction, h_state = rnn(x, h_state) # rnn 对于每个 step 的 prediction, 还有最后一个 step 的 h_state
# !! 下一步十分重要 !!
h_state = h_state.data # 要把 h_state 重新包装一下才能放入下一个 iteration, 不然会报错
loss = loss_func(prediction, y) # cross entropy loss
optimizer.zero_grad() # clear gradients for this training step
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
import torch
from torch import nn
import numpy as np
import matplotlib.pyplot as plt
# torch.manual_seed(1) # reproducible
# Hyper Parameters
TIME_STEP = 10 # rnn time step
INPUT_SIZE = 1 # rnn input size
LR = 0.02 # learning rate
# show data
steps = np.linspace(0, np.pi*2, 100, dtype=np.float32) # float32 for converting torch FloatTensor
x_np = np.sin(steps)
y_np = np.cos(steps)
plt.plot(steps, y_np, 'r-', label='target (cos)')
plt.plot(steps, x_np, 'b-', label='input (sin)')
plt.legend(loc='best')
plt.show()
class RNN(nn.Module):
def __init__(self):
super(RNN, self).__init__()
self.rnn = nn.RNN(
input_size=INPUT_SIZE,
hidden_size=32, # rnn hidden unit
num_layers=1, # number of rnn layer
batch_first=True, # input & output will has batch size as 1s dimension. e.g. (batch, time_step, input_size)
)
self.out = nn.Linear(32, 1)
def forward(self, x, h_state):
# x (batch, time_step, input_size)
# h_state (n_layers, batch, hidden_size)
# r_out (batch, time_step, hidden_size)
r_out, h_state = self.rnn(x, h_state)
outs = [] # save all predictions
for time_step in range(r_out.size(1)): # calculate output for each time step
outs.append(self.out(r_out[:, time_step, :]))
return torch.stack(outs, dim=1), h_state
# instead, for simplicity, you can replace above codes by follows
# r_out = r_out.view(-1, 32)
# outs = self.out(r_out)
# outs = outs.view(-1, TIME_STEP, 1)
# return outs, h_state
# or even simpler, since nn.Linear can accept inputs of any dimension
# and returns outputs with same dimension except for the last
# outs = self.out(r_out)
# return outs
rnn = RNN()
print(rnn)
optimizer = torch.optim.Adam(rnn.parameters(), lr=LR) # optimize all cnn parameters
loss_func = nn.MSELoss()
h_state = None # for initial hidden state
plt.figure(1, figsize=(12, 5))
plt.ion() # continuously plot
for step in range(100):
start, end = step * np.pi, (step+1)*np.pi # time range
# use sin predicts cos
steps = np.linspace(start, end, TIME_STEP, dtype=np.float32, endpoint=False) # float32 for converting torch FloatTensor
x_np = np.sin(steps)
y_np = np.cos(steps)
x = torch.from_numpy(x_np[np.newaxis, :, np.newaxis]) # shape (batch, time_step, input_size)
y = torch.from_numpy(y_np[np.newaxis, :, np.newaxis])
prediction, h_state = rnn(x, h_state) # rnn output
# !! next step is important !!
h_state = h_state.data # repack the hidden state, break the connection from last iteration
loss = loss_func(prediction, y) # calculate loss
optimizer.zero_grad() # clear gradients for this training step
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
# plotting
plt.plot(steps, y_np.flatten(), 'r-')
plt.plot(steps, prediction.data.numpy().flatten(), 'b-')
plt.draw(); plt.pause(0.05)
plt.ioff()
plt.show()
AutoEncoder (自编码/非监督学习)
神经网络也能进行非监督学习, 只需要训练数据, 不需要标签数据. 自编码就是这样一种形式. 自编码能自动分类数据, 而且也能嵌套在半监督学习的上面, 用少量的有标签样本和大量的无标签样本学习.
这次我们还用 MNIST 手写数字数据来压缩再解压图片.

然后用压缩的特征进行非监督分类.
1.训练数据
自编码只用训练集就好了, 而且只需要训练 training data 的 image, 不用训练 labels.
import torch
import torch.nn as nn
import torch.utils.data as Data
import torchvision
# 超参数
EPOCH = 10
BATCH_SIZE = 64
LR = 0.005
DOWNLOAD_MNIST = True # 下过数据的话, 就可以设置成 False
N_TEST_IMG = 5 # 到时候显示 5张图片看效果, 如上图一
# Mnist digits dataset
train_data = torchvision.datasets.MNIST(
root='./mnist/',
train=True, # this is training data
transform=torchvision.transforms.ToTensor(), # Converts a PIL.Image or numpy.ndarray to
# torch.FloatTensor of shape (C x H x W) and normalize in the range [0.0, 1.0]
download=DOWNLOAD_MNIST, # download it if you don't have it
)
2.AutoEncoder
AutoEncoder 形式很简单, 分别是 encoder 和 decoder, 压缩和解压, 压缩后得到压缩的特征值, 再从压缩的特征值解压成原图片.
class AutoEncoder(nn.Module):
def __init__(self):
super(AutoEncoder, self).__init__()
# 压缩
self.encoder = nn.Sequential(
nn.Linear(28*28, 128),
nn.Tanh(),
nn.Linear(128, 64),
nn.Tanh(),
nn.Linear(64, 12),
nn.Tanh(),
nn.Linear(12, 3), # 压缩成3个特征, 进行 3D 图像可视化
)
# 解压
self.decoder = nn.Sequential(
nn.Linear(3, 12),
nn.Tanh(),
nn.Linear(12, 64),
nn.Tanh(),
nn.Linear(64, 128),
nn.Tanh(),
nn.Linear(128, 28*28),
nn.Sigmoid(), # 激励函数让输出值在 (0, 1)
)
def forward(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return encoded, decoded
autoencoder = AutoEncoder()
3.训练
训练, 并可视化训练的过程. 我们可以有效的利用 encoder 和 decoder 来做很多事, 比如这里我们用 decoder 的信息输出看和原图片的对比, 还能用 encoder 来看经过压缩后, 神经网络对原图片的理解. encoder 能将不同图片数据大概的分离开来. 这样就是一个无监督学习的过程.
optimizer = torch.optim.Adam(autoencoder.parameters(), lr=LR)
loss_func = nn.MSELoss()
for epoch in range(EPOCH):
for step, (x, b_label) in enumerate(train_loader):
b_x = x.view(-1, 28*28) # batch x, shape (batch, 28*28)
b_y = x.view(-1, 28*28) # batch y, shape (batch, 28*28)
encoded, decoded = autoencoder(b_x)
loss = loss_func(decoded, b_y) # mean square error
optimizer.zero_grad() # clear gradients for this training step
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
4.画3D图
3D 的可视化图挺有趣的, 还能挪动观看, 更加直观, 好理解.
# 要观看的数据
view_data = train_data.train_data[:200].view(-1, 28*28).type(torch.FloatTensor)/255.
encoded_data, _ = autoencoder(view_data) # 提取压缩的特征值
fig = plt.figure(2)
ax = Axes3D(fig) # 3D 图
# x, y, z 的数据值
X = encoded_data.data[:, 0].numpy()
Y = encoded_data.data[:, 1].numpy()
Z = encoded_data.data[:, 2].numpy()
values = train_data.train_labels[:200].numpy() # 标签值
for x, y, z, s in zip(X, Y, Z, values):
c = cm.rainbow(int(255*s/9)) # 上色
ax.text(x, y, z, s, backgroundcolor=c) # 标位子
ax.set_xlim(X.min(), X.max())
ax.set_ylim(Y.min(), Y.max())
ax.set_zlim(Z.min(), Z.max())
plt.show()
完整代码:
import torch
import torch.nn as nn
import torch.utils.data as Data
import torchvision
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import numpy as np
# torch.manual_seed(1) # reproducible
# Hyper Parameters
EPOCH = 10
BATCH_SIZE = 64
LR = 0.005 # learning rate
DOWNLOAD_MNIST = False
N_TEST_IMG = 5
# Mnist digits dataset
train_data = torchvision.datasets.MNIST(
root='./mnist/',
train=True, # this is training data
transform=torchvision.transforms.ToTensor(), # Converts a PIL.Image or numpy.ndarray to
# torch.FloatTensor of shape (C x H x W) and normalize in the range [0.0, 1.0]
download=DOWNLOAD_MNIST, # download it if you don't have it
)
# plot one example
print(train_data.train_data.size()) # (60000, 28, 28)
print(train_data.train_labels.size()) # (60000)
plt.imshow(train_data.train_data[2].numpy(), cmap='gray')
plt.title('%i' % train_data.train_labels[2])
plt.show()
# Data Loader for easy mini-batch return in training, the image batch shape will be (50, 1, 28, 28)
train_loader = Data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)
class AutoEncoder(nn.Module):
def __init__(self):
super(AutoEncoder, self).__init__()
self.encoder = nn.Sequential(
nn.Linear(28*28, 128),
nn.Tanh(),
nn.Linear(128, 64),
nn.Tanh(),
nn.Linear(64, 12),
nn.Tanh(),
nn.Linear(12, 3), # compress to 3 features which can be visualized in plt
)
self.decoder = nn.Sequential(
nn.Linear(3, 12),
nn.Tanh(),
nn.Linear(12, 64),
nn.Tanh(),
nn.Linear(64, 128),
nn.Tanh(),
nn.Linear(128, 28*28),
nn.Sigmoid(), # compress to a range (0, 1)
)
def forward(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return encoded, decoded
autoencoder = AutoEncoder()
optimizer = torch.optim.Adam(autoencoder.parameters(), lr=LR)
loss_func = nn.MSELoss()
# initialize figure
f, a = plt.subplots(2, N_TEST_IMG, figsize=(5, 2))
plt.ion() # continuously plot
# original data (first row) for viewing
view_data = train_data.train_data[:N_TEST_IMG].view(-1, 28*28).type(torch.FloatTensor)/255.
for i in range(N_TEST_IMG):
a[0][i].imshow(np.reshape(view_data.data.numpy()[i], (28, 28)), cmap='gray'); a[0][i].set_xticks(()); a[0][i].set_yticks(())
for epoch in range(EPOCH):
for step, (x, b_label) in enumerate(train_loader):
b_x = x.view(-1, 28*28) # batch x, shape (batch, 28*28)
b_y = x.view(-1, 28*28) # batch y, shape (batch, 28*28)
encoded, decoded = autoencoder(b_x)
loss = loss_func(decoded, b_y) # mean square error
optimizer.zero_grad() # clear gradients for this training step
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
if step % 100 == 0:
print('Epoch: ', epoch, '| train loss: %.4f' % loss.data.numpy())
# plotting decoded image (second row)
_, decoded_data = autoencoder(view_data)
for i in range(N_TEST_IMG):
a[1][i].clear()
a[1][i].imshow(np.reshape(decoded_data.data.numpy()[i], (28, 28)), cmap='gray')
a[1][i].set_xticks(()); a[1][i].set_yticks(())
plt.draw(); plt.pause(0.05)
plt.ioff()
plt.show()
# visualize in 3D plot
view_data = train_data.train_data[:200].view(-1, 28*28).type(torch.FloatTensor)/255.
encoded_data, _ = autoencoder(view_data)
fig = plt.figure(2); ax = Axes3D(fig)
X, Y, Z = encoded_data.data[:, 0].numpy(), encoded_data.data[:, 1].numpy(), encoded_data.data[:, 2].numpy()
values = train_data.train_labels[:200].numpy()
for x, y, z, s in zip(X, Y, Z, values):
c = cm.rainbow(int(255*s/9)); ax.text(x, y, z, s, backgroundcolor=c)
ax.set_xlim(X.min(), X.max()); ax.set_ylim(Y.min(), Y.max()); ax.set_zlim(Z.min(), Z.max())
plt.show()
GPU加速
最想写的一部分,太重要太好用了。注意要加.cuda()的地方,换汤不换药,照葫芦画瓢即可。
import torch
import torch.nn as nn
import torch.utils.data as Data
import torchvision
# torch.manual_seed(1)
EPOCH = 1
BATCH_SIZE = 50
LR = 0.001
DOWNLOAD_MNIST = False
train_data = torchvision.datasets.MNIST(root='./mnist/', train=True, transform=torchvision.transforms.ToTensor(), download=DOWNLOAD_MNIST,)
train_loader = Data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)
test_data = torchvision.datasets.MNIST(root='./mnist/', train=False)
# !!!!!!!! Change in here !!!!!!!!! #
test_x = torch.unsqueeze(test_data.test_data, dim=1).type(torch.FloatTensor)[:2000].cuda()/255. # Tensor on GPU
test_y = test_data.test_labels[:2000].cuda()
class CNN(nn.Module):
def __init__(self):
super(CNN, self).__init__()
self.conv1 = nn.Sequential(nn.Conv2d(in_channels=1, out_channels=16, kernel_size=5, stride=1, padding=2,),
nn.ReLU(), nn.MaxPool2d(kernel_size=2),)
self.conv2 = nn.Sequential(nn.Conv2d(16, 32, 5, 1, 2), nn.ReLU(), nn.MaxPool2d(2),)
self.out = nn.Linear(32 * 7 * 7, 10)
def forward(self, x):
x = self.conv1(x)
x = self.conv2(x)
x = x.view(x.size(0), -1)
output = self.out(x)
return output
cnn = CNN()
# !!!!!!!! Change in here !!!!!!!!! #
cnn.cuda() # Moves all model parameters and buffers to the GPU.
optimizer = torch.optim.Adam(cnn.parameters(), lr=LR)
loss_func = nn.CrossEntropyLoss()
for epoch in range(EPOCH):
for step, (x, y) in enumerate(train_loader):
# !!!!!!!! Change in here !!!!!!!!! #
b_x = x.cuda() # Tensor on GPU
b_y = y.cuda() # Tensor on GPU
output = cnn(b_x)
loss = loss_func(output, b_y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if step % 50 == 0:
test_output = cnn(test_x)
# !!!!!!!! Change in here !!!!!!!!! #
pred_y = torch.max(test_output, 1)[1].cuda().data # move the computation in GPU
accuracy = torch.sum(pred_y == test_y).type(torch.FloatTensor) / test_y.size(0)
print('Epoch: ', epoch, '| train loss: %.4f' % loss.data.cpu().numpy(), '| test accuracy: %.2f' % accuracy)
test_output = cnn(test_x[:10])
# !!!!!!!! Change in here !!!!!!!!! #
pred_y = torch.max(test_output, 1)[1].cuda().data # move the computation in GPU
print(pred_y, 'prediction number')
print(test_y[:10], 'real number')
转移至CPU
有些计算要在CPU上进行的,比如plt的可视化
cpu_data = gpu_data.cpu()
Dropout缓解过拟合
1.做点数据
自己做一些伪数据, 用来模拟真实情况. 数据少, 才能凸显过拟合问题, 所以我们就做10个数据点.

import torch
import matplotlib.pyplot as plt
torch.manual_seed(1) # reproducible
N_SAMPLES = 20
N_HIDDEN = 300
# training data
x = torch.unsqueeze(torch.linspace(-1, 1, N_SAMPLES), 1)
y = x + 0.3*torch.normal(torch.zeros(N_SAMPLES, 1), torch.ones(N_SAMPLES, 1))
# test data
test_x = torch.unsqueeze(torch.linspace(-1, 1, N_SAMPLES), 1)
test_y = test_x + 0.3*torch.normal(torch.zeros(N_SAMPLES, 1), torch.ones(N_SAMPLES, 1))
# show data
plt.scatter(x.data.numpy(), y.data.numpy(), c='magenta', s=50, alpha=0.5, label='train')
plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='cyan', s=50, alpha=0.5, label='test')
plt.legend(loc='upper left')
plt.ylim((-2.5, 2.5))
plt.show()
2.搭建神经网络
我们在这里搭建两个神经网络, 一个没有dropout一个有 dropout. 没有 dropout 的容易出现 过拟合, 那我们就命名为 net_overfitting, 另一个就是 net_dropped. torch.nn.Dropout(0.5) 这里的 0.5 指的是随机有 50% 的神经元会被关闭/丢弃.
关键就在于设置隐藏层和激活函数之间加多一个dropout.
net_overfitting = torch.nn.Sequential(
torch.nn.Linear(1, N_HIDDEN),
torch.nn.ReLU(),
torch.nn.Linear(N_HIDDEN, N_HIDDEN),
torch.nn.ReLU(),
torch.nn.Linear(N_HIDDEN, 1),
)
net_dropped = torch.nn.Sequential(
torch.nn.Linear(1, N_HIDDEN),
torch.nn.Dropout(0.5), # drop 50% of the neuron
torch.nn.ReLU(),
torch.nn.Linear(N_HIDDEN, N_HIDDEN),
torch.nn.Dropout(0.5), # drop 50% of the neuron
torch.nn.ReLU(),
torch.nn.Linear(N_HIDDEN, 1),
)
3.训练
训练的时候, 这两个神经网络分开训练. 训练的环境都一样.
optimizer_ofit = torch.optim.Adam(net_overfitting.parameters(), lr=0.01)
optimizer_drop = torch.optim.Adam(net_dropped.parameters(), lr=0.01)
loss_func = torch.nn.MSELoss()
for t in range(500):
pred_ofit = net_overfitting(x)
pred_drop = net_dropped(x)
loss_ofit = loss_func(pred_ofit, y)
loss_drop = loss_func(pred_drop, y)
optimizer_ofit.zero_grad()
optimizer_drop.zero_grad()
loss_ofit.backward()
loss_drop.backward()
optimizer_ofit.step()
optimizer_drop.step()
4.对比测试结果
在这个 for 循环里, 我们加上画测试图的部分. 注意在测试时, 要将网络改成 eval() 形式, 特别是 net_dropped, net_overfitting 改不改其实无所谓. 画好图再改回 train() 模式.
...
optimizer_ofit.step()
optimizer_drop.step()
# 接着上面来
if t % 10 == 0: # 每 10 步画一次图
# 将神经网络转换成测试形式, 画好图之后改回 训练形式
net_overfitting.eval()
net_dropped.eval() # 因为 drop 网络在 train 的时候和 test 的时候参数不一样.
...
test_pred_ofit = net_overfitting(test_x)
test_pred_drop = net_dropped(test_x)
...
# 将两个网络改回 训练形式
net_overfitting.train()
net_dropped.train()
import torch
import matplotlib.pyplot as plt
# torch.manual_seed(1) # reproducible
N_SAMPLES = 20
N_HIDDEN = 300
# training data
x = torch.unsqueeze(torch.linspace(-1, 1, N_SAMPLES), 1)
y = x + 0.3*torch.normal(torch.zeros(N_SAMPLES, 1), torch.ones(N_SAMPLES, 1))
# test data
test_x = torch.unsqueeze(torch.linspace(-1, 1, N_SAMPLES), 1)
test_y = test_x + 0.3*torch.normal(torch.zeros(N_SAMPLES, 1), torch.ones(N_SAMPLES, 1))
# show data
plt.scatter(x.data.numpy(), y.data.numpy(), c='magenta', s=50, alpha=0.5, label='train')
plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='cyan', s=50, alpha=0.5, label='test')
plt.legend(loc='upper left')
plt.ylim((-2.5, 2.5))
plt.show()
net_overfitting = torch.nn.Sequential(
torch.nn.Linear(1, N_HIDDEN),
torch.nn.ReLU(),
torch.nn.Linear(N_HIDDEN, N_HIDDEN),
torch.nn.ReLU(),
torch.nn.Linear(N_HIDDEN, 1),
)
net_dropped = torch.nn.Sequential(
torch.nn.Linear(1, N_HIDDEN),
torch.nn.Dropout(0.5), # drop 50% of the neuron
torch.nn.ReLU(),
torch.nn.Linear(N_HIDDEN, N_HIDDEN),
torch.nn.Dropout(0.5), # drop 50% of the neuron
torch.nn.ReLU(),
torch.nn.Linear(N_HIDDEN, 1),
)
print(net_overfitting) # net architecture
print(net_dropped)
optimizer_ofit = torch.optim.Adam(net_overfitting.parameters(), lr=0.01)
optimizer_drop = torch.optim.Adam(net_dropped.parameters(), lr=0.01)
loss_func = torch.nn.MSELoss()
plt.ion() # something about plotting
for t in range(500):
pred_ofit = net_overfitting(x)
pred_drop = net_dropped(x)
loss_ofit = loss_func(pred_ofit, y)
loss_drop = loss_func(pred_drop, y)
optimizer_ofit.zero_grad()
optimizer_drop.zero_grad()
loss_ofit.backward()
loss_drop.backward()
optimizer_ofit.step()
optimizer_drop.step()
if t % 10 == 0:
# change to eval mode in order to fix drop out effect
net_overfitting.eval()
net_dropped.eval() # parameters for dropout differ from train mode
# plotting
plt.cla()
test_pred_ofit = net_overfitting(test_x)
test_pred_drop = net_dropped(test_x)
plt.scatter(x.data.numpy(), y.data.numpy(), c='magenta', s=50, alpha=0.3, label='train')
plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='cyan', s=50, alpha=0.3, label='test')
plt.plot(test_x.data.numpy(), test_pred_ofit.data.numpy(), 'r-', lw=3, label='overfitting')
plt.plot(test_x.data.numpy(), test_pred_drop.data.numpy(), 'b--', lw=3, label='dropout(50%)')
plt.text(0, -1.2, 'overfitting loss=%.4f' % loss_func(test_pred_ofit, test_y).data.numpy(), fontdict={'size': 20, 'color': 'red'})
plt.text(0, -1.5, 'dropout loss=%.4f' % loss_func(test_pred_drop, test_y).data.numpy(), fontdict={'size': 20, 'color': 'blue'})
plt.legend(loc='upper left'); plt.ylim((-2.5, 2.5));plt.pause(0.1)
# change back to train mode
net_overfitting.train()
net_dropped.train()
plt.ioff()
plt.show()
Batch Normalization 批标准化
批标准化通俗来说就是对每一层神经网络进行标准化 (normalize) 处理, 我们知道对输入数据进行标准化能让机器学习有效率地学习.
1.做点数据
自己做一些伪数据, 用来模拟真实情况. 而且 Batch Normalization (之后都简称BN) 还能有效的控制坏的参数初始化 (initialization), 比如说 ReLU 这种激励函数最怕所有的值都落在附属区间, 那我们就将所有的参数都水平移动一个 -0.2 (bias_initialization = -0.2), 来看看 BN 的实力.
import torch
from torch import nn
from torch.nn import init
import torch.utils.data as Data
import torch.nn.functional as F
import matplotlib.pyplot as plt
import numpy as np
# 超参数
N_SAMPLES = 2000
BATCH_SIZE = 64
EPOCH = 12
LR = 0.03
N_HIDDEN = 8
ACTIVATION = F.tanh # 你可以换 relu 试试
B_INIT = -0.2 # 模拟不好的 参数初始化
# training data
x = np.linspace(-7, 10, N_SAMPLES)[:, np.newaxis]
noise = np.random.normal(0, 2, x.shape)
y = np.square(x) - 5 + noise
# test data
test_x = np.linspace(-7, 10, 200)[:, np.newaxis]
noise = np.random.normal(0, 2, test_x.shape)
test_y = np.square(test_x) - 5 + noise
train_x, train_y = torch.from_numpy(x).float(), torch.from_numpy(y).float()
test_x = torch.from_numpy(test_x).float()
test_y = torch.from_numpy(test_y).float()
train_dataset = Data.TensorDataset(train_x, train_y)
train_loader = Data.DataLoader(dataset=train_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=2,)
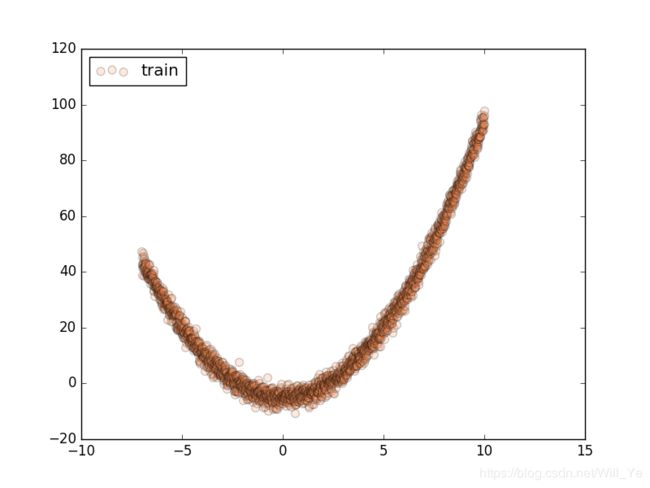
# show data
plt.scatter(train_x.numpy(), train_y.numpy(), c='#FF9359', s=50, alpha=0.2, label='train')
plt.legend(loc='upper left')
plt.show()
2.搭建神经网络
这里就教你如何构建带有 BN 的神经网络的. BN 其实可以看做是一个 layer (BN layer). 我们就像平时加层一样加 BN layer 就好了. 注意, 我还对输入数据进行了一个 BN 处理, 因为如果你把输入数据看出是 从前面一层来的输出数据, 我们同样也能对她进行 BN. 注意, 视频里面对于 momentum 的描述说错了, 不是用来更新缩减和平移参数的, 而是用来平滑化 batch mean and stddev 的
class Net(nn.Module):
def __init__(self, batch_normalization=False):
super(Net, self).__init__()
self.do_bn = batch_normalization
self.fcs = [] # 太多层了, 我们用 for loop 建立
self.bns = []
self.bn_input = nn.BatchNorm1d(1, momentum=0.5) # 给 input 的 BN
for i in range(N_HIDDEN): # 建层
input_size = 1 if i == 0 else 10
fc = nn.Linear(input_size, 10)
setattr(self, 'fc%i' % i, fc) # 注意! pytorch 一定要你将层信息变成 class 的属性! 我在这里花了2天时间发现了这个 bug
self._set_init(fc) # 参数初始化
self.fcs.append(fc)
if self.do_bn:
bn = nn.BatchNorm1d(10, momentum=0.5)
setattr(self, 'bn%i' % i, bn) # 注意! pytorch 一定要你将层信息变成 class 的属性! 我在这里花了2天时间发现了这个 bug
self.bns.append(bn)
self.predict = nn.Linear(10, 1) # output layer
self._set_init(self.predict) # 参数初始化
def _set_init(self, layer): # 参数初始化
init.normal_(layer.weight, mean=0., std=.1)
init.constant_(layer.bias, B_INIT)
def forward(self, x):
pre_activation = [x]
if self.do_bn: x = self.bn_input(x) # 判断是否要加 BN
layer_input = [x]
for i in range(N_HIDDEN):
x = self.fcs[i](x)
pre_activation.append(x) # 为之后出图
if self.do_bn: x = self.bns[i](x) # 判断是否要加 BN
x = ACTIVATION(x)
layer_input.append(x) # 为之后出图
out = self.predict(x)
return out, layer_input, pre_activation
# 建立两个 net, 一个有 BN, 一个没有
nets = [Net(batch_normalization=False), Net(batch_normalization=True)]
3.训练
训练的时候, 这两个神经网络分开训练. 训练的环境都一样.
opts = [torch.optim.Adam(net.parameters(), lr=LR) for net in nets]
loss_func = torch.nn.MSELoss()
losses = [[], []] # 每个网络一个 list 来记录误差
for epoch in range(EPOCH):
print('Epoch: ', epoch)
for step, (b_x, b_y) in enumerate(train_loader):
for net, opt in zip(nets, opts): # 训练两个网络
pred, _, _ = net(b_x)
loss = loss_func(pred, b_y)
opt.zero_grad()
loss.backward()
opt.step() # 这也会训练 BN 里面的参数
4.画图
这个教程有几张图要画, 首先我们画训练时的动态图. 我单独定义了一个画动图的功能 plot_histogram()
f, axs = plt.subplots(4, N_HIDDEN+1, figsize=(10, 5))
def plot_histogram(l_in, l_in_bn, pre_ac, pre_ac_bn):
...
for epoch in range(EPOCH):
layer_inputs, pre_acts = [], []
for net, l in zip(nets, losses):
# 一定要把 net 的设置成 eval 模式, eval下的 BN 参数会被固定
net.eval()
pred, layer_input, pre_act = net(test_x)
l.append(loss_func(pred, test_y).data[0])
layer_inputs.append(layer_input)
pre_acts.append(pre_act)
# 收集好信息后将 net 设置成 train 模式, 继续训练
net.train()
plot_histogram(*layer_inputs, *pre_acts) # plot histogram
# 后面接着之前 for loop 中的代码来
for step, (b_x, b_y) in enumerate(train_loader):
...
5.对比结果
首先来看看这次对比的两个激励函数是长什么样:
 然后我们来对比使用不同激励函数的结果.
然后我们来对比使用不同激励函数的结果.
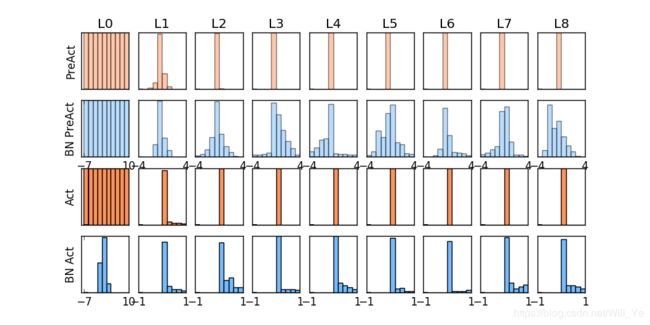

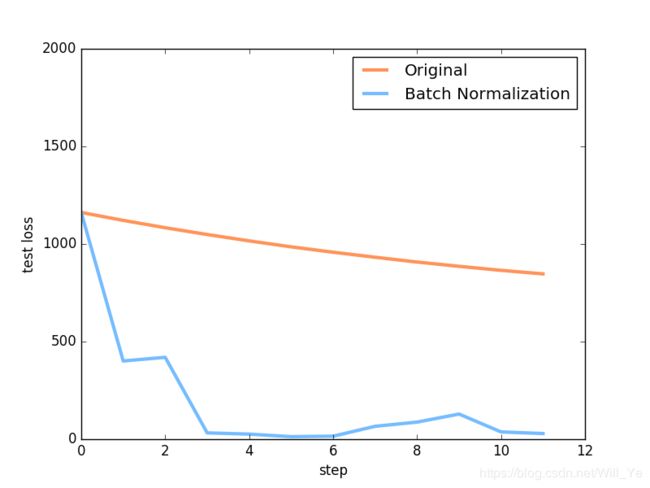 上面是使用
上面是使用 relu 激励函数的结果, 我们可以看到, 没有使用 BN 的误差要高, 线条不能拟合数据, 原因是我们有一个 “Bad initialization”, 初始 bias = -0.2, 这一招, 让 relu 无法捕捉到在负数区间的输入值. 而有了 BN, 这就不成问题了.


 上面结果是使用
上面结果是使用 tanh 作为激励函数的结果, 可以看出, 不好的初始化, 让输入数据在激活前分散得非常离散, 而有了 BN, 数据都被收拢了. 收拢的数据再放入激励函数就能很好地利用激励函数的非线性. 而且可以看出没有 BN 的数据让激活后的结果都分布在 tanh 的两端, 而这两端的梯度又非常的小, 是的后面的误差都不能往前传, 导致神经网络死掉了.
import torch
from torch import nn
from torch.nn import init
import torch.utils.data as Data
import matplotlib.pyplot as plt
import numpy as np
# torch.manual_seed(1) # reproducible
# np.random.seed(1)
# Hyper parameters
N_SAMPLES = 2000
BATCH_SIZE = 64
EPOCH = 12
LR = 0.03
N_HIDDEN = 8
ACTIVATION = torch.tanh
B_INIT = -0.2 # use a bad bias constant initializer
# training data
x = np.linspace(-7, 10, N_SAMPLES)[:, np.newaxis]
noise = np.random.normal(0, 2, x.shape)
y = np.square(x) - 5 + noise
# test data
test_x = np.linspace(-7, 10, 200)[:, np.newaxis]
noise = np.random.normal(0, 2, test_x.shape)
test_y = np.square(test_x) - 5 + noise
train_x, train_y = torch.from_numpy(x).float(), torch.from_numpy(y).float()
test_x = torch.from_numpy(test_x).float()
test_y = torch.from_numpy(test_y).float()
train_dataset = Data.TensorDataset(train_x, train_y)
train_loader = Data.DataLoader(dataset=train_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=2,)
# show data
plt.scatter(train_x.numpy(), train_y.numpy(), c='#FF9359', s=50, alpha=0.2, label='train')
plt.legend(loc='upper left')
class Net(nn.Module):
def __init__(self, batch_normalization=False):
super(Net, self).__init__()
self.do_bn = batch_normalization
self.fcs = []
self.bns = []
self.bn_input = nn.BatchNorm1d(1, momentum=0.5) # for input data
for i in range(N_HIDDEN): # build hidden layers and BN layers
input_size = 1 if i == 0 else 10
fc = nn.Linear(input_size, 10)
setattr(self, 'fc%i' % i, fc) # IMPORTANT set layer to the Module
self._set_init(fc) # parameters initialization
self.fcs.append(fc)
if self.do_bn:
bn = nn.BatchNorm1d(10, momentum=0.5)
setattr(self, 'bn%i' % i, bn) # IMPORTANT set layer to the Module
self.bns.append(bn)
self.predict = nn.Linear(10, 1) # output layer
self._set_init(self.predict) # parameters initialization
def _set_init(self, layer):
init.normal_(layer.weight, mean=0., std=.1)
init.constant_(layer.bias, B_INIT)
def forward(self, x):
pre_activation = [x]
if self.do_bn: x = self.bn_input(x) # input batch normalization
layer_input = [x]
for i in range(N_HIDDEN):
x = self.fcs[i](x)
pre_activation.append(x)
if self.do_bn: x = self.bns[i](x) # batch normalization
x = ACTIVATION(x)
layer_input.append(x)
out = self.predict(x)
return out, layer_input, pre_activation
nets = [Net(batch_normalization=False), Net(batch_normalization=True)]
# print(*nets) # print net architecture
opts = [torch.optim.Adam(net.parameters(), lr=LR) for net in nets]
loss_func = torch.nn.MSELoss()
def plot_histogram(l_in, l_in_bn, pre_ac, pre_ac_bn):
for i, (ax_pa, ax_pa_bn, ax, ax_bn) in enumerate(zip(axs[0, :], axs[1, :], axs[2, :], axs[3, :])):
[a.clear() for a in [ax_pa, ax_pa_bn, ax, ax_bn]]
if i == 0:
p_range = (-7, 10);the_range = (-7, 10)
else:
p_range = (-4, 4);the_range = (-1, 1)
ax_pa.set_title('L' + str(i))
ax_pa.hist(pre_ac[i].data.numpy().ravel(), bins=10, range=p_range, color='#FF9359', alpha=0.5);ax_pa_bn.hist(pre_ac_bn[i].data.numpy().ravel(), bins=10, range=p_range, color='#74BCFF', alpha=0.5)
ax.hist(l_in[i].data.numpy().ravel(), bins=10, range=the_range, color='#FF9359');ax_bn.hist(l_in_bn[i].data.numpy().ravel(), bins=10, range=the_range, color='#74BCFF')
for a in [ax_pa, ax, ax_pa_bn, ax_bn]: a.set_yticks(());a.set_xticks(())
ax_pa_bn.set_xticks(p_range);ax_bn.set_xticks(the_range)
axs[0, 0].set_ylabel('PreAct');axs[1, 0].set_ylabel('BN PreAct');axs[2, 0].set_ylabel('Act');axs[3, 0].set_ylabel('BN Act')
plt.pause(0.01)
if __name__ == "__main__":
f, axs = plt.subplots(4, N_HIDDEN + 1, figsize=(10, 5))
plt.ion() # something about plotting
plt.show()
# training
losses = [[], []] # recode loss for two networks
for epoch in range(EPOCH):
print('Epoch: ', epoch)
layer_inputs, pre_acts = [], []
for net, l in zip(nets, losses):
net.eval() # set eval mode to fix moving_mean and moving_var
pred, layer_input, pre_act = net(test_x)
l.append(loss_func(pred, test_y).data.item())
layer_inputs.append(layer_input)
pre_acts.append(pre_act)
net.train() # free moving_mean and moving_var
plot_histogram(*layer_inputs, *pre_acts) # plot histogram
for step, (b_x, b_y) in enumerate(train_loader):
for net, opt in zip(nets, opts): # train for each network
pred, _, _ = net(b_x)
loss = loss_func(pred, b_y)
opt.zero_grad()
loss.backward()
opt.step() # it will also learns the parameters in Batch Normalization
plt.ioff()
# plot training loss
plt.figure(2)
plt.plot(losses[0], c='#FF9359', lw=3, label='Original')
plt.plot(losses[1], c='#74BCFF', lw=3, label='Batch Normalization')
plt.xlabel('step');plt.ylabel('test loss');plt.ylim((0, 2000));plt.legend(loc='best')
# evaluation
# set net to eval mode to freeze the parameters in batch normalization layers
[net.eval() for net in nets] # set eval mode to fix moving_mean and moving_var
preds = [net(test_x)[0] for net in nets]
plt.figure(3)
plt.plot(test_x.data.numpy(), preds[0].data.numpy(), c='#FF9359', lw=4, label='Original')
plt.plot(test_x.data.numpy(), preds[1].data.numpy(), c='#74BCFF', lw=4, label='Batch Normalization')
plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='r', s=50, alpha=0.2, label='train')
plt.legend(loc='best')
plt.show()