0基础学图论!——图论精讲/详细/新手理解概念必看!
并不会有更好的阅读体验
特别特别感谢:
l m p p lmpp lmpp大佬牺牲自己宝贵时间,为我没有脾气的耐心讲解。
B e y o n d H e a v e n BeyondHeaven BeyondHeaven大佬,无偿帮我康博客,甚至和我这个陌生的蒟蒻分享自己的故事,带给了我知识和温暖。真的、真的非常谢谢宁! q w q qwq qwq
F l y Fly Fly_ F u n n y Funny Funny大佬,理会了一个无关紧要的人的丧气话,并且带给了她把这篇博文更完的动力。
真的很感谢我的教练 d i d did did,他的宽容友爱和超一流的教学水准不仅让我迈上了 O I OI OI的正轨,更让我感受到了朋友的温暖。
还有很多很多好朋友帮助了我(详见友链),真的非常感谢你们!
没有你们就没有这篇博客,我也会比现在蒻上 i n f inf inf倍。
提示:
本博客还并没有做到完全是自己总结的概念,但是我已经正在努力填坑了 Q A Q QAQ QAQ。
本文将以尽量朴(全)实(口)无(水)华(话)的语言和自己的一些奇奇怪怪的想法,为您呈现一个我眼中的图论世界。
在我自己掌握特别不好的题目/知识点旁会加以 ! \color{Red}\colorbox{Yellow}{!} ! 的标记。
所有题号以 B S O J BSOJ BSOJ为准。所有题目已经附上了题干和样例数据。题目链接我也正在尽量引用公开的大 O J OJ OJ上的题目,方便大家做题学习。注意!有些题的代码可能和附上的链接题目不能吻合,但题目的思路一定都是一致的,只是细节上的不同,具体代码对应的题干还是看我附在代码前的题干!
有什么错误纰漏的直接 Q Q QQ QQ+洛谷私信+讨论区留言,我真的超级需要您的反馈的 q w q qwq qwq。
希望能您能从这份清单中找到您的一些知识漏洞并把它们补起来!
更新信息
2020.3.29 2020.3.29 2020.3.29 1.0 1.0 1.0版本,开始新的篇章。知识点记录至拓扑排序模板题。
2020.3.30 2020.3.30 2020.3.30 && 2020.3.31 2020.3.31 2020.3.31 2.0 2.0 2.0版本,爆肝完所有知识点。
2020.5.6 2020.5.6 2020.5.6 2.5.0 2.5.0 2.5.0版本,在自己的反复体会和阅读学习后进行了对文本效果、知识内容方面修复部分问题。拓扑排序部分已删去死板概念,换为自己理解。
2020.5.7 2020.5.7 2020.5.7 2.5.1 2.5.1 2.5.1版本,书面上已经总结完了 K r u s k a l Kruskal Kruskal算法,博客上还没整完。
2020.5.8 2020.5.8 2020.5.8 2.5.2 2.5.2 2.5.2版本,书面上已经总结完了 P r i m Prim Prim算法,博客上还没整完。
2020.5.10 2020.5.10 2020.5.10 2.5.3 2.5.3 2.5.3版本,书面上已经总结完了 F l o y d Floyd Floyd算法,博客上还没整完。(发现一直以来 F l o y d Floyd Floyd大神的名字都写错了,真的对不起了呜呜呜呜)
2020.5.11 2020.5.11 2020.5.11 2.5.4 2.5.4 2.5.4版本,书面上已总结了一丢丢 S P F A SPFA SPFA,未完待续。
2020.5.12 2020.5.12 2020.5.12 2.5.4.5 2.5.4.5 2.5.4.5版本,乌龟速度更进 S P F A SPFA SPFA,废话一堆堆,未(我)完(想)待(烂)续(尾)。
2020.6.8 2020.6.8 2020.6.8 2.5.5 2.5.5 2.5.5版本,把之前的数字和字母做了优化, T a r j a n Tarjan Tarjan开始更新。不要问我为什么拖了这么久才又开始更。别问,问就是半期考试。不要问我半期考得怎么样。别问,问就是全班垫底(bushi)
2020.6.9 2020.6.9 2020.6.9 2.5.6 2.5.6 2.5.6版本,书面上已经总结完了 T a r j a n Tarjan Tarjan的基本概念,开始更新割点之类的概念。总结上 T a r j a n Tarjan Tarjan还没更完,发给了 d i d did did康康,我怀疑他不会回我。
2020.7.11 2020.7.11 2020.7.11 2.6.0 2.6.0 2.6.0版本,直接到 2.6 2.6 2.6版本是因为之前陆陆续续有在做一些修改和删减,大概可以算是 2.6.0 2.6.0 2.6.0版本了叭?……(小声)
2020.7.12 2020.7.12 2020.7.12 2.6.0 2.6.0 2.6.0版本,准备放弃了,大概是和 O I OI OI没有缘分了。在 l u o g u luogu luogu上发表了一篇丧丧的文章吧,应该没有人会理我的,希望负能量没有影响到大家 o r z orz orz
2020.7.14 2020.7.14 2020.7.14 2.6.0.1 2.6.0.1 2.6.0.1版本,在 l u o g u luogu luogu上丧气的文章, t a o x u a n y u taoxuanyu taoxuanyu大佬鼓励了我,挺好,所以还是决定在这篇文章不要烂尾,至少题目的链接啊,题干啥的还是要放一放,知识点看了一下,应该也是没有问题的。想了想还是给丧气话加上了渲染(((算是在 O I OI OI留下自己一个完整的脚印吧。
备忘录- T O TO TO D O DO DO L i s t List List
-
把原题目链接换成大 O J OJ OJ的题目链接 -
附上题目的题干和样例数据 -
(缓慢任务)删掉一些毫无营养的口水话,但是不能影响详细、搞笑(?)的风格
拓扑排序:
什么是拓扑排序?
拓扑排序,通过名字里的“排序”,我们自然知道了它的功能——排序。
那么,它怎样排序的?又是为谁排序的?
拓扑排序的简单规则
“排序”,一个多么简单的概念。在你的脑海里,“排序”是否具有以下特征呢?
- 一堆数据
- 一些规则
正如大多数排序一样,拓扑排序也具有以上的简单特征。
从“一堆数据”开始思考
不妨想想,作为一个图工作的排序,怎样才能构造出“一堆”数据呢?
答案是明显的,我们应该将图中的每一个节点取出,形成我们排序所需的一堆数据。
可是我们怎么选择取出的节点呢?真就毫无目标 r a n d ( ) rand() rand()函数随机整一个?
如果想到了这点,我们就可以开始考虑拓扑排序的规则。
怎样用“一些规则”排序?
所谓规则,就是一个算法进行操作的方法。
对于拓扑排序来说,它的操作方法便是如下 3 3 3步:
- 寻找一个入度为 0 0 0的点(为什么?
这就是“规则”,定死了的,不然你咋不问我为啥1+1=2人为规定的,不然怎么开始排序???) - 取出这个点,随之被删除的还有和这个点所有直接相连的边
- 在剩下的节点中重复第 1 1 1、 2 2 2步,直至所有节点被取出
我们对谁使用拓扑排序?/ 谁身上才能使用拓扑排序?
我们对 D A G DAG DAG——即:有向无环图使用拓扑排序。
为什么我们只能对 D A G DAG DAG进行拓扑排序?
通过刚刚的过程分析,我们可以轻易地发现一个问题:如果当前的节点没有全部被取出,但却已经发现不了入度为 0 0 0的节点,那么我们就不能愉快的继续拓扑排序了。
不妨思考一下为什么会出现这种 b u g bug bug。
一切的证据都指向有向有环图。(无向就不说了,咋整都是个环)
为啥?我们先来看看下图——一个有向有环图,来模拟一下拓扑排序的过程:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jky5eqRY-1594772179294)(https://mrcontinue.github.io/post-images/1588862342176.png)]
第一步,我们找出了入度为 0 0 0的节点①,并且将它和它相关联的边取出。
于是乎,现在的图是这样的:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nefSZH5I-1594772179295)(https://mrcontinue.github.io/post-images/1588862416195.png)]
这时我们可以发现一个有趣的事情。由于②、③。④三个点形成了一个环,所以现在图中没有入度为 0 0 0的点。
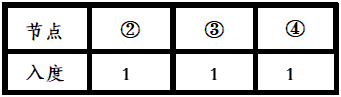
所以此时就会出现无法继续进行拓扑排序的问题。而这一切正是印证了拓扑排序只能在 D A G DAG DAG图里进行操作的事实。
关于拓扑排序的应用
拓扑排序一般很少有单独针对该知识点的题,但是在关键路径和平常的其他例题的辅助操作中却发挥着重要作用。所以掌握好拓扑排序是很重要的事情。
1462 1462 1462 拓扑排序(这题实在太水了,大 O J OJ OJ上根本找不到,只好把题干和样例附在这里,提交就随缘吧((()
D e s c r i p t i o n Description Description
对一个有向图(Directed Acyclic Graph简称DAG) G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若 ∈E(G),则u在线性序列中出现在v之前。
若图中存在有向环,则不可能使顶点满足拓扑次序。
I n p u t Input Input
第1行:2个空格分开的整数n和m,分别表示图的顶点数和边数。
第2..m+1行:每行2个空格分开的整数i,j,i表示一条边的起点,j表示终点。
O u t p u t Output Output
拓扑序,顶点从1开始编号,如果有多个拓扑序,则顶点编号小的优先输出。
有环输出:no solution
S a m p l e Sample Sample I n p u t Input Input
【样例输入1】
4 4
1 3
1 4
2 3
2 4
【样例输入2】
4 4
1 2
2 3
3 4
4 1
S a m p l e Sample Sample O u t p u t Output Output
【样例输出1】
1 2 3 4
【样例输出2】
no solution
H i n t Hint Hint
【数据范围】
1≤n≤200
1≤m≤20000
本代码按字典序输出的部分:
int j=1; //从第一个点开始查找
while(j<=n&&bein[j])
j++; //统计入度为零的节点
//由于-1的bool值也视作真,所以可以标记为-1
if(j>n) return 0; //如果统计的节点超出了范围n,说明这个图有环
sum[++top]=j; //拓扑序列答案数组统计新答案
//本代码由邻接矩阵实现,按字典序输出,复杂度O(n^2)
#include 最小生成树(英文缩写 M S T MST MST我忘了全称叫啥了反正知道了也没啥用)
-
最小生成树:在一张带权的无向连通图中,各边权和为最小的一颗生成树即为最小生成树。
简单讲:找出连接所有点的最低成本路线。
举个栗子,下面这个图中的最小生成树就是用红线标出的:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-E61AGA65-1594772179300)(https://mrcontinue.github.io/post-images/1588863097566.png)] -
最小边原则:图中权值最小的边(如果唯一的话)一定在MST上。
为啥?试想,既然 M S T MST MST的路径一定会连接至每个节点,那么我们一定会尽量选择最小的边以到达目标节点。(不然合着有最短的路不走走绕路??)
K r u s k a l Kruskal Kruskal算法
K r u d k a l Krudkal Krudkal算法的基本知识
K r u s k a l Kruskal Kruskal算法是一种贪心算法。为什么是贪心?知道了过程你就知道了。
K r u s k a l Kruskal Kruskal的操作方法:
- 按图中的边按权值从小到大快排(为啥?详见楼上【最小边原则】,您品,您细品)。
- 按照权值从小到大依次选边,若当前选取的边加入后使生成树形成环,则舍弃当前边(原因后面会讲的);否则标记当前边已遍历并计数。
- 重复2的操作,直到生成树中包含 ( n − 1 ) (n-1) (n−1)条边为止;否则当遍历完所有的边后,都不能选取 ( n − 1 ) (n-1) (n−1)条边,表示最小生成树不存在。
从上面 K r u s k a l Kruskal Kruskal直接快排再无脑选边,当前不符合条件就直接舍弃,完全不考虑未来的步骤中,可以隐(强)约(烈)地感受到“鼠目寸光”的贪心内味。(有内味了. j p g jpg jpg)
接下来咱简要的抠一抠算法里的细节。
怎么判断当前边加入后, M S T MST MST会不会形成环?
我们先来欣赏一个美丽的环,请您尽量把它想象成一棵变异了的二叉树——因为它有环:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OTXGZ2Fw-1594772179301)(https://mrcontinue.github.io/post-images/1588864164761.png)]
可以看见,这棵奇怪的树分外耀眼的 p o i n t point point是节点4同时拥有了两个父亲——即节点 2 2 2和节点 3 3 3。
如果它与任意一个父亲断掉连接,那么它还是一棵健康茁壮的二叉树:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dMpdmpXV-1594772179302)(https://mrcontinue.github.io/post-images/1588948569959.png)]
所以我们可以推出,判断一棵树上有没有环,可以直接检查一个儿子是否拥有多个父亲。放在无向图里,我们可以变相理解为:多个节点是否同时联向同一个节点,即,有没有多个节点属于同一个集合。
欸?集合?判断?
有没有很熟悉的感觉?(别告诉我你没有,你就是有(大雾))
没错,你想起了并查集!就是那个可以储存所属集合、可以直接合并两个集合的神奇数据结构。
H o w e v e r How ever However,我们就是用并查集来储存所有的节点,也正好利用它的特性——可以非常简单的判断所属集合,这点,来判断新加入的节点是否会让 M S T MST MST产生环。
并查集的基本操作:
1. 1. 1. 找根节点:
int GetFather(int x)
{
if(prt[x]==x) return x;
return prt[x]=GetFather(prt[x]); //路径压缩
}
2. 2. 2. 合并操作(一般可以直接写在主函数里):
void Add(int x,int y)
{
int f1=GetFather(x);
int f2=GetFather(y);
if(f1!=f2) prt[f1]=f2;
}
1449 1449 1449 最小生成树
D e s c r i p t i o n Description Description
如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出 orz。
I n p u t Input Input
第一行包含两个整数N,M,表示该图共有N个结点和M条无向边。
接下来M行每行包含三个整数Xi,Yi,Zi,表示有一条长度为Zi的无向边连接结点 Xi,Yi。
O u t p u t Output Output
如果该图连通,则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出 orz。
S a m p l e I n p u t Sample Input SampleInput
4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3
S a m p l e O u t p u t Sample Output SampleOutput
7
H i n t Hint Hint
对于20%的数据,N≤5,M≤20。
对于40%的数据,N≤50,M≤2500。
对于70%的数据,N≤500,M≤2×10^5。
对于100%的数据,1≤N≤5000,1≤M≤2×10^5。
样例解释:
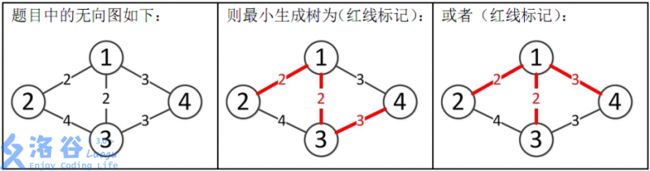
所以最小生成树的总边权为 2 + 2 + 3 = 7 2+2+3=7 2+2+3=7。
#include P r i m Prim Prim算法
为啥有了 K r u s k a l Kruskal Kruskal算法还要学 P r i m Prim Prim呢?
因为两种算法可以用于两种不同类型的图:稠密图和稀疏图。多一种方法多一种思路嘛 q w q qwq qwq。
P r i m Prim Prim算法的操作方法:
1. 1. 1. 将根节点插入集合 S S S中。
2. 2. 2. 在所有与 S S S集合的点相连的边中,找出一条最小的边,将这条边相连的另一个点——即未遍历的点,加入到集合 S S S中。
3. 3. 3. 重复步骤 2 2 2,直到所有节点都在 S S S中。
简单来说,就是 S S S集合中的元素从一个根节点 1 1 1开始,以一个集合整体出动的方式来扩展其他的点,以获取最小生成树。
用一个例子来表现一下上述内容,也许您会理解得更透彻。
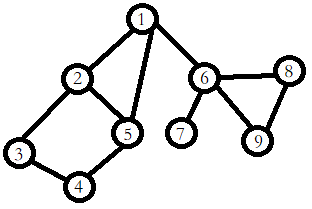
有一张图如下:
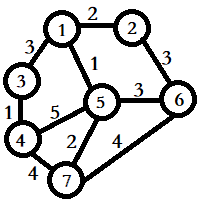
首先,我们将数组初始化为最大,即 i n f inf inf,以表示此时每个节点与集合毫不相干,随后,我们将源点 1 1 1号放入集合中。由于源点本身与本身的距离为 0 0 0,所以数组更新为 0 0 0:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5gMzoKC8-1594772179305)(https://mrcontinue.github.io/post-images/1589117587248.png)]
录入当前与整个集合距离最小的节点 5 5 5,将 d [ 5 ] d[5] d[5]更新为 1 1 1。集合拓展为①、⑤:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PjzpdwPj-1594772179306)(https://mrcontinue.github.io/post-images/1589117665395.png)]
将与当前集合距离最近的节点 7 7 7放入集合中:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-R7Ra41ok-1594772179307)(https://mrcontinue.github.io/post-images/1589117689666.png)]
接着放入节点 2 2 2,更新数组:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SggenaW9-1594772179308)(https://mrcontinue.github.io/post-images/1589117711223.png)]
此时可以发现,节点所连的点中出现了多个最小边权,即与①相连的③边权为 3 3 3;与②相连的⑥边权为 3 3 3;与⑤相连的⑥边权为 3 3 3。由于我们现在是举例,所以随便选择一个即可。真正代码里是根据被循环到的先后次序来决定的。
这里拓展了③并更新数组:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KXEJOSJP-1594772179309)(https://mrcontinue.github.io/post-images/1589117788916.png)]
拓展④并更新数组:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dUoZS8HZ-1594772179310)(https://mrcontinue.github.io/post-images/1589117813649.png)]
最后拓展完节点 6 6 6。而 M S T MST MST的总值在应该是程序中一边遍历一边累加的:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YcNXD5ii-1594772179311)(https://mrcontinue.github.io/post-images/1589117854832.png)]
模板题和代码深入理解
1449 1449 1449 最小生成树
D e s c r i p t i o n Description Description
如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出 orz。
I n p u t Input Input
第一行包含两个整数N,M,表示该图共有N个结点和M条无向边。
接下来M行每行包含三个整数Xi,Yi,Zi,表示有一条长度为Zi的无向边连接结点 Xi,Yi。
O u t p u t Output Output
如果该图连通,则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出 orz。
S a m p l e Sample Sample I n p u t Input Input
4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3
S a m p l e Sample Sample O u t p u t Output Output
7
H i n t Hint Hint
对于20%的数据,N≤5,M≤20。
对于40%的数据,N≤50,M≤2500。
对于70%的数据,N≤500,M≤2×10^5。
对于100%的数据,1≤N≤5000,1≤M≤2×10^5。
样例解释:

所以最小生成树的总边权为 2 + 2 + 3 = 7 2+2+3=7 2+2+3=7。
#include 最短路径问题
-
最短路径:在一个有权图中连接给定两个顶点的权值和最小的路径。
-
最短路树和最小生成树可以不一样。
-
一般有两类最短路问题:
- S S S P SSSP SSSP(单源最短路):求给定起点 S S S到其他所有点的最短路,常见算法有 D i j k s t r a Dijkstra Dijkstra算法、 S P F A SPFA SPFA算法等。
- A P S P APSP APSP(多源最短路):求任意两对顶点之间的最短路,常见算法有 F l o y e d Floyed Floyed算法。
单讲概念有点生涩,上一个例子理解一下:
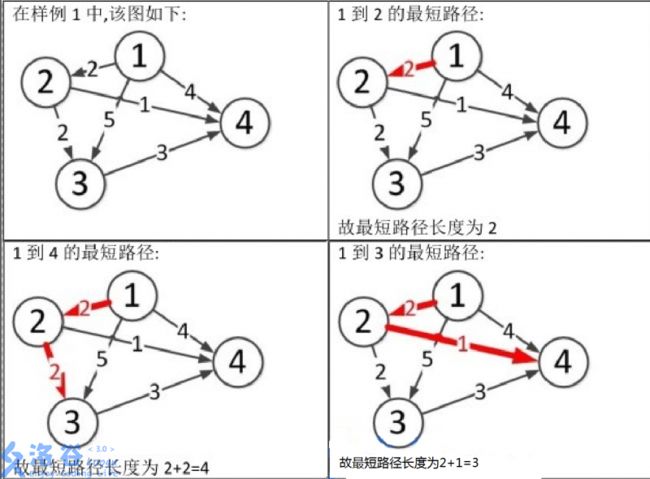
在下图中:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WWqle6tV-1594772179313)(https://mrcontinue.github.io/post-images/1589118649290.png)]
S S S P SSSP SSSP:只求①到⑤的最短路这一条最短路的值,即起点到终点的最短路。
A P S P APSP APSP:求①到③的最短路、②到④的最短路、①到⑤的最短路……即任意两点之间的最短路。
D i j k s t r a Dijkstra Dijkstra算法
三角形性质:
设源点 S S S到点 x x x、 y y y的最短路径长度为 d [ x ] d[x] d[x]、 d [ y ] d[y] d[y]。 x x x与 y y y之间的距离是 g [ x ] [ y ] g[x][y] g[x][y],则有下面的“三角形定理”:
d [ x ] + g [ x ] [ y ] > = d [ y ] d[x]+g[x][y]>=d[y] d[x]+g[x][y]>=d[y]
这段话是什么意思?
首先给定两个点 x x x、 y y y和它们的距离 g [ x ] [ y ] g[x][y] g[x][y]:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4gwkvC9r-1594772179314)(https://mrcontinue.github.io/post-images/1589119940828.png)]
接着我们向上拓展出一个与 x x x、 y y y相连的节点 S S S,其最短距离为 d [ x ] d[x] d[x]、 d [ y ] d[y] d[y]。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GqKGjrTJ-1594772179315)(https://mrcontinue.github.io/post-images/1589120116971.png)]
求解最短路的时候需要满足: d [ x ] + g [ x ] [ y ] > = d [ y ] d[x]+g[x][y]>=d[y] d[x]+g[x][y]>=d[y]
松弛:
若在处理过程中,有两点 x x x、 y y y出现不符合“三角形定理”,则可“松弛一下”,即:
if(d[x]+g[x][y]
D i j k s t r a Dijkstra Dijkstra算法的操作方法:
设根节点为 v 0 v0 v0,数组 d [ i ] d[i] d[i]表示 i i i到根节点的最短距离。
-
初始化 d [ v 0 ] = 0 d[v0]=0 d[v0]=0, v 0 v0 v0到其他点的距离值 d [ i ] = i n f d[i]=inf d[i]=inf。
-
经过 n n n次如下步骤操作,最后得到 v 0 v0 v0到 n n n个顶点的最短距离:
- 选择一个未标记(即未遍历过)的点 k k k并且 d [ k ] d[k] d[k]的值是当前最小的(之所以选当前最小的点开始继续连点是因为,最小的点可以有期望让到其他的点的边权尽量小)。
- 标记点 k k k已遍历,即 v i s [ k ] = 1 vis[k]=1 vis[k]=1。
- 以 k k k为中间点,修改源点 v 0 v0 v0到其他未标记点 j j j的距离值 d [ j ] d[j] d[j](即,又以 k k k为媒介,继续遍历其他与 k k k相连但没有被遍历的点,到源点的新距离)。
个人小议 D i j k s t r a Dijkstra Dijkstra算法与 P r i m Prim Prim算法的不同:
-
目的上, P r i m Prim Prim求最小生成树, D i j k s t r a Dijkstra Dijkstra求最短路
-
距离上, P r i m Prim Prim是让在集合里的所有点中,找到与之相连的一条最短边。
D i j k s t r a Dijkstra Dijkstra是从原点开始更新距离,然后点连点更新距离; -
连点上, P r i m Prim Prim是一个集合连所有点
D i j k s t r a Dijkstra Dijkstra是一个点只能连直接与自己相关联的点,在开始连接新的点的时候,从最小的点开始继续访问 -
P r i m Prim Prim算法数组里存的是点到集合的距离
D i j k s t r a Dijkstra Dijkstra算法数组里存的是所有点到源点的距离
总的来说, P r i m Prim Prim与 D i j k s t r a Dijkstra Dijkstra有很多相似之处,但有很多细节还是不同的,还是要注意区分和理解。
模板题和代码深入理解
1428 1428 1428 最短路径问题
D e s c r i p t i o n Description Description
平面上有n个点(n<=100),每个点的坐标均在-10000~10000之间。其中的一些点之间有连线。
若有连线,则表示可从一个点到达另一个点,即两点间有通路,通路的距离为两点间的直线距离。现在的任务是找出从一点到另一点之间的最短路径。
I n p u t Input Input
共n+m+3行,其中:
第一行为整数n。
第2行到第n+1行(共n行) ,每行两个整数x和y,描述了一个点的坐标。
第n+2行为一个整数m,表示图中连线的个数。
此后的m 行,每行描述一条连线,由两个整数i和j组成,表示第i个点和第j个点之间有连线。
最后一行:两个整数s和t,分别表示源点和目标点。
O u t p u t Output Output
一行,一个实数(保留两位小数),表示从s到t的最短路径长度。
S a m p l e Sample Sample I n p u t Input Input
5
0 0
2 0
2 2
0 2
3 1
5
1 2
1 3
1 4
2 5
3 5
1 5
S a m p l e Sample Sample O u t p u t Output Output
3.41
#include 寻找优化的办法(选读内容)
我们可以发现 D i j k s t r a Dijkstra Dijkstra是一个很好理解的算法,但是当节点一多,它较高的复杂度就显得有些力不从心了。所以我们试图寻找一种方法,使得它的复杂度能降到我们满意的程度。
那么我们简单分析一下 D i j k s t r a Dijkstra Dijkstra算法的大概步骤:
- 初始化
- 找当前集合内最小边权
- 更新每个节点新的边权值
在这三步里,初始化这一步很明显无法优化;而更新节点一定是要落实到每个节点的,所以循环一次的复杂度也是在做难免的。
那么我们的目光很确定的指向了【找当前集合内最小边权】这一步的优化方式。
还记得我们曾经学过的数据结构堆吗?它可以用一个 S T L STL STL库 p r i o r i t y priority priority_ q u e u e queue queue来实现。它插入元素的复杂度为 O ( n l o g n ) O(nlogn) O(nlogn),而查找元素的复杂度仅为 O ( 1 ) O(1) O(1)。所以我们大可利用它可以排序、查找复杂度低的特点对【找当前集合内最小边权】进行优化。
说详细一点,就是用一个结构体,将当前节点序号和它到源点的距离封装起来,再建立一个结构体优先队列进行操作。由于堆会维护自身的大小,所以取出时可以到达和原来一个循环做到的一个效果。
至于结构体优先队列的具体操作、优化版 D i j k s t r a Dijkstra Dijkstra的具体代码操作和例题详解,可移步至这里以获取更详细的知识。
F l o y d Floyd Floyd算法
F l o y d Floyd Floyd算法的基本知识:
- F l o y d Floyd Floyd算法是 D P DP DP思想。
- F l o y d Floyd Floyd算法可以处理有向图或无向图,但图中不能有负环。
F l o y d Floyd Floyd算法的基本思想:
-
初始化 f [ i ] [ j ] = w [ i ] [ j ] f[i][j]=w[i][j] f[i][j]=w[i][j],从小到大枚举 k k k,对每对节点 ( u , v ) (u,v) (u,v),检查它们的最短路值。
-
f [ i ] [ j ] f[i][j] f[i][j]表示该状态下(即路径中间只允许经过节点 i i i~ k k k的情况下, k k k递增,定义在循环内), i i i到 j j j的最短路距离
其状态转移方程分为两种情况进行 D P DP DP:- 最短路经过点k: f [ i ] [ j ] = f [ i ] [ k ] + f [ k ] [ j ] ; f[i][j]=f[i][k]+f[k][j]; f[i][j]=f[i][k]+f[k][j];
- 最短路不经过点k: f [ i ] [ j ] = f [ i ] [ j ] f[i][j]=f[i][j] f[i][j]=f[i][j](这里等号右边的 f [ i ] [ j ] f[i][j] f[i][j]实为上一阶段的 f [ i ] [ j ] f[i][j] f[i][j])
状态转移方程简单分析
其实这是一个一眼就能看出来的概念,这里在将图画出来,更便于大家理解,看看自己当初的理解是否有误。
- 两点之间有其它点。
如图:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kAewehVn-1594772179316)(https://mrcontinue.github.io/post-images/1589206151924.png)]
能一眼看出 f [ i ] [ j ] = f [ i ] [ k ] + f [ k ] [ j ] f[i][j]=f[i][k]+f[k][j] f[i][j]=f[i][k]+f[k][j]。 - 两点之间并没有任何的其他点,直接相连。
如图:
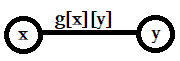
1584 1584 1584 银行设置
(没有找到大 O J OJ OJ的题目链接各位大佬还是将就着题干看吧,提交还是随缘吧((()
D e s c r i p t i o n Description Description
经过几十年的奋斗,X童鞋终于学出头了,他当了老板!有了钱的X童鞋回到了他亲爱的家乡,他发现,家乡的筒子们因为生在山卡卡里,所以十分跟不上潮流,借钱都要用鸡抵押,存钱都要塞在床底下。X童鞋觉得这很不科学,决定在他的家乡设置银行。但是,由于这个村里的筒子都太懒了,不肯多走几步,所以,X童鞋准备在n个居民点v1,v2,…,vn中设置两个很科学的银行,使每个村民都能懒到神一般的级别,所有人到银行的最短距离之和最小。然而,X童鞋也十分懒,所以,这个任务就交给勤奋的你们了O(∩_∩)O~
I n p u t Input Input
第一行有两个正整数N,M,分别表示居民点数和路的条数(N<=100,M<=10000)。
接下来M行,每行三个正整数,分别表示每一条路的两个端点编号和长度。
O u t p u t Output Output
输出两个银行分别设置在什么地方,如果有多个解,输出编号最小的两个
S a m p l e Sample Sample I n p u t Input Input
3 3
1 2 1
2 3 2
1 3 2
S a m p l e Sample Sample O u t p u t Output Output
1 3
初始化:
{ f [ i ] [ j ] = 0 i = = j ( 自 己 到 自 己 的 距 离 为 0 ) f [ i ] [ j ] = i n f i ! = j ( 初 始 设 置 为 两 节 点 毫 无 关 联 , 即 距 离 上 等 于 i n f ) \begin{cases}f[i][j]=0&i==j(自己到自己的距离为0)\\f[i][j]=inf&i!=j(初始设置为两节点毫无关联,即距离上等于inf)\end{cases} {f[i][j]=0f[i][j]=infi==j(自己到自己的距离为0)i!=j(初始设置为两节点毫无关联,即距离上等于inf)
#include S P F A SPFA SPFA算法
S P F A SPFA SPFA算法的基本思想和操作方法
-
用一个队列储存待优化的节点(注意,这里队列里储存的是节点,而堆优化 D i j Dij Dij的优先队列里则储存的是从这个节点和它对应的到源点的最短路径的距离,我们可以近似的看成一条“路径”。这里由于我曾经迷惑过一段时间,所以特此提示)
-
每次优化是取出队首元素 x x x,遍历每个和 x x x相关的节点 y y y,看 y y y是否需要进行松弛操作。如果 y y y进行了松弛操作,即它更新了自己到源点的距离,则将它放入队列中。
-
反复循环,直至队列为空。
常见疑惑:
-
Q Q Q: S P F A SPFA SPFA算法的复杂度?
A A A:玄学,平均复杂度为 O ( 2 E ) O(2E) O(2E),其大时可以极大,小时可以极小所以才说SPFA它死了啊。 -
Q Q Q:在算法中,如果后出队的点可以使前面的点更忧,而那个点的值改变了,它的子节点的值也会改变。这个时候需要入队吗?
A A A:需要,而且不用担心 v i s [ i ] = 1 vis[i]=1 vis[i]=1的问题。当我们出队以后 v i s [ i ] vis[i] vis[i]会归零的。
1580 1580 1580 最短路 ( S p f a ) 2885 (Spfa)2885 (Spfa)2885
D e s c r i p t i o n Description Description
本题测试数据为随机数据,在考试中可能会出现构造数据让SPFA不通过,如有需要请移步P4779。
I n p u t Input Input
第一行包含三个整数n,m,s分别表示点的个数、有向边的个数、出发点的编号。
接下来m行每行包含三个整数u,v,w表示一条u→v的,长度为w的边。
O u t p u t Output Output
输出一行n个整数,第i个表示s到第i个点的最短路径,若不能到达则输出 2^{31}−1
S a m p l e Sample Sample I n p u t Input Input
4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4
S a m p l e Sample Sample O u t p u t Output Output
0 2 4 3
H i n t Hint Hint
【数据范围】
对于20%的数据:1≤n≤5,1≤m≤15;
对于40%的数据:1≤n≤100,1≤m≤10^4;
对于70%的数据:1≤n≤1000,1≤m≤10^5;
对于100%的数据:1≤n≤10^4,1≤m≤5×10^5,保证数据随机。
对于真正100%的数据,请移步P4779。请注意,该题与本题数据范围略有不同。
图片1到3和1到4的文字位置调换。
#include
Spfa(1);
cout<<d[n]<<endl; //直接输出
return 0;
}
! \color{Red}\colorbox{Yellow}{!} !
有向图的连通性
关于有向图的相关概念:
-
父子边: A A A是 B B B的父亲,边 A B AB AB可理解为一条父子边。
-
返祖边: A A A是 B B B的父亲, B B B是 C C C的父亲,边 A C AC AC可理解为一条返祖边。
-
横叉边: A A A是 B B B的父亲, A A A是 C C C的父亲,边 B C BC BC可理解为一条横叉边。
-
强连通图:有向图中,如果对每一对 V i Vi Vi, V j Vj Vj( V i Vi Vi, V j Vj Vj属于 V V V, V i Vi Vi不等于 V j Vj Vj)。从 V i Vi Vi到 V j Vj Vj和从 V j Vj Vj到 V i Vi Vi都存在路径,则称 G G G是强连通图。
简单来说,即:如果一张有向图中任意两点有路径可以互相到达,则称这张图是强连通图 -
强连通分量:有向图的极大强连通子图叫强连通分量。
T a r j a n Tarjan Tarjan算法
T a r j a n Tarjan Tarjan算法可以用来干什么?
-
求出有向图的强连通分量,无向图的双连通分量(后面会讲的)
-
在线性的时间内求出无向图的割点和桥(后面会讲的)
T a r j a n Tarjan Tarjan算法的基本知识(部分思路来源于《算法竞赛进阶指南》)
从一张没有灵魂的图说起
这里有一张没有灵魂的无向图:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UBeUlCYG-1594772179318)(https://mrcontinue.github.io/post-images/1591708226129.png)]
可以发现它没有灵魂的原因在于它没有每个节点的编号(极其牵强的理由)。
所以我们应该怎么为节点们编号呢?
……
时间戳( D F N DFN DFN,我们有时会叫它“豆腐脑”,DouFuNao嘛)
有啦! D F S DFS DFS是一个非常棒的东西,用它的遍历次序来编号,即不会重,又不会漏。
所以我们可以将 D F S DFS DFS第一次遍历到一个节点的次序作为它的“编号”。事实上,我们管这些“编号”叫做时间戳,记作 D F N [ x ] DFN[x] DFN[x]。
在我们的努力下,这张图有了灵魂:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-80CNaE0u-1594772179319)(https://mrcontinue.github.io/post-images/1591708363762.png)]
搜索树
有了一张有灵魂的图,我们忍不住对它进行了一次遍历。这样,便走出了一棵搜索树(右图):
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hK3CcMRA-1594772179319)(https://mrcontinue.github.io/post-images/1591709091067.png)]
所谓搜索树,就是从无向图的一个节点开始递归,每个店只访问一次,所有可以遍历到的边( x x x, y y y)(换言之,从 x x x到 y y y是对 y y y的第一次访问)构成的一棵树。
追溯值( L O W LOW LOW,就是“你好LOW啊”的那个LOW)
有了一棵搜索树,我们引入一个概念:“追溯值”,记为 L O W [ x ] LOW[x] LOW[x]。设有一棵以 x x x为根的搜索树 s u b t r e e ( x ) subtree(x) subtree(x),则 L O W [ x ] LOW[x] LOW[x]是以下两个范围中节点时间戳的最小值:
- s u b t r e e ( x ) subtree(x) subtree(x)中的节点。
- 可以通过一条边到达 s u b t r e e ( x ) subtree(x) subtree(x)而不在 s u b t r e e ( x ) subtree(x) subtree(x)上的节点。
看到这里别懵啊,不是我的语言艺术不够丰富,是太绕了(确信)举个栗子理解一下吧?
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4FDZ6SYh-1594772179320)(https://mrcontinue.github.io/post-images/1591710169468.png)]
还是上图这张美丽的图。我们用时间戳代表编号。
以节点2为例。 s u b t r e e ( 2 ) subtree(2) subtree(2)={ 2 , 3 , 4 , 5 2,3,4,5 2,3,4,5},然后我们进行第一步,即寻找 s u b t r e e ( 2 ) subtree(2) subtree(2)中的节点的最小值。目前可以得到: L O W [ 2 ] LOW[2] LOW[2]= m i n ( 2 , 3 , 4 , 5 ) min(2,3,4,5) min(2,3,4,5)= 2 2 2。
现在进行第二步,即寻找一个【可以通过一条边到达 s u b t r e e ( 2 ) subtree(2) subtree(2)而不在 s u b t r e e ( 2 ) subtree(2) subtree(2)上的节点】.不难发现节点1符合这样的条件,所以 L O W [ 2 ] LOW[2] LOW[2]= m i n ( 2 , 1 ) min(2,1) min(2,1)= 1 1 1。
聪明的你,一定懂了叭?
紧接着问题来了,怎么计算 L O W LOW LOW值呢?
追溯值( L O W LOW LOW值)的求解
根据定义,为了计算 L O W [ x ] LOW[x] LOW[x],我们应先将 L O W [ x ] LOW[x] LOW[x]的初始值赋为 D F N [ x ] DFN[x] DFN[x]。(为什么?其实是为了方便判断当前节点所连的子树是否为单独的强连通分量。但这已经扯到比较后面了,所以先放一放叭。)接着进行刚刚我们分析了好久的那两步:
- 如果有一节点 y y y在 s u b t r e e ( x ) subtree(x) subtree(x)上,则 L O W [ x ] LOW[x] LOW[x]= m i n ( L O W [ x ] , L O W [ y ] ) min(LOW[x],LOW[y]) min(LOW[x],LOW[y])。
- 如果节点 y y y不在 s u b t r e e ( x ) subtree(x) subtree(x)上,但直接与 s u b t r e e ( x ) subtree(x) subtree(x)相连通时,则 L O W [ x ] LOW[x] LOW[x]= m i n ( L O W [ x ] , D F N [ y ] ) min(LOW[x],DFN[y]) min(LOW[x],DFN[y])。
比较模糊还是有点懵?下面我们一起来举个栗子吧!
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Nr8d6vMQ-1594772179321)(https://mrcontinue.github.io/post-images/1591710169468.png)]
还是上面这张美丽的图。
从节点1开始。初始化 L O W [ 1 ] = D F N [ 1 ] = 1 LOW[1]=DFN[1]=1 LOW[1]=DFN[1]=1, s u b t r e e ( 1 ) subtree(1) subtree(1)={ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 1,2,3,4,5,6,7,8 1,2,3,4,5,6,7,8},无不在 s u b t r e e ( 1 ) subtree(1) subtree(1)上却与 s u b t r e e ( 1 ) subtree(1) subtree(1)直接相连的点。所以 L O W [ 1 ] LOW[1] LOW[1]= m i n ( 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 ) min(1,2,3,4,5,6,7,8) min(1,2,3,4,5,6,7,8)= 1 1 1。
接着遍历节点2。初始化 L O W [ 2 ] = D F N [ 2 ] = 2 LOW[2]=DFN[2]=2 LOW[2]=DFN[2]=2, s u b t r e e ( 2 ) subtree(2) subtree(2)={ 2 , 3 , 4 , 5 2,3,4,5 2,3,4,5}。节点1是不在 s u b t r e e ( 2 ) subtree(2) subtree(2)上却与 s u b t r e e ( 2 ) subtree(2) subtree(2)直接相连的点。所以 L O W [ 2 ] LOW[2] LOW[2]= m i n ( 1 , 2 , 3 , 4 , 5 ) min(1,2,3,4,5) min(1,2,3,4,5)= 1 1 1。
以此类推,我们可以得出下图([]里的数字是节点对应的 L O W LOW LOW值):
T a r j a n Tarjan Tarjan算法简化操作步骤:
-
找一个没有被访问过的节点 u u u;否则,算法结束;(图不连通)
-
初始化 d f n [ u ] dfn[u] dfn[u]和 l o w [ u ] low[u] low[u]
对于u所有的邻接顶点 v v v:- 如果没有访问过,则转到步骤 ( 2 ) (2) (2),同时维护 l o w [ u ] low[u] low[u];
- 如果访问过,但没有删除,维护 l o w [ u ] low[u] low[u];
-
如果 l o w [ u ] low[u] low[u]== d f n [ u ] dfn[u] dfn[u],那么输出相应的强连通分量。
1572 1572 1572 消息的传递 2269 2269 2269
(没有找到大 O J OJ OJ的题目链接,委屈各位大佬了 o r z orz orz)
D e s c r i p t i o n Description Description
我们的郭嘉大大在曹操这过得逍遥自在,但是有一天曹操给了他一个任务,在建邺城内有N(<=1000)个袁绍的奸细,将他们从1到N进行编号,同时他们之间存在一种传递关系,即若C[i,j]=1,则奸细i能将消息直接传递给奸细j。
现在曹操要发布一个假消息,需要传达给所有奸细,而我们的郭嘉大大则需要传递给尽量少的奸细使所有的奸细都知道这一个消息,问我们至少要传给几个奸细
I n p u t Input Input
第一行是两个整数N,M(N<=100,M<=1000),分别表示网络的结点个数和弧数。
第二行至M+1行,每行三个整数A,B,C,表示弧上的损耗为C。
O u t p u t Output Output
输出仅一个整数,为损耗最大的线路的损耗量。
S a m p l e Sample Sample I n p u t Input Input
5 5
1 2 2
2 4 9
1 3 7
3 4 1
4 5 6
S a m p l e Sample Sample O u t p u t Output Output
17
#include ! \color{Red}\colorbox{Yellow}{!} !
无向图的连通性
割点
割点是什么?
割点是一张无向图中非常重要的点。(额……不是废话)在一张连通的无向图中,如果突然少了一个割点,那么这个图就会变得不连通。
其中节点 6 6 6就是割点之一。因为如果没有了节点 6 6 6,这张图就会变成这样:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BqeHmEaM-1594772179323)(https://mrcontinue.github.io/post-images/1591797820993.png)]
这样就易懂很多啦qwq
但是这时候聪明的大佬宁可能要问了,说割点就是“很重要的点”是非常不严谨的不良行为(主要是不利于装 B B B( b u s h i bushi bushi))
(严肃的)概念介绍:割点
- 定义:
在双连通图上, 任何一对顶点之间至少存在有两条路径,在删去某个顶点及与该顶点相关联的边时, 也不破坏图的连通性。如果一个图不是双连通的,那么,将其删除后图将不再连通的那些顶点称为割点。 - 求割点的算法:
我们通过 D F S DFS DFS把无向图定向成有向图,定义每个顶点两个参数:
① d f n [ u ] dfn[u] dfn[u]表示顶点 u u u访问的先后顺序。
②$ lowlink[u] 表 示 沿 表示沿 表示沿u 出 发 的 有 向 轨 能 够 到 达 的 点 出发的有向轨能够到达的点 出发的有向轨能够到达的点v 中 , 中, 中,dfn[v]$值的最小值 (经过返祖边后则停止) - 三个定理
【定理 1 1 1】: D F S DFS DFS中, e = a b e=ab e=ab是返祖边,那么要么 a a a是 b b b的祖先,要么 a a a是 b b b的后代子孙。
【定理 2 2 2】: D F S DFS DFS中, e = u v e=uv e=uv是父子边,且 d f n [ u ] > 1 dfn[u]>1 dfn[u]>1, l o w l i n k [ v ] ≥ d f n [ u ] lowlink[v]≥dfn[u] lowlink[v]≥dfn[u],则 u u u是割点。
【定理 3 3 3】: D F S DFS DFS的根 r r r是割点的充要条件是:至少有 2 2 2条以 r r r为尾(从 r r r出发)的父子边。
4. 求割点的算法:
void DFS(int u)
{
sign++;
dfn[u]=sign; //给u按照访问顺序的先后标号为sign
lowlink[u]=sign; //给lowlink[u]赋初始值
for(int v=1;v<=n;v++) //寻找一个u的相邻节点v
if(MAP[u][v]&&prt[u]!=v) // u→v有边相连且不是回边
{
if(dfn[v]==0) //v未被访问
{
prt[v]=u; //则u是v的父亲
DFS(v); //uv是父子边,递归访问v
lowlink[u]=min(lowlink[u],lowlink[v]);//所有儿子中最小值
if(lowlink[v]>=dfn[u])
{
if(dfn[u]==1)
{
son++;
if(son>=2) cout<<u<<endl;
}//根
else cout<<u<<endl;//u是割点
}
}
else lowlink[u]= min(lowlink[u],dfn[v]);
//若已访问则访问时间一定早于u,uv是返祖边
}
}
割边
割边是什么?
知道了割点是很重要的点,自然,割边就是很重要的边啦~(
别打我QAQ
同样的,如果有一条边突然不见了,能使得整个图变成几个独立的、封闭的部分,则这条边是割边。
又双叒是这个图,我们给每条边起个名字qwq
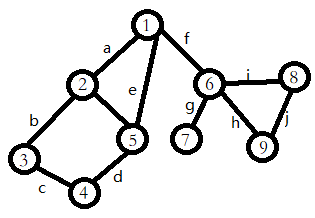
其中边 f f f就是一条割边。因为如果没有了边 f f f,这张图就会变成这样:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-joH3TDcT-1594772179325)(https://mrcontinue.github.io/post-images/1594473843220.png)]
判定割边的方法(部分摘自资料:《算法竞赛进阶指南》)
如果两个节点 x x x、 y y y满足:
d f n [ x ] < l o w [ y ] dfn[x]<low[y] dfn[x]<low[y]
则可以判定边 x y xy xy是一条割边。
根据定义, d f n [ x ] < l o w [ y ] dfn[x]<low[y] dfn[x]<low[y]说明从 s u b t r e e ( y ) subtree(y) subtree(y)出发,在不经过 ( x , y ) (x,y) (x,y)的前提下,不管走哪条边,都无法到达 x x x或比 x x x更早访问的节点。若把 ( x , y ) (x,y) (x,y)删除,则 s u b t r e e ( y ) subtree(y) subtree(y)就好像形成了一个封闭的环境,与节点 x x x没有边相连,图断开成了两部分,因此 ( x , y ) (x,y) (x,y)是割边。
反之,若不存在这样的子节点 y y y,使得 d f n [ x ] < l o w [ y ] dfn[x]<low[y] dfn[x]<low[y],则说明每个 s u b t r e e ( y ) subtree(y) subtree(y)都能绕行其他变到达 x x x或比 x x x更早访问的节点, ( x , y ) (x,y) (x,y)自然就不是割边。
-
割边:
- 定义:
G G G是连通图, e ∈ E ( G ) e∈E(G) e∈E(G), G − e G-e G−e不再连通,则称 e e e是 G G G的割边,亦称做桥。
2.求割边的算法
与割点类似的,我们定义 l o w low low和 d f n dfn dfn。父子边 e = u → v e=u→v e=u→v,当且仅当 l o w [ v ] > d f n [ u ] low[v]>dfn[u] low[v]>dfn[u]的时候, e e e是割边。3.求割边的参考代码:
void DFS(int u) { sign++; dfn[u]=sign; //给u按照访问顺序的先后标号为sign lowlink[u]=sign; //给lowlink[u]赋初始值 for(寻找一个u的相邻节点v) if(边uv没有被标记过) { 标记边uv; 给边定向u→v; if(v未被标记过) { DFS(v); //uv是父子边,递归访问 lowlink[u]=min(lowlink[u],lowlink[v]); if(lowlink[v]>dfn[u])uv是割边 } else lowlink[u]=min(lowlink[u],dfn[v]);//uv是返祖边 } }- 割点与割边
两个割点之间的边不是割边,割边的两端点不是割点。
- 定义:
-
块
1.定义:
没有割点的图叫连通图,亦称做块。把每个块收缩成一个点,就得到一棵树,它的边就是桥。2.求块的算法:
在求割点的算法中,当结点u的所有邻边都被访问过之后,如果存 l o w l i n k [ u ] = d f n [ u ] lowlink[u]=dfn[u] lowlink[u]=dfn[u],我们把 u u u下方的整块和 u u u导出作为图中的一个块。
这里需要用一个栈来表示哪些元素是u代表的块。
关键路径
关于关键路径的相关概念:
定义:在一个给定的有向无环图中,求从开始顶点到结束顶点的最长路径(路径上的
权值和)叫关键路径。
算法步骤:
- 读入数据,建立有向图
- 对 D A G DAG DAG进行拓扑排序,得到拓扑序列
- 以拓扑序列为阶段,用 D P DP DP求关键路径
1570 1570 1570 工厂的烦恼
(仍然没有找到 o r z orz orz)
D e s c r i p t i o n Description Description
某工厂发现厂里的机器在生产产品时要消耗大量的原材料,也就是说,有大量的原材料变成了废物。因此厂里想找出消耗原材料最大的一条生产线路进行改造,以降低成本。厂里的生产线路是一个有向无环网络,有N台机器分别代表网络中的N个结点。弧< I,j >(i < j)表示原材料从机器i传输到机器j的损耗数量。
I n p u t Input Input
文件的第一行为N,第二行至第N+1行为N*N的矩阵(若第I行第J列为1,则奸细I能将消息直接传递给奸细J,若第I行第J列为0,则奸细I不能将消息直接传递给奸细J)。
O u t p u t Output Output
输出文件只有一行:即我们的郭嘉大大首先至少要传递的奸细个数。
S a m p l e Sample Sample I n p u t Input Input
8
0 0 1 0 0 0 0 0
1 0 0 1 0 0 0 0
0 1 0 1 1 0 0 0
0 0 0 0 0 1 0 0
0 0 0 1 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 1 0 0 0 1
0 0 0 0 0 0 1 0
S a m p l e Sample Sample O u t p u t Output Output
2
#include ! \color{Red}\colorbox{Yellow}{!} !
差分约束系统
像这样一类问题:给定一组不等式 x [ i ] − x [ j ] < = c [ k ] x[i]-x[j]<=c[k] x[i]−x[j]<=c[k](或 x [ i ] − x [ j ] > = c [ k ] x[i]-x[j]>=c[k] x[i]−x[j]>=c[k]),需要求出满足所有不等式的一组解( x [ 1 ] , x [ 2 ] , … , x [ n ] x[1],x[2],…,x[n] x[1],x[2],…,x[n])。
这类问题实际上是线性规划的一类简单问题。通常可以用系数矩阵表示为 A x < = C Ax<=C Ax<=C(或 A x > = C Ax>=C Ax>=C),其中系数矩阵 A A A的每一行里有一个 1 1 1和一个 − 1 -1 −1,其余元素都为 0 0 0。若 A A A为 m ∗ n m*n m∗n的矩阵,则 x x x为 n ∗ 1 n*1 n∗1的矩阵, C C C为 m ∗ 1 m*1 m∗1的矩阵,对应有 m m m个不等式, n n n个未知数,即该系统为一个有 n n n个未知数、 m m m个约束条件的系统。这就是差分约束系统。
如果一组解( x [ 1 ] , x [ 2 ] , … . , x [ n ] x[1],x[2],….,x[n] x[1],x[2],….,x[n])满足给定的不等式组,那么( x [ 1 ] + a , x [ 2 ] + a , … . , x [ n ] + a x[1]+a,x[2]+a,….,x[n]+a x[1]+a,x[2]+a,….,x[n]+a)也能够满足,所以这类问题的解不唯一。实际问题中通常对输出的解有一些特别的要求。
自己的一些零碎总结:
-
差分约束系统将题目中的约束条件不等式(即 d [ x ] + w ( x , t ) > = d [ y ] d[x]+w(x,t)>=d[y] d[x]+w(x,t)>=d[y]或 d [ x ] + w ( x , t ) < = d [ y ] d[x]+w(x,t)<=d[y] d[x]+w(x,t)<=d[y]之类)转换为图论的单源最短路问题。
-
当不等式是 d [ x ] + w ( x , t ) > = d [ y ] d[x]+w(x,t)>=d[y] d[x]+w(x,t)>=d[y]时,求最短路;当题目不等式是 d [ x ] + w ( x , t ) < = d [ y ] d[x]+w(x,t)<=d[y] d[x]+w(x,t)<=d[y]时,求最长路。
-
有负权回路的有向图不存在最短路径,即无解。
-
注意建边时是 j j j到 i i i建边,其原因是不等式。
1595 1595 1595 工程规划 1252 1252 1252
D e c i s i o n Decision Decision
造一栋大楼是一项艰巨的工程,它是有n个子任务构成的,给它们分别编号1,2,3,....,n(5<=n<=1000).由于对一些任务的起始条件有着严格地限制,所以每个任务的起始时间T1,T2,T3....,Tn并不是很容易确定的(但这些起始时间都是非负整数,因为它们必须在整个工程开始后启动).例如:挖掘完成后,紧接着就要打地基;但是混泥土浇筑完成后,却要等待一段时间再去掉模板.
这种要求就可以用m(5<=m<=5000)个不等式表示,不等式形如ti-tj<=B代表i和j的起始时间必须满足的条件.每个不等式的右边都是一个常数B,这些常数可能不相同,但是它们都在区间(-100,100)内.
你的任务就是写一个程序,当给定像上面那样的不等式后,找出一种可能的起始时间序列T1,T2,T3....,Tn,或者判断问题无解.对于有解的情况,要使最早进行的哪个任务和整个工程的起始时间,也就是说,T1,T2,T3....,Tn中至少有一个0.
I n p u t Input Input
第一行是用空格分开的两个正整数N和M,下面的M行每行有三个用空格分开的整数i,j,B对应着不等式ti-tj<=B.
O u t p u t Output Output
如果有可行的方案,那么输出N行,每行都有一个非负整数且至少有一个0,按照顺序表示每个任务的起始时间.如果没有可行的方案,就输出信息NO SOLUTION.
S a m p l e Sample Sample I n p u t Input Input
5 8
1 2 0
1 5 -1
2 5 1
3 1 5
4 1 4
4 3 -1
5 3 -3
5 4 -3
S a m p l e Sample Sample O u t p u t Output Output
0
2
5
4
1
#include 后记 by 2020 年 3 月 31 日 20 : 50 : 48 2020年3月31日20:50:48 2020年3月31日20:50:48
由于时间仓促,后面的代码等内容可能没有前面详尽。当然,本蒟蒻在写作过程中肯定有不对之处,还希望大佬们广泛地提出问题,以便我和大家更好的知识掌握。
感谢您的认真观看!
后记 by 2020 年 5 月 6 日 22 : 48 : 11 2020年5月6日22:48:11 2020年5月6日22:48:11
在写作完毕过后自己曾经打印了这份博客作为复习资料,发现里面很多生搬的概念,完全起不到吸收知识的作用。于是乎,我决定慢慢的,从今天起,一点一点润色这篇博客,争取让里面90%的东西都是自己的所思所想。
经过一场考试,抱灵的成绩让我更加意识到了自己吸收知识的重要性……
F i n e , g o o d n i g h t . Fine,good night. Fine,goodnight.
后记 by 2020 年 7 月 12 日 22 : 02 : 37 2020年7月12日22:02:37 2020年7月12日22:02:37
期末考试因为寒假没有好好学,最好成绩全年级 18 18 18名的我,三个主科有两个没有上全年级前 800 800 800。
竞赛这边也要进行分班考试了,可能 300 300 300个人就带走 60 60 60个,还要文化课竞赛课双过关才能进班,没戏了。
没戏了,所有都没戏了,自己一个人自以为是的游戏也应该结束了。
颓废的我,水时间的我,垃圾的我,是时候被大浪淘去了。
我已经习惯了被骂了,习惯了拾起信心,改过自新,又被自己打倒了。我就是生活的痞子,什么都无所谓了。大概只有被人嘲笑,求而不得,缴纳学费的时候,才会有一点痛苦。我已经找不到改过自新的方法了。也许就不该再存在了吧。
希望以后还能和 O I OI OI、信息学科微笑着招手吧。剩下的块、关键路径和差分约束系统可能不会再完善了吧;这篇文章开头“备忘录”里的事大概也不会做了;存在我博客编辑器里那些未公开的文章,大概不会被看到这行字的你看见了吧。
明明没有 A F O AFO AFO,却已经做好 A F O AFO AFO的觉悟了呢。毕竟这就是现实啊。微笑着接受吧。
感谢你看到这里,忍受我这么多的废话。祝你有自己想要的未来,祝你能得到你想得到的,祝你能天天看见你想看见的人,祝你能幸福永远,祝你永远不会成为我。
晚安,再次感谢。
q.pop();
cnt[x]++;
if(cnt[x]>n) {
cout<<"NO SOLUTION"<dis[x]+a[i].w) {
dis[tt]=dis[x]+a[i].w;
if(!v[tt])
q.push(tt),v[tt]=1;
}
}
v[x]=0;
}
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1; i<=m; i++) {
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
AddEdge(y,x,z); //一定注意,是y向x连边
}
memset(dis,127,sizeof(dis));
for(int i=1; i<=n; i++) { //构建虚拟超级源点,所有边都连上
AddEdge(0,i,0);
}
SPFA(0);
if(!fag) {
for(int i=1; i<=n; i++)
kk=min(kk,dis[i]); //寻找最小值
for(int i=1; i<=n; i++)
printf("%d\n",dis[i]-kk);
}
return 0;
}
------------
## 后记 by $2020年3月31日20:50:48$
由于时间仓促,后面的代码等内容可能没有前面详尽。当然,本蒟蒻在写作过程中肯定有不对之处,还希望大佬们广泛地提出问题,以便我和大家更好的知识掌握。
感谢您的认真观看!
-------
## 后记 by $2020年5月6日22:48:11$
在写作完毕过后自己曾经打印了这份博客作为复习资料,发现里面很多生搬的概念,完全起不到吸收知识的作用。于是乎,我决定慢慢的,从今天起,一点一点润色这篇博客,争取让里面90%的东西都是自己的所思所想。
经过一场考试,抱灵的成绩让我更加意识到了自己吸收知识的重要性……
$Fine,good night.$
-------
## 后记 by $2020年7月12日22:02:37$
期末考试因为寒假没有好好学,最好成绩全年级$18$名的我,三个主科有两个没有上全年级前$800$。
竞赛这边也要进行分班考试了,可能$300$个人就带走$60$个,还要文化课竞赛课双过关才能进班,没戏了。
没戏了,所有都没戏了,自己一个人自以为是的游戏也应该结束了。
颓废的我,水时间的我,垃圾的我,是时候被大浪淘去了。
我已经习惯了被骂了,习惯了拾起信心,改过自新,又被自己打倒了。我就是生活的痞子,什么都无所谓了。大概只有被人嘲笑,求而不得,缴纳学费的时候,才会有一点痛苦。我已经找不到改过自新的方法了。也许就不该再存在了吧。
希望以后还能和$OI$、信息学科微笑着招手吧。剩下的块、关键路径和差分约束系统可能不会再完善了吧;这篇文章开头“备忘录”里的事大概也不会做了;存在我博客编辑器里那些未公开的文章,大概不会被看到这行字的你看见了吧。
明明没有$AFO$,却已经做好$AFO$的觉悟了呢。毕竟这就是现实啊。微笑着接受吧。
感谢你看到这里,忍受我这么多的废话。祝你有自己想要的未来,祝你能得到你想得到的,祝你能天天看见你想看见的人,祝你能幸福永远,祝你永远不会成为我。
晚安,再次感谢。