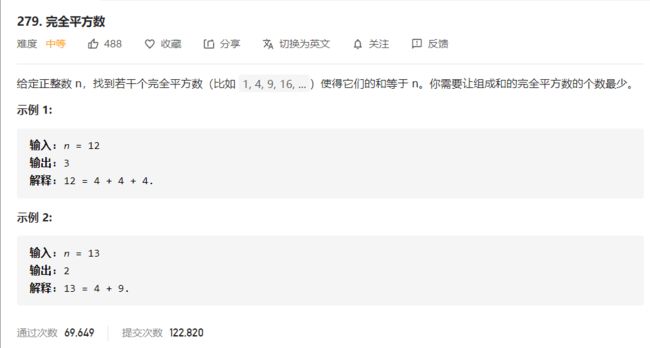
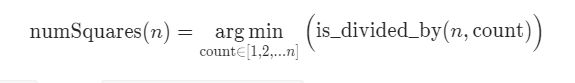【LeetCode】279.完全平方数(四种方法,不怕不会!开拓思维)
题目
链接
题解
方法一:动态规划
思路
1,对于正整数N, 所有的解都是 N = 一个整数的平方 + 另一个整数; 直白点, N = AxA + B
2, 而B又是由 “一个整数的平方 + 另一个整数” 组成的; 那么, B = CxC + D
3,总结下就是:N = IxI + N’ 而 N’ = IxI + N’’
4, 本题要解的问题:正整数N最少由多个平方数相加;
5, 那么,N的最优解 = 1 + (N’的最优解)。而N’肯定小于N。
6, 所以本题的思路就是,对每一个N,观察1到N-1中,谁的解最小,那么N的解就是它+1.
7, 但是我们没必要1到N-1中的每一个数都去观察,因为有些组合不满足N = IxI + N’,譬如12 = 2+N’是不需要的,因为2不是某个数的平方。所以我们观察的范围要大大减小。
拿12举例,我们只能观察:
12 = 1 + 11
12 = 4 + 8
12 = 9 + 3
我们要得出3,8,11中谁的解最优,那么12的解就是它+1。
8, 我们从1到N计算, 2的解从1里找,3的解从[2,1]里找,4的解从[3,2,1]里找,依次类推,最后算到N的解即可。
数学理解
//假设最小公式值m = ƒ(n)
//那么n的值满足下列公式 ∑(A[i] * A[i]) = n
//令 k 为满足最小值 m 的时候,最大的平方数 。 令 d + k * k = n ; d >= 0;
// 注意:一定要是满足m最小的时候的k值,一味的取最大平方数,就是贪心算法了
//得出 f(d) + f(k*k) = f(n);
//显然 f(k*k) = 1; 则 f(d) + 1 = f(n); 因为 d = n - k*k;
//则可以推出ƒ(n - k * k) + 1 = ƒ(n) ; 且 k * k <= n;
我们来理解一下动态规划方程dp[i] = Math.min(dp[i], dp[i - j * j] + 1)
#动态方程的全写版本应该是:
for(int j = 1;j*j<=i;j++){
dp[i] = Math.main(dp[i],dp[i-j*j]+dp[j*j];
}
# dp[i]:表示完全平方数和为i的 最小个数
# 初始状态dp[i]均取最大值i,即 1+1+...+1,i个1; dp[0] = 0
# dp[i] = min(dp[i], dp[i-j*j]+1),其中, j是平方数, j=1~k,其中k*k要保证 <= i
# 意思就是:(完全平方数和为i的最小个数) 等于 (当前完全平方数和为i的最大个数)dp[i] 与 (完全平方数和为 i - j * j 的最小个数 + 完全平方数和为 j * j的 最小个数)的最小个数
# 可以看到 dp[j*j] 是等于1的
class Solution {
public int numSquares(int n) {
int[] dp = new int[n + 1]; // 默认初始化值都为0
for (int i = 1; i <= n; i++) {
dp[i] = i; // 最坏的情况就是每次+1
for (int j = 1; i - j * j >= 0; j++) {
dp[i] = Math.min(dp[i], dp[i - j * j] + 1); // 动态转移方程
}
}
return dp[n];
}
}
方法二:贪心枚举
递归解决方法为我们理解问题提供了简洁直观的方法。我们仍然可以用递归解决这个问题。为了改进上述暴力枚举解决方案,我们可以在递归中加入贪心。我们可以将枚举重新格式化如下:
从一个数字到多个数字的组合开始,一旦我们找到一个可以组合成给定数字 n 的组合,那么我们可以说我们找到了最小的组合,因为我们贪心的从小到大的枚举组合。
为了更好的解释,我们首先定义一个名为 is_divided_by(n, count) 的函数,该函数返回一个布尔值,表示数字 n 是否可以被一个数字 count 组合,而不是像前面函数 numSquares(n) 返回组合的确切大小。
与递归函数 numSquare(n) 不同,is_divided_by(n, count) 的递归过程可以归结为底部情况(即 count==1)更快。
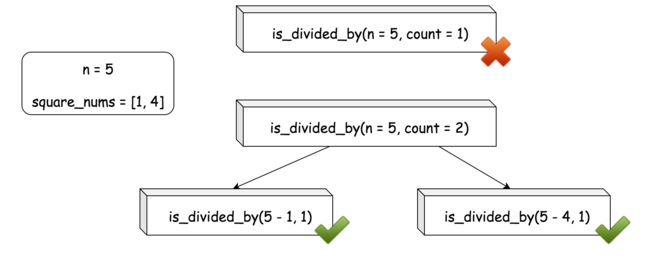
下面是一个关于函数 is_divided_by(n, count) 的例子,它对 输入 n=5 和 count=2 进行了分解。
算法:
- 首先,我们准备一个小于给定数字
n的完全平方数列表(称为square_nums)。 - 在主循环中,将组合的大小(称为
count)从1迭代到n,我们检查数字n是否可以除以组合的和,即is_divided_by(n, count)。 - 函数
is_divided_by(n, count)可以用递归的形式实现,汝上面所说。 - 在最下面的例子中,我们有
count==1,我们只需检查数字n是否本身是一个完全平方数。可以在square_nums中检查,即 n \in \text{square_nums}n∈square_nums。如果square_nums使用的是集合数据结构,我们可以获得比n == int(sqrt(n)) ^ 2更快的运行时间。
关于算法的正确性,通常情况下,我们可以用反证法来证明贪心算法。这也不例外。假设我们发现 count=m 可以除以 n,并且假设在以后的迭代中存在另一个 count=p 也可以除以 n,并且这个数的组合小于找到的数,即 pcount = p 会在 count=m 之前被发现,因此,该算法总是能够找到组合的最小大小。
下面是一些示例实现。Python 解决方案需要大约 70ms,这比当时大约 90% 的提交要快。
class Solution {
Set<Integer> square_nums = new HashSet<Integer>();
protected boolean is_divided_by(int n, int count) {
if (count == 1) {
return square_nums.contains(n);
}
for (Integer square : square_nums) {
if (is_divided_by(n - square, count - 1)) {
return true;
}
}
return false;
}
public int numSquares(int n) {
this.square_nums.clear();
for (int i = 1; i * i <= n; ++i) {
this.square_nums.add(i * i);
}
int count = 1;
for (; count <= n; ++count) {
if (is_divided_by(n, count))
return count;
}
return count;
}
}
复杂度分析
- 时间复杂度: O ( n h + 1 − 1 n − 1 ) = O ( n h 2 ) , \mathcal{O}( \frac{\sqrt{n}^{h+1} - 1}{\sqrt{n} - 1} ) = \mathcal{O}(n^{\frac{h}{2}}), O(n−1nh+1−1)=O(n2h),其中
h是可能发生的最大递归次数。你可能会注意到,上面的公式实际上类似于计算完整 N 元数种结点数的公式。事实上,算法种的递归调用轨迹形成一个 N 元树,其中 NN 是square_nums种的完全平方数个数。即,在最坏的情况下,我们可能要遍历整棵树才能找到最终解。 - 空间复杂度: O ( n ) \mathcal{O}(\sqrt{n}) O(n),我们存储了一个列表
square_nums,我们还需要额外的空间用于递归调用堆栈。但正如我们所了解的那样,调用轨迹的大小不会超过4。
方法三:贪心 + BFS(广度优先搜索)
正如上述贪心算法的复杂性分析种提到的,调用堆栈的轨迹形成一颗 N 元树,其中每个结点代表 is_divided_by(n, count) 函数的调用。基于上述想法,我们可以把原来的问题重新表述如下:
给定一个 N 元树,其中每个节点表示数字 n 的余数减去一个完全平方数的组合,我们的任务是在树中找到一个节点,该节点满足两个条件:
(1) 节点的值(即余数)也是一个完全平方数。
(2) 在满足条件(1)的所有节点中,节点和根之间的距离应该最小。
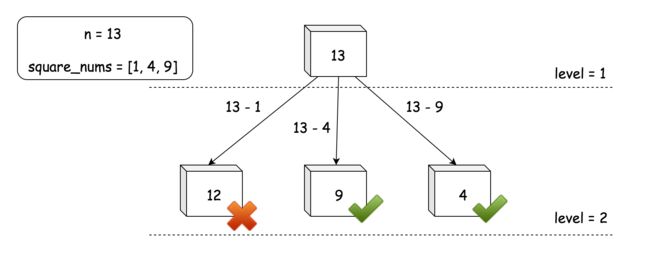
下面是这棵树的样子。
在前面的方法3中,由于我们执行调用的贪心策略,我们实际上是从上到下逐层构造 N 元树。我们以 BFS(广度优先搜索)的方式遍历它。在 N 元树的每一级,我们都在枚举相同大小的组合。
遍历的顺序是 BFS,而不是 DFS(深度优先搜索),这是因为在用尽固定数量的完全平方数分解数字 n 的所有可能性之前,我们不会探索任何需要更多元素的潜在组合。
算法:
- 首先,我们准备小于给定数字
n的完全平方数列表(即square_nums)。 - 然后创建
queue遍历,该变量将保存所有剩余项在每个级别的枚举。 - 在主循环中,我们迭代
queue变量。在每次迭代中,我们检查余数是否是一个完全平方数。如果余数不是一个完全平方数,就用其中一个完全平方数减去它,得到一个新余数,然后将新余数添加到next_queue中,以进行下一级的迭代。一旦遇到一个完全平方数的余数,我们就会跳出循环,这也意味着我们找到了解。
注意:在典型的 BFS 算法中,queue 变量通常是数组或列表类型。但是,这里我们使用 set 类型,以消除同一级别中的剩余项的冗余。事实证明,这个小技巧甚至可以增加 5 倍的运行加速。
在下图中,我们以 numSquares(7) 为例说明队列的布局。
class Solution:
def numSquares(self, n):
# list of square numbers that are less than `n`
square_nums = [i * i for i in range(1, int(n**0.5)+1)]
level = 0
queue = {n}
while queue:
level += 1
#! Important: use set() instead of list() to eliminate the redundancy,
# which would even provide a 5-times speedup, 200ms vs. 1000ms.
next_queue = set()
# construct the queue for the next level
for remainder in queue:
for square_num in square_nums:
if remainder == square_num:
return level # find the node!
elif remainder < square_num:
break
else:
next_queue.add(remainder - square_num)
queue = next_queue
return level
复杂度分析
- 时间复杂度: O ( n h + 1 − 1 n − 1 ) = O ( n h 2 ) , \mathcal{O}( \frac{\sqrt{n}^{h+1} - 1}{\sqrt{n} - 1} ) = \mathcal{O}(n^{\frac{h}{2}}), O(n−1nh+1−1)=O(n2h),其中
h是 N 元树的高度。在前面的方法三我们可以看到详细解释。 - 空间复杂度: O ( ( n ) h ) \mathcal{O}\Big((\sqrt{n})^h\Big) O((n)h),这也是在
h级可以出现的最大节点数。可以看到,虽然我们保留了一个完全平方数列表,但是空间的主要消耗是队列变量,它跟踪给定 N 元树级别上要访问的剩余节点。
方法四:数学运算
随着时间的推移,已经提出并证明的数学定理可以解决这个问题。在这一节中,我们将把这个问题分成几个例子。
1770 年,Joseph Louis Lagrange证明了一个定理,称为四平方和定理,也称为 Bachet 猜想,它指出每个自然数都可以表示为四个整数平方和:
p = a 0 2 + a 1 2 + a 2 2 + a 3 2 p=a_{0}^{2}+a_{1}^{2}+a_{2}^{2}+a_{3}^{2} p=a02+a12+a22+a32
其中 a_{0},a_{1},a_{2},a_{3}a0,a1,a2,a3 表示整数。
例如,3,31 可以被表示为四平方和如下:
3 = 1 2 + 1 2 + 1 2 + 0 2 31 = 5 2 + 2 2 + 1 2 + 1 2 3=1^{2}+1^{2}+1^{2}+0^{2} \qquad 31=5^{2}+2^{2}+1^{2}+1^{2} 3=12+12+12+0231=52+22+12+12
情况 1:拉格朗日四平方定理设置了问题结果的上界,即如果数 n 不能分解为较少的完全平方数,则至少可以分解为 4个完全平方数之和,即 numSquares ( n ) ≤ 4 。 \text{numSquares}(n) \le 4。 numSquares(n)≤4。
正如我们在上面的例子中可能注意到的,数字 0 也被认为是一个完全平方数,因此我们可以认为数字 3 可以分解为 3 个或 4 个完全平方数。
然而,拉格朗日四平方定理并没有直接告诉我们用最小平方数来分解自然数。
后来,在 1797 年,Adrien Marie Legendre用他的三平方定理完成了四平方定理,证明了正整数可以表示为三个平方和的一个特殊条件:
n ≠ 4 k ( 8 m + 7 ) ⟺ n = a 0 2 + a 1 2 + a 2 2 n \ne 4^{k}(8m+7) \iff n = a_{0}^{2}+a_{1}^{2}+a_{2}^{2} n=4k(8m+7)⟺n=a02+a12+a22
其中 k 和 m是整数。
情况 2:与四平方定理不同,Adrien-Marie-Legendre 的三平方定理给了我们一个充分必要的条件来检验这个数是否只能分解成 4 个平方。
从三平方定理看我们在第 2 种情况下得出的结论可能很难。让我们详细说明一下推论过程。
首先,三平方定理告诉我们,如果 n 的形式是$ n = 4^{k}(8m+7)$,那么 n 不能分解为 3 个平方的和。此外,我们还可以断言 n 不能分解为两个平方和,数本身也不是完全平方数。因为假设数 n 可以分解为 n = a 0 2 + a 1 2 n = a_{0}^{2}+a_{1}^{2} n=a02+a12,然后通过在表达式中添加平方数 0,即$ n = a_{0}{2}+a_{1}{2} + 0^2$,我们得到了数 n 可以分解为 3 个平方的结论,这与三平方定理相矛盾。因此,结合四平方定理,我们可以断言,如果这个数不满足三平方定理的条件,它只能分解成四个平方和。
如果这个数满足三平方定理的条件,则可以分解成三个完全平方数。但我们不知道的是,如果这个数可以分解成更少的完全平方数,即一个或两个完全平方数。
所以在我们把这个数视为底部情况(三平方定理)之前,还有两种情况需要检查,即:
情况 3.1:如果数字本身是一个完全平方数,这很容易检查,例如 n == int(sqrt(n)) ^ 2。
情况 3.2:如果这个数可以分解成两个完全平方数和。不幸的是,没有任何数学定理可以帮助我们检查这个情况。我们需要使用枚举方法。
算法:
可以按照上面的例子来实现解决方案。
- 首先,我们检查数字
n的形式是否为$ n = 4^{k}(8m+7)$,如果是,则直接返回 4。 - 否则,我们进一步检查这个数本身是否是一个完全平方数,或者这个数是否可以分解为两个完全平方数和。
- 在底部的情况下,这个数可以分解为 3 个平方和,但我们也可以根据四平方定理,通过加零,把它分解为 4 个平方。但是我们被要求找出最小的平方数。
class Solution {
protected boolean isSquare(int n) {
int sq = (int) Math.sqrt(n);
return n == sq * sq;
}
public int numSquares(int n) {
// four-square and three-square theorems.
while (n % 4 == 0)
n /= 4;
if (n % 8 == 7)
return 4;
if (this.isSquare(n))
return 1;
// enumeration to check if the number can be decomposed into sum of two squares.
for (int i = 1; i * i <= n; ++i) {
if (this.isSquare(n - i * i))
return 2;
}
// bottom case of three-square theorem.
return 3;
}
}
复杂度分析
- 时间复杂度: O ( n ) \mathcal{O}(\sqrt{n}) O(n),在主循环中,我们检查数字是否可以分解为两个平方和,这需要$ \mathcal{O}(\sqrt{n}) $个迭代。在其他情况下,我们会在常数时间内进行检查。
- 空间复杂度: O ( 1 ) \mathcal{O}(1) O(1),该算法消耗一个常量空间。