LeetCode第179场周赛

5352. 生成每种字符都是奇数个的字符串

给你一个整数 n，请你返回一个含 n 个字符的字符串，其中每种字符在该字符串中都恰好出现 奇数次 。

返回的字符串必须只含小写英文字母。如果存在多个满足题目要求的字符串，则返回其中任意一个即可。

示例 1：

输入：n = 4
输出："pppz"
解释："pppz" 是一个满足题目要求的字符串，因为 'p' 出现 3 次，且 'z' 出现 1 次。当然，还有很多其他字符串也满足题目要求，比如："ohhh" 和 "love"。

public class Solution {
    public static String generateTheString(int n) {
        String str = "";
        StringBuilder builder = new StringBuilder(str);
        int index = 0;
        while (index < n) {
            builder.append("a");
            index++;
        }
        if (n % 2 == 0) {
            builder.replace(n - 1, n, "b");
        }
        return builder.toString();
    }
}

5353. 灯泡开关 III

房间中有 n 枚灯泡，编号从 1 到 n，自左向右排成一排。最初，所有的灯都是关着的。

在 k  时刻（ k 的取值范围是 0 到 n - 1），我们打开 light[k] 这个灯。

灯的颜色要想 变成蓝色 就必须同时满足下面两个条件：

• 灯处于打开状态。
• 排在它之前（左侧）的所有灯也都处于打开状态。

请返回能够让 所有开着的 灯都 变成蓝色 的时刻 数目 。

示例 1：

输入：light = [2,1,3,5,4]
输出：3
解释：所有开着的灯都变蓝的时刻分别是 1，2 和 4 。

        这道题，乍一看不太好想，实际上如果理清题意，其实非常简单。注意：所有灯亮蓝灯的条件 实际上 也就是如果处于打开状态的灯的索引的最大值和打开灯的数量相等。

public class Solution {
    //方法1
    public int numTimesAllBlue(int[] light) {
        int result = 0;
        Queue queue = new LinkedList<>();
        Set set = new HashSet<>();
        for (int i = 1; i <= light.length; i++) {
            queue.offer(i);
        }
        int max = Integer.MIN_VALUE;
        for (int i = 0; i < light.length; i++) {
            if (light[i] > max) {
                max = light[i];
            }
            set.add(light[i]);
            while (set.contains(queue.peek()) && max == i + 1) {
                if (light[i] == queue.peek()) {
                    result++;
                }
                queue.poll();

            }
        }
        return result;
    }

    //方法2（简化）
    public static int numTimesAllBlue(int[] light) {
        int maxLight = 0;
        int ans = 0;
        for (int i = 1; i <= light.length; i++) {
            maxLight = Math.max(maxLight, light[i-1]);
            if (maxLight == i) {
                ans++;
            }
        }
        return ans;
    }
}

 5354. 通知所有员工所需的时间

公司里有 n 名员工，每个员工的 ID 都是独一无二的，编号从 0 到 n - 1。公司的总负责人通过 headID 进行标识。

在 manager 数组中，每个员工都有一个直属负责人，其中 manager[i] 是第 i 名员工的直属负责人。对于总负责人，manager[headID] = -1。题目保证从属关系可以用树结构显示。

公司总负责人想要向公司所有员工通告一条紧急消息。他将会首先通知他的直属下属们，然后由这些下属通知他们的下属，直到所有的员工都得知这条紧急消息。

第 i 名员工需要 informTime[i] 分钟来通知它的所有直属下属（也就是说在 informTime[i] 分钟后，他的所有直属下属都可以开始传播这一消息）。

返回通知所有员工这一紧急消息所需要的 分钟数 。

 

 

示例 1：

输入：n = 1, headID = 0, manager = [-1], informTime = [0]
输出：0
解释：公司总负责人是该公司的唯一一名员工。

示例 2：

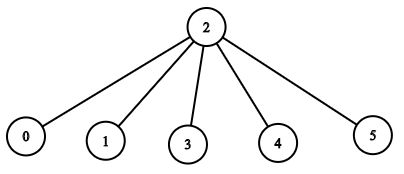
输入：n = 6, headID = 2, manager = [2,2,-1,2,2,2], informTime = [0,0,1,0,0,0]
输出：1
解释：id = 2 的员工是公司的总负责人，也是其他所有员工的直属负责人，他需要 1 分钟来通知所有员工。
上图显示了公司员工的树结构。

        注意结点访问的顺序。对于这道题来说，比较好的方法是自底向上由叶子追溯到根。

public class Solution {
    public int numOfMinutes(int n, int headID, int[] manager, int[] informTime) {
        int res = 0;
        for(int i = 0; i < manager.length; i++) {
            //判断是否为叶子结点，从叶子结点开始遍历
            if(informTime[i] == 0) {
                int temp = 0;  //当前的分钟数
                int index = i;  //结点下标
                //向上遍历，直到根结点
                while(index != -1) {
                    temp += informTime[index];
                    index = manager[index];
                }
                res = Math.max(res, temp);  //所有叶到根的最大值
            }
        }
        return res;
    }
}

5355. T秒后青蛙的位置

给你一棵由 n 个顶点组成的无向树，顶点编号从 1 到 n。青蛙从 顶点 1 开始起跳。规则如下：

• 在一秒内，青蛙从它所在的当前顶点跳到另一个 未访问 过的顶点（如果它们直接相连）。
• 青蛙无法跳回已经访问过的顶点。
• 如果青蛙可以跳到多个不同顶点，那么它跳到其中任意一个顶点上的机率都相同。
• 如果青蛙不能跳到任何未访问过的顶点上，那么它每次跳跃都会停留在原地。

无向树的边用数组 edges 描述，其中 edges[i] = [fromi, toi] 意味着存在一条直接连通 fromi 和 toi 两个顶点的边。

返回青蛙在 t 秒后位于目标顶点 target 上的概率。

示例 1：

输入：n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4
输出：0.16666666666666666 
解释：上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳，第 1 秒 有 1/3 的概率跳到顶点 2 ，然后第 2 秒 有 1/2 的概率跳到顶点 4，因此青蛙在 2 秒后位于顶点 4 的概率是 1/3 * 1/2 = 1/6 = 0.16666666666666666 。 

        注意：无向图的构建，可以采用Map的形式来存储路径信息。

class Solution {
    public double frogPosition(int n, int[][] edges, int t, int target) {
        boolean[] visited = new boolean[n + 1];
        Map> map = new HashMap<>();  //存储路径信息
        for (int[] e: edges) {  //遍历数组，构建无向图
            map.putIfAbsent(e[0], new LinkedList<>());  //如果存在重复的key，那么不会放入值
            map.get(e[0]).add(e[1]);
            map.putIfAbsent(e[1], new LinkedList<>());
            map.get(e[1]).add(e[0]);
        }
        return dfs(map, visited, t, target, 1, 1);
    }

    public double dfs(Map> map, boolean[] visited, int t, int target, int cur, double p) {
        if (t < 0) {
            return 0;
        }
        List next = map.getOrDefault(cur, Collections.emptyList()).stream().filter(i -> !visited[i]).collect(Collectors.toList());
        if (t == 0 || next.size() == 0) {
            return cur == target ? p : 0;
        }
        double res = 0;
        p /= next.size();  //跳到下一个顶点的概率
        visited[cur] = true;
        for (Integer n: next) {
            if ((res = dfs(map, visited, t - 1, target, n, p)) > 0) {
                return res;
            }
        }
        visited[cur] = false;
        return 0;
    }
}