2020年3月25日华为实习生机试编程题

2020年3月25日，华为的实习生机试编程题。

我自己不是计算机科班出身，包括C++、数据结构、算法等并不是我的强项。虽然最后都AC了，但是代码可能都比较丑陋，不管怎么说还是简单记录一下。

第一题

利用两个IP地址与一个子网掩码与来判断这两个IP地址是否处于同一个网段。例如一个IP地址192.168.1.1的二进制形式为…，然后一个子网掩码255.255.255.240的二进制形式为…，按位与的结果为192.168.1.0，二进制形式为…。同网段的IP地址按位与的结果也相同。

输入：IP₁，IP₂，子网掩码 ，三个字符串用空格隔开，保证输入合法。

输出：1 or 0（IP₁和IP₂是否同网段） IP₁与子网掩码按位与的结果

例：

输入：192.168.1.1 192.168.1.1 255.255.255.240

输出：1 192.168.1.0

这题其实主要还是一个字符串的分割，按位与。

我就是这种基础及其薄弱，举个例子，当时我试图用以下这样的语法，发现编译器报错：

int a,b;
cout<<a&b<<endl;

然后我一度以为我是不是连与、或都记错了。反正当时弄得我有点烦躁，直接按照字符串一位位写，总之一言难尽。

#include 
#include 
#include 
using namespace std;

//用于分割字符串并转到int型,对"192.168.1.1"返回[192,168,1,1]的vector
vector<int> split(string s, string delim) {
	vector<int> res;
	string::size_type pos1, pos2 = 0;
	while (pos2!=s.npos)
	{
		pos1 = s.find_first_not_of(delim, pos2);
		if (pos1 == s.npos)
			break;
		pos2 = s.find_first_of(delim, pos1);
		res.push_back(stoi(s.substr(pos1, pos2 - pos1)));
	}
	return res;
}

constexpr auto NUM = 4;;
int main() {
	string ip1, ip2, sm;
	while (cin >> ip1 >> ip2 >> sm)
	{
        //分割字符串保存
		vector<int> v1, v2, v3;
		string delim(".");
		v1 = split(ip1, delim);
		v2 = split(ip2, delim);
		v3 = split(sm, delim);
		
        //按位与
		vector<int> res1, res2;
		for (size_t i = 0; i < NUM; i++)
		{
			res1.push_back(v1[i] & v3[i]);
			res2.push_back(v2[i] & v3[i]);
		}
        
        //判断相等
        int flag = 1;
		for (size_t i = 0; i < NUM; i++)
		{
			if (res1[i] != res2[i]) {
				flag = 0;
				break;
			}
		}
		cout << flag << ' ';
        
        //输出IP1的与结果
		for (size_t i = 0; i < NUM-1; i++)
		{
			cout << res1[i] << '.';
		}
		cout << res1[3] << endl;

	}
    return 0;
}

第二题

求一个01组成的矩阵中，1构成的最大正方形面积。

输入：M个N长的字符串，代表M*N矩阵

输出：最大正方形的面积

例：

输入：“00100111” “11100111” “01100111” ”10100100“

即：

0	0	1	0	0	1	1	1
1	1	1	0	0	1	1	1
0	1	1	0	0	1	1	1
1	0	1	0	0	1	0	0

输出：9

动态规划，以正方形的右下角表示该正方形的边长。建立一个与输入相同大小的二维数组，其中每一点的值都表示以该点作为右下角的正方形边长。

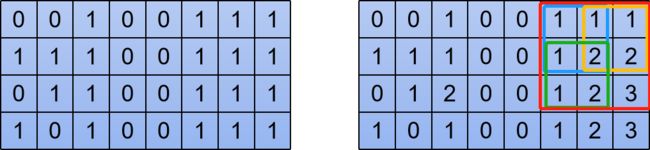
以上面的输入为例，下图中左边是输入，右边是对应的DP矩阵。由于是从左上角往右下角建立的DP关系，可以看到，对于边长为N的正方形，满足以下条件：

// 若DP[i][j]=N，则DP[i-1][j-1]=N-1;DP[i][j-1]=N-1;DP[i-1][j]=N-1;

// 因此先初始化第一行、第一列与输入相同。从（1,1）位置开始，填充剩余部分。
// 对于输入为0的点直接置0跳过，其余位置的动态转移方程。
DP[i][j]=min(DP[i-1][j-1],DP[i][j-1]，DP[i-1][j])

#include 
#include 
#include 
using namespace std;

int main{
    int N;
	while (cin>>N)
	{
		vector<string> matrix(N);
		for (size_t i = 0; i < N; i++)
		{
			cin >> matrix[i];
		}
		int M = matrix[0].size();
        //初始化DP矩阵
		vector<vector<int>> dp;
		for (size_t i = 0; i < N; i++)
		{
			vector<int> dp_(M);
			dp.push_back(dp_);
		}
        //初始化列
		int maxsqlen = 0;
		for (size_t i = 0; i < N; i++)
		{
			dp[i][0] = matrix[i][0]-'0';
			if (dp[i][0] > maxsqlen)
				maxsqlen = dp[i][0];
		}
        //初始化行
		for (size_t i = 0; i < M; i++)
		{
			dp[0][i] = matrix[0][i] - '0';
			if (dp[0][i] > maxsqlen)
				maxsqlen = dp[i][0];
		}
        //求解DP
		for (size_t i = 1; i < N; i++)
		{
			for (size_t j = 1;j < M;j++) {
				if (matrix[i][j] == '1') {
					dp[i][j] = min(min(dp[i - 1][j - 1], dp[i - 1][j]), dp[i][j - 1]) + 1;
					maxsqlen = maxsqlen > dp[i][j] ? maxsqlen : dp[i][j];
				}
			}
		}
		cout << maxsqlen * maxsqlen << endl;
	}
}

第三题

很长的题目，大意是：

有m个cpu，负责n个任务，n个任务分别耗时t1,t2,…,tn。

1、每个cpu同一时间只能处理一个任务，处理完后开始处理新的任务。

2、总是优先处理耗时较短的任务

求解处理完所有任务所需时间。

输入：第一行m n，第二行t1 t2…tn。

输出：耗时

例：

输入：

3 5

8 1 3 4 10

输出：

13

利用std算法库可以快速AC，主要是一个排序的问题。

#include 
#include 
#include 
#include 
using namespace std;

int main(){
    int m, n;
	while (cin>>m>>n)
	{
		vector<int> task(n);
		for (int i = 0;i < n;i++)
			cin >> task[i];
        // 首先对任务处理时间排序
		sort(task.begin(),task.end());
		vector<int> cpu_queen(m);
		for (int i = 0;i < n;i++) {
			cpu_queen[0] += task[i];
            // 对任务处理队列排序，其实每次只需要调整第一个值，插入到后面，可以手写
			sort(cpu_queen.begin(), cpu_queen.end());
		}
		cout << cpu_queen[m-1] << endl;
	}
}