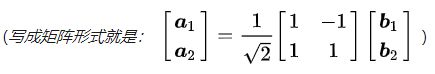量子力学 or 线性代数(二)
线性代数与量子力学的前世今生(二)
- 不确定性原理初体验
- 一. 背景介绍
- 二. 棒棒糖解释
- 三. 棒棒糖的解释和延伸
- 四,棒棒糖的数学解释(线性代数之基底变换)
不确定性原理初体验
OK,上一篇我们以一只可怜的(ΦωΦ)为入手点,向小伙伴们简单的介绍了一下量子力学的入门,以及最重要的: 量子力学与线性代数中千丝万缕 联系中的一小部分。。。还没有点关注的盆友们, 用你们发财的小手指 点个赞,点不了吃亏,点不了上当,你们的鼓励是笔者前进的最大动力~~
一. 背景介绍
作为一名小白,我对于一个新概念的学习理解过程是这样的:先了解它诞生的历史背景,是谁发现或者创造了它, 其次,我们再去了解它 的定义,物理数学含义以及应用等等。。
不确定性原理”有另外一个名字:“测不准原理”。
1926年,海森堡任聘为哥本哈根大学尼尔斯·波耳研究所的讲师,协助尼尔斯·波耳做研究,隔年,他发表了论文《论量子理论运动学与力学的物理内涵》 (On the physical content of quantumtheoretical kinematics and mechanics),在网上找了好久才找到这个珍贵的图片,吐血!!

在这篇论文里提到,使用显微镜来测量电子的位置,需要通过测量光子,会不可避免地搅扰了电子的动量,造成动量的不确定性(其实是这个解释是错的 ):
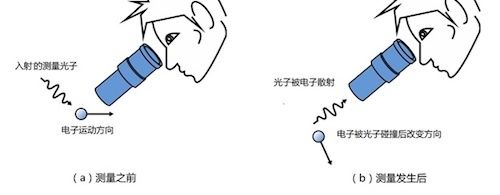
后来啊,在一群智商爆表的大牛们的高逼格数学推理和实验证明之后,将 测不准原理改名为: 不确定性原理
在量子力学中,不确定原理意为:一个运动粒子的位置和它的动量不可被同时确定(由于证明比较复杂,在这里就不展开论述,还是以简单的例子帮助小伙伴们理解!)
二. 棒棒糖解释
现在,请你绞尽脑汁的回想一下你童年时候的“美好”场景:吃棒棒糖。。。。(插个小段子,我小的时候,经常一个人,买一个棒棒糖,拿起一个小凳子,坐在凳子上,轻轻的剥开糖纸,小时候我总认为用力的话会把糖的甜味也剥走了,O(∩_∩)O哈哈~,把舌头伸出来一点一点的舔,千万不能用舌根,聪明的我小时候就发现舌尖才是对甜味最敏感的地方 嘻嘻 ~,一舔就是一下午,哎!长大了,幸福的实现越来越难!!),OK闲话少叙。
首先,大方的我给了你一根神奇的 棒棒糖,神奇之处在于:它的味道有时是甜的,有时是酸的;它的颜色有时是红的,有时是蓝的,你是不是想到了什么,对对对,它就像爱情的味道,酸酸甜甜,o( ̄︶ ̄)o,哇啊~。
醒醒吧,你在想p吃,母胎单身二十年了 ,单身狗!我呸!!
在吃这个糖的时候,你也要像我一样,慢慢的舔,千万不能一口吃完!!
第一次:轻轻的(像我一样)剥开糖纸,像对待爱情一样,慢慢的放到舌尖上,用体温融化它,结果,tm的是酸的。。。。
 |
 |
|---|
第二次:被 爱情 欺骗了的你 立马把棒棒糖从嘴里拿出来了,这时候诡异的事情发生了,这糖变成了红色,WHAT!!是不是和你女盆友的脸色一样,说变就变,抱着岂因祸福避趋之的大义精神你 又把糖放进了嘴里(毕竟有女朋友总比没有好,(* ̄rǒ ̄)),这时候,woc ,变成甜的了,于是,你又相信 爱情 了,呕(⊙o⊙)…
 |
 |
|---|
玩笑归玩笑,经过多次这样的尝试 ,你发现了神马?
1. 每尝一次味道后,糖的颜色就会变;而每看一次颜色后,糖的味道就会变
2. 每次尝完糖的味道之后重新观察它的颜色,变色和不变色的情况各占一半;同样,每次看完糖的颜色之后重新品尝它的味道,变味和不变味的情况也各占一半。
3. 如果我们尝完糖的味道之后,不睁开眼睛观察糖的颜色,那么即使我们把糖拿出来再放进嘴里尝味道,它的味道也不会变,无论重复多少次都不会变;颜色也一样,只要我们不去尝味道,那么我们无论多少次重复观察糖的颜色,它都还是原来的样子。
三. 棒棒糖的解释和延伸
我们再回首到那个猫,对,我们已经回首那只猫无数次了,但是,每一次的感悟肯定都是不一样的,没毛病吧,老铁!!
当我们没有打开盒子去观察猫的状态时,它处于生和死的叠加态,而一旦我们去观察,它就会(从叠加态)随机坍缩到生或死中的一个确定状态(本征态),此后再去观察时,它的状态就不再会改变。
类比过来,我们可以这样认为:
当我们观察了棒棒糖的颜色之后,颜色也会变成红或蓝中的一个确定状态,以后只要不做其他干扰,那么再无论观察多少次,颜色都不会再改变;
或者我们品尝了棒棒糖的味道之后,味道也会变成甜或酸中的一个确定状态,以后只要不做其他干扰,无论再品尝多少次,味道都不会再改变.
当然,这不是最重要的,最重要的是:我们 舔 和 看 一起作用到棒棒糖,就tm见了鬼了:
当我们确定了糖的颜色之后,再去品尝糖的味道,味道又会随机坍缩到酸或甜两种状态,且概率各半;反过来,确定味道之后再去观察颜色,也有同样的情况。
用逼格高一点的话来解释就是:
糖的颜色处于确定状态时,味道就处于不确定的叠加态;而味道处于确定状态时,颜色就会处于不确定的叠加态。

我们现在用量子力学的方法来尝试解答疑惑:
棒棒糖味道的本征态就是 酸 和 甜,分别用 ∣ α 1 > , ∣ α 2 > |\alpha _{1}> ,|\alpha _{2}> ∣α1>,∣α2>来表示。
而棒棒糖的颜色的本征态就是 蓝色 和 红色 ,分别用 ∣ b 1 > , ∣ b 2 > |b _{1}> ,|b _{2}> ∣b1>,∣b2>来表示。
进而解释为:当颜色处于 ∣ b 1 > , ∣ b 2 > |b _{1}> ,|b _{2}> ∣b1>,∣b2>本征态中的一个时,此时味道处于叠加态,此时去重新观测味道,会分别以 1 2 \frac{1}{2} 21的概率得到 酸 ∣ α 1 > |\alpha _{1}> ∣α1> 和 甜 , ∣ α 2 > ,|\alpha _{2}> ,∣α2>的 状态,同样,颜色和味道调换反过来也是一样的。
四,棒棒糖的数学解释(线性代数之基底变换)
回头看看标题,线性代数 or 量子力学?怎么还没出现人见人爱的 线代呢?别急,它这不是来了么。
我们重新假设二维平面中有2组正交的基底向量,分别是 { α 1 , α 2 \alpha _{1}, \alpha _{2} α1,α2},{ b 1 , b 2 b _{1},b _{2} b1,b2}, 它们在同一平面上成45度夹角,如图:
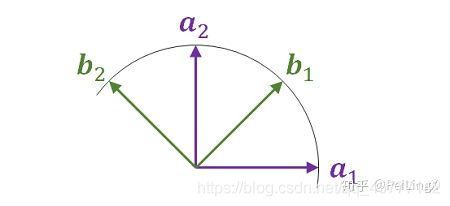
用其中一组来表示另外一组为: { a 1 = 1 2 ( b 1 − b 2 ) a 2 = 1 2 ( b 1 + b 2 ) \left\{ \begin{aligned} a_{1}& = & \frac{1}{\sqrt{ 2}}(b_{1} -b_{2}) \\ a_{2}& = & \frac{1}{\sqrt{ 2}}(b_{1} +b_{2}) \\ \end{aligned} \right. ⎩⎪⎪⎨⎪⎪⎧a1a2==21(b1−b2)21(b1+b2)
如上图所示, α 1 , α 2 \alpha _{1}, \alpha _{2} α1,α2 这二个正交的基底向量可以代表 酸和甜 这2个本征态,除此之外,我们再加上一组正交的基底向量 b 1 , b 2 b _{1},b _{2} b1,b2来表示 蓝色和红色这2个本征态。
根据上面的图示,我们可以直接写出 ∣ a 1 > = 1 2 ( ∣ b 1 > − ∣ b 2 > ) |a_{1}> = \frac{1}{\sqrt{ 2}}(|b_{1}> -|b_{2}>) ∣a1>=21(∣b1>−∣b2>),即当 糖的味道这个物理量已经观测出来结果之后,颜色还是处在叠加态之中,以同样的方式再来测量颜色,那么各自的概率又是多少呢?
这里,我们有将用的上一节讲的内积的应用:
P ( ∣ b 1 > ) = ( 1 2 ) 2 = 1 2 , P ( ∣ b 2 > ) = ( − 1 2 ) 2 = 1 2 P(|b_{1}>) = (\frac{1}{\sqrt{ 2}})^{2} = \frac{1}{2} , P(|b_{2}>) = (-\frac{1}{\sqrt{ 2}})^{2} = \frac{1}{2} P(∣b1>)=(21)2=21,P(∣b2>)=(−21)2=21
这样,我们就能各以1/2的概率得到颜色的结果。。至此,数学解释就算是完成了。
都看到这了,就麻烦您下发点个赞吧!!ε=(´ο`*))),您的每一个赞都是我前进的中流砥柱!!