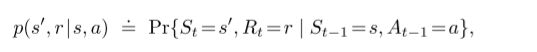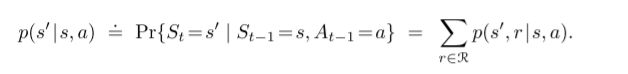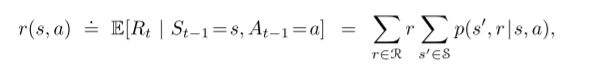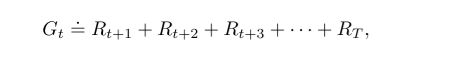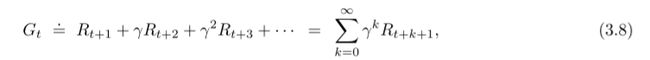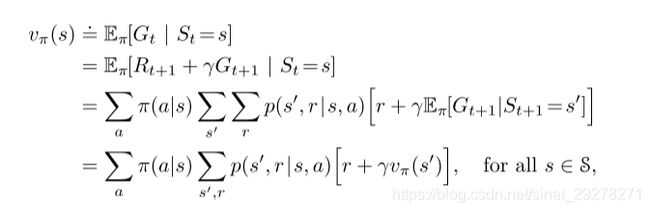强化学习第三章总结（一个简单的总结，因为没时间敲公式，先放在这里，之后慢慢收拾）

MDPs are a classical formalization of sequential decision making, where actions influence not just immediate rewards, but also subsequent situations, or

states, and through those future rewards.

 

 

 

 

 

 

 

 

The Agent Environment Interface

 

 

 

 

 

 

 

强化学习的目的是从交互中学习如何实现一个目标。

 

Learner 或者说决策者被称为agent。Agent交互的对象被称为环境。Agent 选择一个动作，环境给出rewards并更新state。agent的目标是最大化rewards。

 

更确切的说，agent和environment在一个离散的时间部署上进行交互t=1,2,3,4,5。在每个时间部署上，agent收到一个环境的状态的表示, $S_t \in S$, 然后agent选择一个动作， $A_t \in Action(s)$，这里意思是说，在s状态下所有能做的动作。一个时间步数之后，Agent收到一个奖励，

这里第二个R是奖励集合，奖励集合是一个标量，是实数集的子集，随后agent 切换到下一个状态S_{t+1},这个过程循环往复会产生一个时间序列。

 

 

在一个有限的 MDP中，state集合，action集合，rewards集合数量都是有限的，也就是说，

都是有限集合。在这个条件下，我们的R_t和S_t实际上是在已经执行的action和state上定义了一个离散的概率分布。也就是，

 

等号上面的点代表这是一个定义。

 

这是个条件概率分布，所以这应该是一个显然的事情。

 

 

reward和state 的要求：

 

 

state要满足的是马尔可夫性质，在这本书中我们都会假设满足马尔可夫过程。

 

有了这个p函数之后，你会发现，你想要的任何仅与环境相关的东西都可以从这个函数中计算出来，换句话说，这个p函数直接定义了这个environment本身。

比如你想算当前状态s下做一个动作a，下一个状态时s’的概率是多少。

比如你想算当前状态s下，你做了一个动作a，你获得的奖励的期望是多少

 

 

environment和agent的界限有时候可能不那么明确，比如我们当我们考虑一个机器人的时候，他的传感器就应该被视为是环境，尽管传感器是机器人的一部分；当我们考虑一个人的时候，他的肌肉，骨架，和感知器官应该被视为是环境的一部分，哪怕奖励是人的内部产生的，一部分，也应该被视为是由环境提供的。

一言以蔽之，环境就是哪些不能由agent随意修改的东西。agent和environment的界限是agent能完美控制的领域，而不是他的知识覆盖的领域。

 

在不同的地方，可能agent和environment的区别会很大，比如一个很复杂的机器人中，上层的agent做出的决策可能是下层agent面对的环境。

 

MDP框架实际上在说的事情是，无论一个目标导向的学习有多么复杂，都可以分解为三个信号，一个是agent做出的选择，一个是agent做出选择的环境，还有一个是环境给的奖励。

 

3.2 目标和奖励

agent的目标在强化学习中被成为reward，从环境中传递给agent。每个时间步，奖励R_t是一个实数，而agent的目标是最大化累计reward。也就是说，并不是最大化即时奖励，而是在长长的过程中的累计奖励。

 

书上提了一个奖励假设。

 

用奖励信号去formalize目标这个想法是强化学习的一个特征。

 

将目标形式化为一个奖励信号也许看上去有一些局限新，但在实践中发现，这件事挺灵活的，而且适用范围很广。后面有几个乱七八糟的例子，比如让一个机器人学会走路，就让奖励和机器人前进的步数成正比。让机器人学会走出迷宫，就让每一个时间步的奖励为-1，这样子机器人就会学会尽可能快地走出来；想让机器人许会收集苏打水的瓶子，就收集一个苏打水罐子奖励一个+1，其他时候是0，当然你还可以选择在机器装上一个东西或者当别人冲他大喊大叫（撞上人了）的时候获得一个负值的奖励。如果想让agent学会下棋，那你就赢了+1，输了-1。

 

无论你设置的奖励是什么，agent在学习的过程中都会最大化奖励。而你要做的就是让最大化奖励和你的目标是一致的。然后又是一个例子，比如你要你的agent学会下棋，那最好单纯就是赢了+1，输了-1，不要给一些sub-goa比如吃一个棋子奖励。否则可能他会弄出一些玄学操作去做这个子目标。奖励信号的意义是告诉agent你希望他做什么，而不是你希望他怎么做。

 

3.3 Returns and Episodes

我们刚刚说了，我们最终的目标是累计的奖励而不是实时的奖励，但目前我们手头只有一个奖励的序列。也就是R_{t+1}, R_{2+t}, R_{3+t}, …, R_{4+t}

 

一个最简单的例子就是

直接把所有的奖励加起来，这里的T表示终止的时间点。这个想法靠谱的条件是，我们的交互过程有一个显式的终止时间步，也就是说，agent和环境的交流可以被分解成若干个子序列，我们管这个叫episodes。比如玩游戏，迷宫旅行，或者其他一些会重复的交互过程。每个episode 都有一个终止状态叫做terminal state。然后我们就会回到之前的那个标准的起点或者按照一个标准分布选取一个起点。也就是，无论上一个episode最终结局是什么样的，下一个episode与前一个episode都是独立的。从这个角度讲，我们也可以认为每个epsisode最终都在同一个termianl state结束，只是不同的episode 最终的奖励值不一样。我们将非终止状态的集合表示为S，包含了终止状态的集合表示为S^+。T是一个在不同的episode中不同的随机变量。

 

但是在某些情况下，agent和environment的交互是永无止境的。比如一些不间断的任务，一个生命周期很长的机器人之类的（不知道怎么翻译application）。这样一来之前定义的G_t就不好用了，因为T有可能趋近于无穷。，在这个情况下，return G_t本身也有可能是无穷的。

所以，这里要采用一个稍微复杂一点点的return的定义。

这里的 gamma 是折扣因子。要给[0, 1]之间的实数。

 

当折扣因子=1时，这个agent是短视的， gamma 趋近于1时，这个agent变得越来越远视。

 

我们的奖励公式也可以写成上面这个样子，这个形式可以给计算带来很多方，即使t+1时间就是终止状态了，我们也可以通过定义G_{T}为0,来使得这个公式适用。

 

同时我们也可以注意到，当γ<1时，G_t永远都是有限的。

 

3.4 Unified Notation for Episodic and Continuing Tasks

 

这本书的余下部分会讨论两种强化学习任务，一种是agent-environment交互能分割成若干个episodes，另一种是无法分割的。前一种会简单一点，因为一个动作只影响有限种操作。

 

一般来说能分裂成若干个episode 的训练过程要写成S_{t, i},i代表第几段episode。

我们认为有限长度的episode后面跟着无限个为0的R，也就是在终止状态以100%的概率转移到自身并且奖励为0.

 

 也就是下面这张图这样。

 

3.5 Policy and value Functions

 

这里引入了两个新概念 policy

 

 

Π是将一个state映射到action的概率上Π（a|s）。

另一个是价值函数

以及q函数

书上有两个练习，可以等会儿做一下。

 

 

然后，V函数和q函数是能够通过经验获得的，你可以在某个策略下不断采样，将每个状态得到的returns做平均存起来，这样子这些平均值最后就会收敛到q函数或是v函数。这个方法叫做蒙特卡洛方法。当然，当状态很多的时候，给q函数和v函数的每个函数值都独立地存一个表是不现实的。我们往往会选择把v和q写成带参数的函数，函数的参数数量小于状态数量，通过调整函数的参数来匹配观察到的returns。

 

然后是v的一个递归形式

 

上面这个公式是v函数的贝尔曼方程，他表示出了一个状态的V函数和下一个状态的关系。

 

 

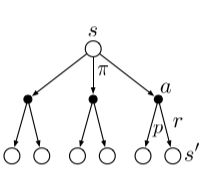
空心圆代表状态，实心圆代表一个state-action pair。

这张图可以和上面的公式很完美地对应起来，从叶子读到树根，就是刚刚的公式。

这种图叫backup diagrams 这是他的定义。

这两道题目挺有趣，可以写一下