集合的伪随机遍历

有时候可能会遇到这样的需求：

1.随机播放歌单里的歌曲，但限定不得与已播放过的歌曲重复 

2.拼图游戏每次重新开始时需要随机初始化碎片的位置，要求随机出的位置不得重复

算法：集合的伪随机遍历

语言：C++

输入：源集合source

输出：一连串不重复的随机数，随机数个数等于source集合元素的个数。

头文件及全局变量：

#include 
#include 
#include 
#include 

int gNum = 26;
char gSource[26] = { 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j',
					'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't',
					'u', 'v', 'w', 'x', 'y', 'z' };
char gResult[26] = {'?'};
std::unordered_set gHashSet;

方案一：第一次通过随机数取得source集合中的元素后，存放到另一个数组(result数组)当中；然后接下来每次取得source集合的元素后与result数组内的元素比较，若有重复则重新取。

void test1()
{
	while (gResult.size() < gNum)
	{
		// temp为找到的一个随机数索引，未校验是否重复
		int temp = rand() % gNum; 
		bool isDifferent = true;

		// 与已得到的随机数校验，一旦出现相同就跳出内循环重新找temp
		for (const char& t : gResult)
		{
			if (gSource[temp] == t)
			{
				isDifferent = false;
				break;
			}
		}

		// 通过校验
		if (isDifferent)
			gResult.push_back(gSource[temp]);
	}

	for (const char& t : gResult)
	{
		std::cout << t;
	}
}

方案二：将source集合中的元素随机地插入到HashSet中，直到HashSize长度等于集合长度。

void test2()
{
	while (gHashSet.size() < gNum)
	{
		int temp = rand() % gNum; 
		gHashSet.insert(gSource[temp]);
	}

	for (const char& t : gHashSet)
	{
		std::cout << t;
	}
}

这两种方法得到数据都有点硬着头皮上的感觉，其实随机遍历就像在跳着走一条直线，从某个元素开始前进x步或者后退y步，最终足迹踩遍整条直线。

void test3()
{
	int prime = 29;
	int skip = 0;
	int nextMember = 0;

	// If the skip value is divisible by the prime number, we will only access
	// index 0, and this is not what we want.
	while (skip%prime == 0)
	{
		int ra = rand() % prime + 1;
		int rb = rand() % prime + 1;
		int rc = rand() % prime + 1;
		skip = ra * gNum * gNum + rb * gNum + rc;   // skip needs 8 bytes' unit "long long" to store it.
	}

	for (int i = 0; i < gNum; ++i)
	{
		do {
			nextMember += skip;
			nextMember %= prime;
		} while (nextMember <= 0 || nextMember > gNum);
		gResult.push_back(gSource[nextMember-1]);
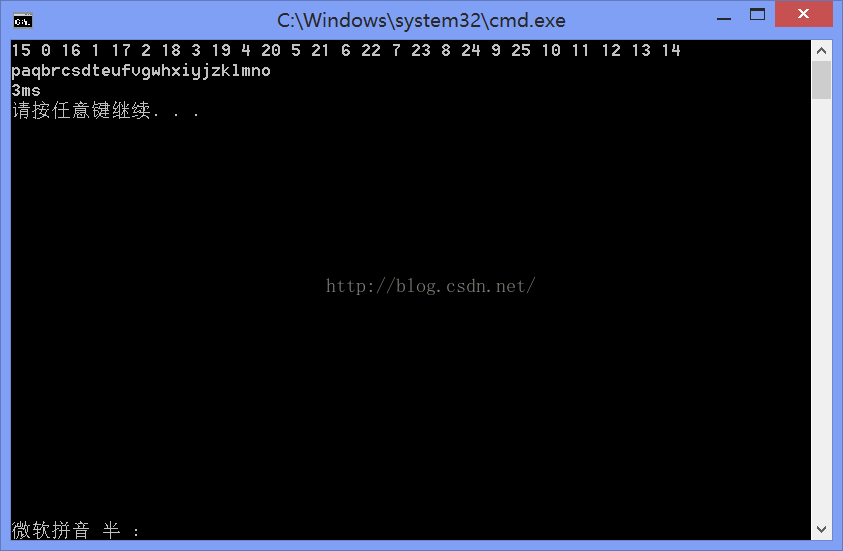
		std::cout << nextMember-1<<" ";
	}

	for (const char& t : gResult)
	{
		std::cout << t;
	}
}

上述算法要注意prime要大于gNum且是素数，如本例取prime为29(gNum=26)，此时再由ra,rb,rc三个随机取得的在1-29以内的数得到skip，要保证skip值可以被prime除尽。

额外输出一下nextNumber-1，即随机获取的source集合索引数。比如，q对应26字母表中第17个字母，source[16].

可以观察到，每个数字之间差值是有规律的(因为nextNumber每次+=skip值后%=prime)：

-12，+17，-12，+5，-12，+17，-12，+17，-12，+17...

可以观察到每次随机取的索引数有一些规律：

1.当数字大于等于12时，每次后退12.

2.当数字小于等于8时，每次前进17.

3.当数字在大于8，小于12时，由于此时前进17会超过最大索引数25，所以前进5.

这样一来，就伪随机地遍历了整个集合，同时其中的规律又可以由自己控制。

比如我们将prime换为31：

显然，此时：后退15，前进16，超过索引时前进1.

那你有可能会觉得这样一来随机数似乎没什么神秘感了，容易被发现规律。

实际上我们可以写一个专门取素数的类PrimeSearch，prime在每次“随机”取完1-n个元素时，

prime = primeSearch.getNextPrime();，然后呢，PrimeSearch内部如何取素数是我们可以提前定义的。

这样一来，就可以定制出满足需求的随机遍历了，较第一、第二种方案更为高级。