详解DDPG（附pytorch代码）

（1）策略网络的更新

为了最大化策略网络输出的动作在值函数网络中的Q值。DDPG的目标是让策略网络输出的动作能够最大化Q值，即 $$\underset{\theta }{\max }{Q}_{\varphi }\left(s,{\mu }_{\theta }(s)\right)$$ 其中 $\theta$ 是策略网络的参数， $\varphi$ 是值函数网络的参数，${\mu }_{\theta }(s)$ 是策略网络输出的动作。为了使用梯度下降法来更新 \theta ，我们需要求出目标函数对 \theta 的梯度，即 ${\nabla }_{\theta }{Q}_{\varphi }\left(s,{\mu }_{\theta }(s)\right)$ 由于Q值是由值函数网络计算的，而不是直接由策略网络输出的，所以我们需要使用链式法则来求出梯度，即 $${\nabla }_{\theta }{Q}_{\varphi }\left(s,{\mu }_{\theta }(s)\right)={\nabla }_a{Q}_{\varphi }\left(s,a\right){\mid }_{a={\mu }_{\theta }(s)}\cdot {\nabla }_{\theta }{\mu }_{\theta }(s)$$ 其中，第一项是Q值对动作的梯度，第二项是策略网络对参数的梯度。为了最大化Q值，我们需要沿着梯度的方向更新参数，即 $\Delta \theta =\alpha {\nabla }_{\theta }{Q}_{\varphi }\left(s,{\mu }_{\theta }(s)\right)$ 其中 \alpha 是学习率。

但是在实际的代码实现中，我们通常使用一个损失函数来表示优化目标，并且使用梯度下降法来最小化损失函数。为了与最大化Q值的目标一致，我们需要将损失函数定义为Q值的负数，即 $$L=-Q_{\varphi }\left(s,{\mu }_{\theta }(s)\right)$$ 这样，损失函数对参数的梯度就是Q值对参数的梯度的负数，即 ${\nabla }_{\theta }L=-{\nabla }_{\theta }{Q}_{\varphi }\left(s,{\mu }_{\theta }(s)\right)$ 那么我们就可以使用梯度下降法来更新参数，即 $\Delta \theta =-\alpha {\nabla }_{\theta }L$ 这样就相当于沿着Q值对参数的梯度的方向更新参数，从而达到最大化Q值的目标。

（2）更新

价值网络更新：

• next_action=target_actor(next_state)
• target_value=target_critic(next_state,next_acion.detach())
• TD_target=reward + (1.0 - done) * self.gamma * target_value
• now_value=critic(state, action)
• value_loss = nn.MSELoss()(now_value, TD_target.detach())

策略网络更新：

• now_actor=actor(state)
• score_now=critic(state, now_actor)
• policy_loss = -score_now.mean()或-torch.mean(now_score)注意有负号

（3）NormalizedActions（代码中的）

NormalizedActions是一个类，它的作用是对连续的动作空间进行归一化，使其范围在[-1, 1]之间1。NormalizedActions是一个gym的ActionWrapper，它可以对任何一个gym环境的动作空间进行包装，从而实现动作空间的归一化。NormalizedActions的主要方法有两个：_action和_reverse_action。_action方法是将原始的动作空间映射到[-1, 1]之间，_reverse_action方法是将归一化后的动作空间还原到原始的范围12。NormalizedActions有什么作用呢？一方面，它可以使得不同的环境具有相同的动作空间范围，方便进行算法的测试和比较。另一方面，它可以使得策略网络的输出更加稳定和可控，避免出现过大或过小的动作值3

（4）详解DDPG和AC算法区别！！！

1.DDPG价值网络的输入是状态s和动作a，输出是对这个动作a的打分； AC算法中价值网络的输入是状态 s，输出是每个动作的价值
2. DDPG 是一个基于 Q-learning 和 Policy gradient 的混合算法，它适用于连续动作空间的问题。AC 是一个基于 Policy gradient 的算法，它适用于离散或连续动作空间的问题。
3. DDPG 的 actor 网络是一个确定性的策略网络，它直接输出一个具体的动作，而不是一个动作的概率分布。AC 的 actor 网络可以是一个确定性的或者随机性的策略网络，根据不同的变种而定。
4. DDPG 是一个 off-policy 算法，它使用经验回放缓冲区来存储和重用历史经验。AC 是一个 on-policy 算法，它只使用当前策略产生的经验来更新网络。

（5）详解DDPG和AC的目标网络

• DDPG的目标网络有两个，一个是用来更新Q函数的，另一个是用来更新策略函数的。Q函数的目标网络是基于下一个状态和下一个动作的Q值，而策略函数的目标网络是基于当前状态的最优动作。这两个目标网络都利用了确定性策略梯度定理，这个定理表明，如果动作空间是连续的，那么最优策略也是确定性的，即对于每个状态，只有一个最优动作。因此，DDPG可以用一个神经网络来近似这个确定性策略，并用另一个神经网络来近似Q函数。DDPG在更新策略时，利用了Q函数对动作的梯度信息，从而避免了对每个动作求Q值的开销。
• DDPG不需要遵循当前的策略来生成数据，是因为它使用了一个目标网络来给出一致的目标值。目标网络是Q网络和策略网络的一个延迟版本，它们的参数定期从原始网络复制过来。这样，即使原始网络的参数在不断变化，目标网络的参数也保持相对稳定，从而减少了目标值的波动。因此，DDPG可以使用任何策略下的数据来更新原始网络，而不会导致不稳定的学习 。
• AC算法中的目标网络只有一个，是用来更新价值函数的，而不是策略函数。价值函数的目标值是基于下一个状态的价值，而不是基于下一个动作的Q值。因此，AC算法中的目标网络并不能解决在连续动作空间上求最大Q值的问题。AC算法需要遵循当前的策略来生成数据，是因为它使用了策略梯度定理，这个定理要求数据的分布与当前的策略一致。如果使用了不同策略下的数据，那么策略梯度定理就不再成立，导致学习失败。

（6）其他

• Pendulum-v1的动作空间是一个连续的一维空间，表示施加在摆杆自由端的扭矩，范围是[-2.0, 2.0]。
• Pendulum-v1的观察空间是一个连续的三维空间，表示摆杆自由端的x-y坐标和角速度，范围分别是[-1.0, 1.0]，[-1.0, 1.0]和[-8.0, 8.0]
  
  
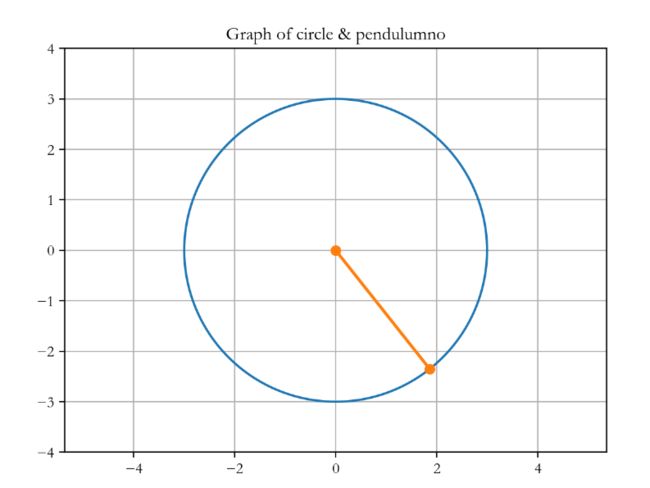
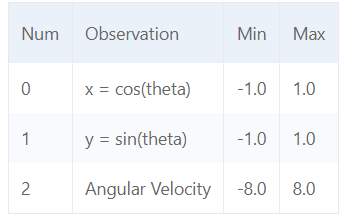
  起始状态是一个在[-pi, pi]的随机角度和一个在[-1,1]的随机角速度。

• 软更新系数0.005;
  高斯噪声标准差0.01
• 策略网络-价值网络（分别对应两个target网络）
• 激活函数最后一层使用的是tanh，调整数值到【-1,1】，然后乘以边界值即可。
• 在演员 (Actor) 网络中，需要输出连续动作;评论家 (Critic) 网络需要将状态和动作拼接起来作为其输入
  来估计Q值，并用Q值来更新演员网络。
• target_update:2
• replay buffer可以放在DDPG对象里面，也可以单独拿出来
• take action函数，记得detach一下action的值

（6）代码

代码参考的一位博主的，忘了链接，侵删！！

import warnings

warnings.filterwarnings("ignore")
import argparse
import datetime
import time
import torch.optim as optim
import torch.nn.functional as F
import gym
from torch import nn

# 这里需要改成自己的RL_Utils.py文件的路径
from s08Nosie_Net.RL_Utils import *


# 将action范围重定在[0,1]之间
class NormalizedActions(gym.ActionWrapper):
    def action(self, action):
        low_bound = self.action_space.low
        upper_bound = self.action_space.high
        action = low_bound + (action + 1.0) * 0.5 * (upper_bound - low_bound)
        action = np.clip(action, low_bound, upper_bound)
        return action

    def reverse_action(self, action):
        low_bound = self.action_space.low
        upper_bound = self.action_space.high
        action = 2 * (action - low_bound) / (upper_bound - low_bound) - 1
        action = np.clip(action, low_bound, upper_bound)
        return action


# Ornstein–Uhlenbeck噪声
'''
 在强化学习中，Ornstein–Uhlenbeck噪声通常被用作探索策略的一种方法，
 因为它可以产生相关的噪声序列，从而使得动作选择更加平滑和连续23。
 '''
class OUNoise(object):
    def __init__(self, action_space, mu=0.0, theta=0.15, max_sigma=0.3, min_sigma=0.3, decay_period=100000):
        self.mu = mu  # OU噪声的参数
        self.theta = theta  # OU噪声的参数
        self.sigma = max_sigma  # OU噪声的参数
        self.max_sigma = max_sigma
        self.min_sigma = min_sigma
        self.decay_period = decay_period
        self.n_actions = action_space.shape[0]
        self.low = action_space.low
        self.high = action_space.high
        self.reset()

    def reset(self):
        self.obs = np.ones(self.n_actions) * self.mu

    def evolve_obs(self):
        x = self.obs
        dx = self.theta * (self.mu - x) + self.sigma * np.random.randn(self.n_actions)
        self.obs = x + dx
        return self.obs

    def get_action(self, action, t=0):
        ou_obs = self.evolve_obs()
        self.sigma = self.max_sigma - (self.max_sigma - self.min_sigma) * min(1.0, t / self.decay_period)  # sigma会逐渐衰减
        return np.clip(action + ou_obs, self.low, self.high)  # 动作加上噪声后进行剪切


# 经验回放对象
class ReplayBuffer:
    def __init__(self, capacity):
        self.capacity = capacity  # 经验回放的容量
        self.buffer = []  # 缓冲区
        self.position = 0

    def push(self, state, action, reward, next_state, done):
        ''' 缓冲区是一个队列，容量超出时去掉开始存入的转移(transition)
        '''
        if len(self.buffer) < self.capacity:
            self.buffer.append(None)
        self.buffer[self.position] = (state, action, reward, next_state, done)
        self.position = (self.position + 1) % self.capacity

    def sample(self, batch_size):
        batch = random.sample(self.buffer, batch_size)  # 随机采出小批量转移
        state, action, reward, next_state, done = zip(*batch)  # 解压成状态，动作等
        return state, action, reward, next_state, done

    def __len__(self):
        ''' 返回当前存储的量
        '''
        return len(self.buffer)


# 演员网络（给定状态，输出动作）
class Actor(nn.Module):
    def __init__(self, n_states, n_actions, hidden_dim, init_w=3e-3):
        super(Actor, self).__init__()
        self.linear1 = nn.Linear(n_states, hidden_dim)
        self.linear2 = nn.Linear(hidden_dim, hidden_dim)
        self.linear3 = nn.Linear(hidden_dim, n_actions)

        self.linear3.weight.data.uniform_(-init_w, init_w)
        self.linear3.bias.data.uniform_(-init_w, init_w)

    def forward(self, x):
        x = F.relu(self.linear1(x))
        x = F.relu(self.linear2(x))
        x = torch.tanh(self.linear3(x))
        return x


# 评论员网络（给定状态-动作对，做出评价）
class Critic(nn.Module):
    def __init__(self, n_states, n_actions, hidden_dim, init_w=3e-3):
        super(Critic, self).__init__()

        self.linear1 = nn.Linear(n_states + n_actions, hidden_dim)
        self.linear2 = nn.Linear(hidden_dim, hidden_dim)
        self.linear3 = nn.Linear(hidden_dim, 1)
        # 随机初始化为较小的值
        self.linear3.weight.data.uniform_(-init_w, init_w)
        self.linear3.bias.data.uniform_(-init_w, init_w)

    def forward(self, state, action):
        # 按维数1拼接
        x = torch.cat([state, action], 1)
        x = F.relu(self.linear1(x))
        x = F.relu(self.linear2(x))
        x = self.linear3(x)
        return x


# 深度确定性策略梯度算法对象
class DDPG:
    def __init__(self, n_states, n_actions, arg_dict):
        self.device = torch.device(arg_dict['device'])
        # DDPG要训练四个网络：Q网络，Q-target网络，策略网络，策略-target网络
        self.critic = Critic(n_states, n_actions, arg_dict['hidden_dim']).to(self.device)
        self.actor = Actor(n_states, n_actions, arg_dict['hidden_dim']).to(self.device)
        self.target_critic = Critic(n_states, n_actions, arg_dict['hidden_dim']).to(self.device)
        self.target_actor = Actor(n_states, n_actions, arg_dict['hidden_dim']).to(self.device)

        # 复制参数到目标网络
        for target_param, param in zip(self.target_critic.parameters(), self.critic.parameters()):
            target_param.data.copy_(param.data)
        for target_param, param in zip(self.target_actor.parameters(), self.actor.parameters()):
            target_param.data.copy_(param.data)

        self.critic_optimizer = optim.Adam(
            self.critic.parameters(), lr=arg_dict['critic_lr'])
        self.actor_optimizer = optim.Adam(self.actor.parameters(), lr=arg_dict['actor_lr'])
        self.memory = ReplayBuffer(arg_dict['memory_capacity'])
        self.batch_size = arg_dict['batch_size']
        self.soft_tau = arg_dict['soft_tau']  # 软更新参数
        self.gamma = arg_dict['gamma']

    def choose_action(self, state):
        state = torch.FloatTensor(state).unsqueeze(0).to(self.device)
        action = self.actor(state)
        return action.detach().cpu().numpy()[0, 0]

    def update(self):
        if len(self.memory) < self.batch_size:  # 当 memory 中不满足一个批量时，不更新策略
            return
        # 从经验回放中(replay memory)中随机采样一个批量的转移(transition)
        state, action, reward, next_state, done = self.memory.sample(self.batch_size)
        # 转变为张量
        state = torch.FloatTensor(np.array(state)).to(self.device)
        next_state = torch.FloatTensor(np.array(next_state)).to(self.device)
        action = torch.FloatTensor(np.array(action)).to(self.device)
        reward = torch.FloatTensor(reward).unsqueeze(1).to(self.device)
        done = torch.FloatTensor(np.float32(done)).unsqueeze(1).to(self.device)

        policy_loss = self.critic(state, self.actor(state))
        policy_loss = -policy_loss.mean()
        next_action = self.target_actor(next_state)
        target_value = self.target_critic(next_state, next_action.detach())
        expected_value = reward + (1.0 - done) * self.gamma * target_value
        expected_value = torch.clamp(expected_value, -np.inf, np.inf)

        value = self.critic(state, action)
        value_loss = nn.MSELoss()(value, expected_value.detach())

        self.actor_optimizer.zero_grad()
        policy_loss.backward()
        self.actor_optimizer.step()
        self.critic_optimizer.zero_grad()
        value_loss.backward()
        self.critic_optimizer.step()
        # 软更新
        for target_param, param in zip(self.target_critic.parameters(), self.critic.parameters()):
            target_param.data.copy_(
                target_param.data * (1.0 - self.soft_tau) +
                param.data * self.soft_tau
            )
        for target_param, param in zip(self.target_actor.parameters(), self.actor.parameters()):
            target_param.data.copy_(
                target_param.data * (1.0 - self.soft_tau) +
                param.data * self.soft_tau
            )

    def save_model(self, path):
        Path(path).mkdir(parents=True, exist_ok=True)
        torch.save(self.actor.state_dict(), path + 'checkpoint.pt')

    def load_model(self, path):
        self.actor.load_state_dict(torch.load(path + 'checkpoint.pt'))

    # 训练函数


def train(arg_dict, env, agent):
    # 开始计时
    startTime = time.time()
    print(f"环境名: {arg_dict['env_name']}, 算法名: {arg_dict['algo_name']}, Device: {arg_dict['device']}")
    print("开始训练智能体......")
    ou_noise = OUNoise(env.action_space)  # noise of action
    rewards = []  # 记录所有回合的奖励
    ma_rewards = []  # 记录所有回合的滑动平均奖励
    for i_ep in range(arg_dict['train_eps']):
        state = env.reset()
        ou_noise.reset()
        done = False
        ep_reward = 0
        i_step = 0
        while not done:
            if arg_dict['train_render']:
                env.render()
            i_step += 1
            action = agent.choose_action(state)
            action = ou_noise.get_action(action, i_step)
            next_state, reward, done, _ = env.step(action)
            ep_reward += reward
            agent.memory.push(state, action, reward, next_state, done)
            agent.update()
            state = next_state
        if (i_ep + 1) % 10 == 0:
            print(f'Env:{i_ep + 1}/{arg_dict["train_eps"]}, Reward:{ep_reward:.2f}')
        rewards.append(ep_reward)
        if ma_rewards:
            ma_rewards.append(0.9 * ma_rewards[-1] + 0.1 * ep_reward)
        else:
            ma_rewards.append(ep_reward)
    print('训练结束 , 用时: ' + str(time.time() - startTime) + " s")
    # 关闭环境
    env.close()
    return {'episodes': range(len(rewards)), 'rewards': rewards, 'ma_rewards': ma_rewards}


# 测试函数
def test(arg_dict, env, agent):
    startTime = time.time()
    print("开始测试智能体......")
    print(f"环境名: {arg_dict['env_name']}, 算法名: {arg_dict['algo_name']}, Device: {arg_dict['device']}")
    rewards = []  # 记录所有回合的奖励
    ma_rewards = []  # 记录所有回合的滑动平均奖励
    for i_ep in range(arg_dict['test_eps']):
        state = env.reset()
        done = False
        ep_reward = 0
        i_step = 0
        while not done:
            if arg_dict['test_render']:
                env.render()
            i_step += 1
            action = agent.choose_action(state)
            next_state, reward, done, _ = env.step(action)
            ep_reward += reward
            state = next_state
        rewards.append(ep_reward)
        if ma_rewards:
            ma_rewards.append(0.9 * ma_rewards[-1] + 0.1 * ep_reward)
        else:
            ma_rewards.append(ep_reward)
        print(f"Epside:{i_ep + 1}/{arg_dict['test_eps']}, Reward:{ep_reward:.1f}")
    print("测试结束 , 用时: " + str(time.time() - startTime) + " s")
    env.close()
    return {'episodes': range(len(rewards)), 'rewards': rewards}


# 创建环境和智能体
def create_env_agent(arg_dict):
    env = NormalizedActions(gym.make(arg_dict['env_name']))  # 装饰action噪声
    env.seed(arg_dict['seed'])  # 随机种子
    n_states = env.observation_space.shape[0]
    n_actions = env.action_space.shape[0]
    agent = DDPG(n_states, n_actions, arg_dict)
    return env, agent

'''
动作：往左转还是往右转，用力矩来衡量，即力乘以力臂。范围[-2,2]
状态：cos(theta), sin(theta) , thetadot（角速度）
奖励：总的来说，越直立拿到的奖励越高，越偏离，奖励越低。
游戏结束：200步后游戏结束。所以要在200步内拿到的分越高越好
'''
if __name__ == '__main__':
    # 防止报错 OMP: Error #15: Initializing libiomp5md.dll, but found libiomp5md.dll already initialized.
    os.environ["KMP_DUPLICATE_LIB_OK"] = "TRUE"
    # 获取当前路径
    curr_path = os.path.dirname(os.path.abspath(__file__))
    # 获取当前时间
    curr_time = datetime.datetime.now().strftime("%Y_%m_%d-%H_%M_%S")
    # 相关参数设置
    parser = argparse.ArgumentParser(description="hyper parameters")
    parser.add_argument('--algo_name', default='DDPG', type=str, help="name of algorithm")
    parser.add_argument('--env_name', default='Pendulum-v1', type=str, help="name of environment")
    parser.add_argument('--train_eps', default=300, type=int, help="episodes of training")
    parser.add_argument('--test_eps', default=20, type=int, help="episodes of testing")
    parser.add_argument('--gamma', default=0.99, type=float, help="discounted factor")
    parser.add_argument('--critic_lr', default=1e-3, type=float, help="learning rate of critic")
    parser.add_argument('--actor_lr', default=1e-4, type=float, help="learning rate of actor")
    parser.add_argument('--memory_capacity', default=8000, type=int, help="memory capacity")
    parser.add_argument('--batch_size', default=128, type=int)
    parser.add_argument('--target_update', default=2, type=int)
    parser.add_argument('--soft_tau', default=1e-2, type=float)
    parser.add_argument('--hidden_dim', default=256, type=int)
    parser.add_argument('--device', default='cuda', type=str, help="cpu or cuda")
    parser.add_argument('--seed', default=520, type=int, help="seed")
    parser.add_argument('--show_fig', default=False, type=bool, help="if show figure or not")
    parser.add_argument('--save_fig', default=True, type=bool, help="if save figure or not")
    parser.add_argument('--train_render', default=False, type=bool,
                        help="Whether to render the environment during training")
    parser.add_argument('--test_render', default=True, type=bool,
                        help="Whether to render the environment during testing")
    args = parser.parse_args()
    default_args = {'result_path': f"{curr_path}/outputs/{args.env_name}/{curr_time}/results/",
                    'model_path': f"{curr_path}/outputs/{args.env_name}/{curr_time}/models/",
                    }
    # 将参数转化为字典 type(dict)
    arg_dict = {**vars(args), **default_args}
    print("算法参数字典:", arg_dict)

    # 创建环境和智能体
    env, agent = create_env_agent(arg_dict)
    # 传入算法参数、环境、智能体，然后开始训练
    res_dic = train(arg_dict, env, agent)
    print("算法返回结果字典:", res_dic)
    # 保存相关信息
    agent.save_model(path=arg_dict['model_path'])
    save_args(arg_dict, path=arg_dict['result_path'])
    save_results(res_dic, tag='train', path=arg_dict['result_path'])
    plot_rewards(res_dic['rewards'], arg_dict, path=arg_dict['result_path'], tag="train")

    # =================================================================================================
    # 创建新环境和智能体用来测试
    print("=" * 300)
    env, agent = create_env_agent(arg_dict)
    # 加载已保存的智能体
    agent.load_model(path=arg_dict['model_path'])
    res_dic = test(arg_dict, env, agent)
    save_results(res_dic, tag='test', path=arg_dict['result_path'])
    plot_rewards(res_dic['rewards'], arg_dict, path=arg_dict['result_path'], tag="test")

（8）OUNoise（Ornstein-Uhlenbeck Noise）

在强化学习中，OUNoise（Ornstein-Uhlenbeck Noise）是一种常用的随机噪声模型，通常用于探索性策略（Exploration Strategy）。它模拟了一个连续时间和自相关性的高斯过程，可以为智能体的动作添加随机性，以促进探索和学习。

OUNoise 的特点是具有自回归性质，即当前噪声值受到过去噪声值的影响。这使得 OUNoise 生成的噪声在一定程度上具有平滑性，避免了剧烈的随机变动。这对于强化学习任务中的连续动作空间非常有用，可以帮助智能体探索更广泛的动作空间。

在强化学习中，OUNoise 常用于确定动作噪声的大小和方向。通过为智能体的动作添加 OUNoise，可以使智能体在训练过程中保持一定的探索性，以便发现更优的策略。随着训练的进行，噪声的强度通常会逐渐减小，使智能体逐渐收敛到最佳策略。

OUNoise 的参数包括：

• mu：OU噪声的均值，通常设置为0。

• theta：OU噪声的自相关时间常数，控制了噪声的平滑性和自回归特性。

• sigma：OU噪声的标准差，控制了噪声的强度。

• max_sigma 和 min_sigma：用于在训练过程中逐渐减小噪声强度的上下限。

• decay_period：噪声强度衰减的时间周期。

通过在训练过程中应用 OUNoise，智能体可以更好地探索环境，增加对未知情况的适应能力，并提高学习的稳定性和收敛速度。在测试阶段，可以选择禁用 OUNoise 或减小噪声的强度，以获得更稳定和确定性的动作输出。

（9）DDPG解决离散动作问题

DDPG（Deep Deterministic Policy Gradient）是一种强化学习算法，通常用于解决连续动作空间的问题。然而，DDPG本身是基于确定性策略的算法，不直接适用于离散动作空间。但是，可以通过一些技巧将DDPG算法扩展到离散动作问题上。
下面是一种常见的方法，称为混合策略（Hybrid Policy）：

• 离散动作空间的表示：将离散动作空间离散化为一组有限的离散动作。可以通过将连续动作空间分成离散的区域，或者使用动作索引来表示离散动作。

• 值函数网络：使用一个值函数网络（Q-network）来估计离散动作状态对的值函数。这个网络接受状态作为输入，并输出每个离散动作的值。

• 策略网络：使用一个策略网络（Actor-network）来学习选择离散动作的策略。策略网络接受状态作为输入，并输出每个离散动作的概率分布。

• 混合策略更新：在训练过程中，使用DDPG的经验回放和梯度更新方法来更新值函数网络和策略网络。值函数网络用于估计动作值，策略网络用于选择动作。

有篇论文(Cooperative Caching and Beamforming for CoMP-Enabled Mobile Edge Networks)示例：

• 本文为了将DDPG算法应用于离散动作空间，采用了一种混合编码的方法，即将离散动作转化为连续动作。具体地，本文将每个内容的缓存决策编码为一个0-1向量，其中1表示缓存该内容，0表示不缓存该内容。然后，本文将这个0-1向量转化为一个实数向量，其中每个元素的值介于0和1之间，表示缓存该内容的概率。这样，本文就可以用DDPG算法输出一个实数向量作为内容缓存决策。其中策略网络的输出层是一个全连接层，激活函数是sigmoid函数，可以输出介于0和1之间的实数值。在执行决策时，本文再将这个实数向量转化为一个0-1向量，根据每个元素的值与一个随机数的大小关系，确定是否缓存该内容。
• 也就是说，输出结果小于0.5就取值为0，大于0.5就取值为1。

还有篇论文（Collaborative Edge Caching and Transcoding for 360◦ Video Streaming Based on Deep Reinforcement Learning）：

• 本文的缓存替换动作空间是指每个边缘服务器需要选择一个切片来替换，而每个切片都有一个固定的索引，从1到M，其中M是切片的总数1。

• 本文使用DDPG来处理缓存替换动作空间时，将每个切片的索引用一个连续的数值来表示，即将[1,M]映射到[0,1]，并用一个线性层作为输出层1。

• 本文在执行缓存替换动作时，将输出层的数值再映射回[1,M]，并取整，得到对应的切片索引1。