20200521模拟赛A. island（笛卡尔树||分治+分类讨论计数）
题解：
毒瘤分类讨论题
我们先把所有格子纵向互相走的总贡献
直接记录一下前缀和就O(n)了
设F1(x)表示
设F2(x)表示
然后再把跨过0号点的路径的贡献算出来
![2*((\sum_{i=1}^nF1(-L[i]-1))*(\sum_{i=1}^n-L[i])+(\sum_{i=1}^nF1(R[i]))*(\sum_{i=1}^nR[i]))](http://img.e-com-net.com/image/info8/64369af74ac947eb8426a5bb2f8180ab.gif)
（这里的L[i]是负的）
然后我们需要做的就是计算左边走到左边，右边走到右边的贡献了
这里我们采取分治
为了方便我们把图旋转90°
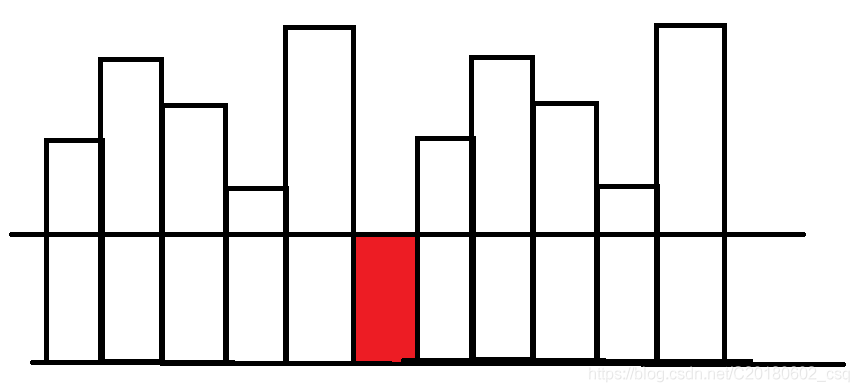
考虑一个区间 [ l , r ] 的最小值A[x]
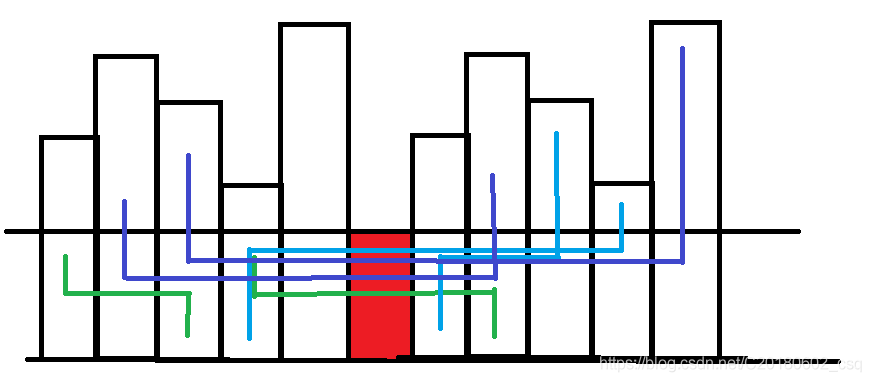
我们对于这个最小值，它需要统计的路径有三种类型
1、下边到下边的贡献（绿色线）
2、上到下以及下到上的贡献（蓝色线）
3、左上到右上+右上到左上的贡献（紫色线）
我们可以分别列出式子
1、下到下
由于我们已经算过了横向的贡献，所有我们只需要考虑纵向贡献
![(F2(A[x])-F1(A[x]))*(r-l+1)^2](http://img.e-com-net.com/image/info8/ff49abfead934c04a4832611776918dc.gif){kind=small}
一个1*A[x]的小矩形块中所有路径的贡献 * 选择两个小矩形的方案数
2、下到上+上到下
下到上:
我们先计算下方的起点（绿点）走到A[x]高度的贡献和
![(r-l+1)*F1(A[x]-1)](http://img.e-com-net.com/image/info8/19ba488462b84ed59f49f1444b8dfbda.gif){kind=small}
（小矩形的个数 * 每一个小矩形的贡献）
然后下方每一个点都要走到上方的每一个点（蓝点）
设cnt(l,r,x)表示，区间[l,r]中高于x的格子有多少个，这个可以预处理前缀和来快速计算（因为x为l,r中的最小值）
![cnt(l,r,x)=sum1[r]-sum1[l-1]-A[x]*(r-l+1)](http://img.e-com-net.com/image/info8/d289cb9926f742ac9653848bcd38da68.gif){kind=small}
所以每一个起点都要到达cnt(l,r,x)个终点，所以每一个起点走到A[x]的贡献和为
![(r-l+1)*F1(A[x]-1)*cnt(l,r,A[x])](http://img.e-com-net.com/image/info8/0d13579fcb5d4df9b94aa3e512e49106.gif){kind=small}
上到下:
同样的道理，我们计算上方终点倒着走走到A[x]的贡献和
我们把
![\sum_{i=l}^rF1(A[i]-x)](http://img.e-com-net.com/image/info8/7b57fbb10ddf4b2399c8cf9d22a7ceab.gif)
，计作F(l,r,x)
我们把式子展开一下
![\sum_{i=l}^r\frac{(A[i]-x)*(A[i]-x+1)}{2}](http://img.e-com-net.com/image/info8/ad4384cef1504ce3a3c1112f0052679f.gif)
![\frac{1}{2}\sum_{i=l}^r(A[i]-x)^2+(A[i]-x)](http://img.e-com-net.com/image/info8/a8152f04097e47e9b17ea0f9f1d92d04.gif)
![\frac{1}{2}\sum_{i=l}^rA[i]^2-2xA[i]+x^2+A[i]-x](http://img.e-com-net.com/image/info8/7b8e341932604f9f901593456f697536.gif)
![\frac{1}{2}\sum_{i=l}^rA[i]^2+(1-2x)A[i]+x(x-1)](http://img.e-com-net.com/image/info8/b4b4e6d340034a918d623b69060d2328.gif)
发现我们只需要记录一下A[i]^2与A[i]的前缀和sum2[i],sum1[i]即可
![\frac{1}{2}(sum2[r]-sum2[l-1]+(1-2x)(sum1[r]-sum1[l-1])+(r-l+1)x(x-1))](http://img.e-com-net.com/image/info8/e2fb268ece5b454eabb1b113b999300d.gif){kind=small}
有由于我们每一个上方的点都倒着走到(r-l+1)*A[x]个下方的点
所以这一部分的贡献就为
![(r-l+1)*A[x]*F(l,r,A[x])](http://img.e-com-net.com/image/info8/614652822be547e3bf0c15a95b9bb8af.gif){kind=small}
总贡献就是把这两个部分的贡献加起来乘个2
3、左上到右上+右上到左上
这一部分就是（左上部分到A[x]的路径长度总贡献*右上部分的总点数
再加上右上部分到A[x]的路径长度总贡献*左上部分的总点数）* 2
表达出来就是
![F(l,x-1,A[x])*cnt(x+1,r,A[x])+F(x+1,r,A[x])*cnt(l,x-1,A[x])](http://img.e-com-net.com/image/info8/510b1fc58de44551ac93199414d93f14.gif){kind=small}
* 2
这样就算完了
分治之后有一个小细节
在计算1、2部分的贡献的时候由于与A[x]以下部分的点有关，而A[x]以下的点有一部分在上一次分治已经算过了
所以还要记录一下上一次分治的A[x']
代码：（区间最小值的位置查询应该是可以用笛卡尔树的，但是作者并不会笛卡尔树，于是就写了ST表）
#include
#include
#include
//#include
using namespace std;
inline int gi()
{
char c;int num=0,flg=1;
while((c=getchar())<'0'||c>'9')if(c=='-')flg=-1;
while(c>='0'&&c<='9'){num=num*10+c-48;c=getchar();}
return num*flg;
}
#define N 1000005
#define LOG 20
const int mod=998244353;
const int inv2=499122177;
const int inv6=166374059;
int n,L[N],R[N],A[N],ans;
int F1(int n)
{
return 1ll*n*(n+1)/2%mod;
}
int F2(int n)
{
return 1ll*n*(n+1)%mod*(2*n+1)%mod*inv6%mod;
}
int sum1[N],sum2[N];
int st[LOG][N],lg[N];
int getmin(int l,int r)
{
int k=lg[r-l+1];
return A[st[k][l]]r) return 0;
return 1ll*(sum2[r]-sum2[l-1]+1ll*(1-2*x)*(sum1[r]-sum1[l-1])+1ll*x*(x-1)%mod*(r-l+1))%mod*inv2%mod;
}
void solve(int l,int r,int pre)
{
if(l>r) return;
int len=r-l+1,x=getmin(l,r);
int cntl=(sum1[x]-sum1[l-1]-1ll*A[x]*(x-l+1))%mod;
int cntr=(sum1[r]-sum1[x]-1ll*A[x]*(r-x))%mod;
ans=(ans+1ll*(F2(A[x]-pre)-F1(A[x]-pre))*len%mod*len)%mod;
ans=(ans+2*(1ll*F1(A[x]-pre-1)*len%mod*(cntl+cntr)+1ll*(A[x]-pre)*len%mod*F(l,r,A[x])))%mod;
ans=(ans+2*(1ll*F(l,x-1,A[x])*cntr+1ll*F(x+1,r,A[x])*cntl))%mod;
solve(l,x-1,A[x]);solve(x+1,r,A[x]);
}
void work(int B[])
{
int i,j,t;
memcpy(A,B,sizeof(A));
for(i=1;i<=n;i++){
sum1[i]=(sum1[i-1]+A[i])%mod;
sum2[i]=(sum2[i-1]+1ll*A[i]*A[i])%mod;
}
lg[0]=-1;
for(i=1;i<=n;i++)lg[i]=lg[i>>1]+1,st[0][i]=i;
//double c1=clock();
for(j=1;j
常数极大。。。其实复杂度也不对，O(nlogn)
然而同一份代码换了C++ -O2的语言之后会快一倍