决策树-预测隐形眼镜类型 （ID3算法，C4.5算法，CART算法，GINI指数,剪枝，随机森林）...

1.

1、问题的引入

2、一个实例

3、基本概念

4、ID3

5、C4.5

6、CART

7、随机森林

2.

我们应该设计什么的算法，使得计算机对贷款申请人员的申请信息自动进行分类，以决定能否贷款?

 

 

一个女孩的母亲要给这个女孩介绍男朋友，于是有了下面的对话：

女儿：多大年纪了？

母亲：26。

女儿：长的帅不帅？

母亲：挺帅的。

女儿：收入高不？

母亲：不算很高，中等情况。

女儿：是公务员不？

母亲：是，在税务局上班呢。

女儿：那好，我去见见。

决策过程：

 

这个女孩的决策过程就是典型的分类树决策。相当于通过年龄、长相、收入和是否公务员对将男人分为两个类别：见和不见

3.定义：

决策树是一种描述对样本实例(男人)进行分类(见或不见)的树形结构。

决策树由结点和有向边组成。最上部是根节点，此时所有样本都在一起，经过该节点后样本被划分到各子节点中。每个子节点再用新的特征来进一步决策，直到最后的叶节点。叶节点上只包含单纯一类样本(见或不见)，不需要在进行划分。

结点两种类型:内部结点和叶结点。

内部结点表示一个特征或属性，叶节点表示一个类。

4.熵

特征选择

首先，我们该选择什么标准(属性、特征)作为我们的首要条件(根节点)对样本(男人)进行划分，决定见或不见呢？——特征选择

母亲希望女儿能最快速的有一个明确的态度，决定见或不见，这样好给男方一个明确的答复。

母亲需要获得尽可能多的信息，减少不确定性。

信息的如何度量？——熵

母亲得到信息越多，女儿的态度越明确，与男方见与不见的不确定性越低。因此，信息量与不确定性相对应。使用熵来表示不确定性的度量。

熵定义：如果一件事有k种可的结果，每种结果的概率为

则我们对此事件的结果进行观察后得到的信息量为:

熵越大，随机变量(见与不见)的不确定性越大。

 

5.条件熵(局部，现象发生的前提下的熵)

条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性。例如，知道男生年龄的前提条件下，根据女儿见与不见的不确定性。

熵与条件熵中概率由数据估计得到时，所对应的熵和条件熵称为经验熵和经验条件熵。若概率为0，令0log0=0

6.信息增益

信息增益表示得知特征X(年龄)的信息使得类Y(见与不见)的信息的不确定性减少程度。

特征A对训练数据集D的信息增益g(D,A)，定义为集合D的经验熵H(D)与特征A给定条件下的经验条件熵H(D|A)之差

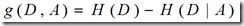
熵H(Y)与条件熵H(Y|X)之差称为互信息，即g(D,A)。

信息增益大表明信息增多，信息增多，则不确定性就越小，母亲应该选择使得信息增益增大的条件询问女儿。

 

7.信息增益准则的特征选择方法

对数据集D，计算每个特征的信息增益，并比较他们的大小，选择信息增益最大的特征。

8.贷款申请样本数据表 （例子）

根据贷款申请样本数据表，我们有15条样本记录，则样本容量为15。最终分为是否贷款2个类，其中是有9条记录，否有6条记录。有年龄、有工作、有自己的房子和信贷情况4个不同特征。每个特征有不同的取值，如年龄有老、中、青3种取值。

熵的定义

计算经验熵

然后计算各特征对数据集D的信息增益。分别以A1，A2，A3，A4表示年龄、有工作、有自己的房子和信贷情况4个特征。

根据年龄有取值青年、中年、老年。

青年贷款是2条记录，否3条记录，共5条记录

中年贷款是3条记录，否2条记录，共5条记录

老年贷款是4条记录，否1条记录，共5条记录

条件熵公式

 

条件熵公式

年龄为已知条件的条件熵为

D1，D2，D3分别是年龄取值为青年、中年、老年的样本子集。

以年龄为条件的信息增益为

有工作的信息增益

有房子的信息增益

信贷情况的信息增益

最后比较各特征的信息增益值，对于特征A3有自己房子的信息增益值最大，所以选择特征A3作为最优特征。

结合最开始的例子，我们可以知道年龄作为首选特征的信息增益最大，选择年龄作为见与不见首要条件。

9.ID3算法

ID3算法的核心是在决策树各个子节点上应用信息增益准则选择特征，递归的构建决策树，具体方法是:从根节点开始，对节点计算所有可能的特征的信息增益，选择信息增益最大的特征作为节点的特征，由该特征的不同取值建立子节点；再对子节点递归调用以上方法，构建决策树。

直到所有特征的信息增益均很小或没有特征可以选择为止。最后得到一个决策树。

 

    继续前面的过程，由于特征A3(有自己房子)的信息增益值最大，所以选择特征A3作为根节点的特征。它将训练数据集划分为两个子集D1(A3取值为是)和D2(A3取值为否)。由于D1只有同一类样本点，可以明确要贷款给D1，所以它成为一个叶节点，节点类标记为“是”。

对于D2则需要从特征A1(年龄)，A2(有工作)和A4(信贷情况)中选择新的特征。计算各个特征的信息增益:

 

选择信息增益最大的特征A2(有工作)作为节点特征。A2有2个取值，一个对应“是”(有工作)的子节点，包含3个样本，他们属于同一类，所以这是一个叶节点，类标记为“是”；另一个对应“否”(无工作)的子节点，包含6个样本，属于同一类，这也是一个叶节点，类标记为“否”。

换句话有15个贷款人，经过是否有房这一筛选条件，有房子的6个人能够贷款。剩余9个人需要进一步筛选，以是否有工作为筛选条件，有工作的3个人可以贷款，无工作的6个人不能够贷款。

该决策树只用了两个特征(有两个内部结点)，以有自己的房子作为首要判决条件，然后以有工作作为判决条件是否可以贷款。

ID3算法只有树的生成，所以该算法生成的树容易产生过拟合，分得太细，考虑条件太多。

10.C4.5算法

1.用信息增益选择属性时偏向于选择分枝比较多的属性值，即取值 多的属性。

2.不能处理连续属性。

信息增益比定义:特征A对训练数据集D的信息增益比定义为其信息增益与训练数据D关于特征A的值的熵HA(D)之比

其中， ，n是特征A取值个数。如A代表年龄。

C4.5算法的改进

C4.5算法是数据挖掘十大算法之一，它是对ID3算法的改进，相对于ID3算法主要有以下几个改进

（1）用信息增益比来选择属性

（2）在决策树的构造过程中对树进行剪枝

（3）对非离散数据也能处理

（4）能够对不完整数据进行处理

11.CART算法

分类回归树(CART,Classification And Regression Tree)其核心思想与ID3和C4.5相同，主要的不同处在于CART在每一个节点上都采用二分法，即每个节点都只能有两个子节点，最后构成的是二叉树。

划分方法

剪枝

名称	体温	表面覆盖	胎生	产蛋	能飞	水生	有腿	冬眠	类标记
人	恒温	毛发	是	否	否	否	是	否	哺乳类
巨蟒	冷血	鳞片	否	是	否	否	否	是	爬行类
鲑鱼	冷血	鳞片	否	是	否	是	否	否	鱼类
鲸	恒温	毛发	是	否	否	是	否	否	哺乳类
蛙	冷血	无	否	是	否	有时	是	是	两栖类
巨蜥	冷血	鳞片	否	是	否	否	是	否	爬行类
蝙蝠	恒温	毛发	是	否	是	否	是	否	哺乳类
猫	恒温	皮	是	否	否	否	是	否	哺乳类
豹纹鲨	冷血	鳞片	是	否	否	是	否	否	鱼类
海龟	冷血	鳞片	否	是	否	有时	是	否	爬行类
豪猪	恒温	刚毛	是	否	否	否	是	是	哺乳类
鳗	冷血	鳞片	否	是	否	是	否	否	鱼类
蝾螈	冷血	无	否	是	否	有时	是	是	两栖类

上例是属性有8个，每个属性又有多个离散的值可取。在决策树的每一个节点上我们可以按任一个属性的任一个值进行划分。比如最开始我们按：

1）表面覆盖为毛发和非毛发

2）表面覆盖为鳞片和非鳞片

3）体温为恒温和非恒温

要产生树的左右两个孩子，按哪种划分最好呢？一般我们采用GINI指数，作为划分标准。总体内包含的类别越杂乱，GINI指数就越大（跟熵的概念很相似）

 

12.GINI指数

分类问题中，假设有k个类，样本点属于第i类的概率为pi，则基尼指数定义为

体温为恒温时包含哺乳类5个、鸟类2个，体温为非恒温时包含爬行类3个、鱼类3个、两栖类2个。

体温为恒温时包含哺乳类5个、鸟类2个，则：

体温为非恒温时包含爬行类3个、鱼类3个、两栖类2个,则：

 

集合的基尼指数

如果样本集合D根据特征A是否取某一可能值a被分割成D1和D2两部分，则在特征A的条件下，集合D的基尼增益定义为

如果按照“体温为恒温和非恒温”进行划分的话，我们得到GINI的增益：

集合的基尼指数表示集合D的不确定性，基尼指数值越大，样本属于某类的不确定性也就越大，这点与熵相似。我们总希望获得更多信息，减少不确定性。因此，最好的选取特征划分就是使得集合的基尼指数GINI最小的划分。

13.剪枝

当CART树划分得太细时，会对噪声数据产生过拟合作用。因此我们要通过剪枝来解决。剪枝又分为前剪枝和后剪枝。

前剪枝是指在构造树的过程中就知道哪些节点可以剪掉，于是干脆不对这些节点进行分裂。

后剪枝是指构造出完整的决策树之后再来考查哪些子树可以剪掉。

CART剪枝算法从“完全生长”的决策树的底端剪去一些子树，使决策树变小(模型变简单)，从而能够对未知数据有更准确的预测。

CART剪枝算法由两步组成：首先从生成算法产生的决策树T0底端开始不断剪枝，直到T0的根节点，形成一个子树序列 ；然后通过交叉验证法在独立的验证数据集上对子树序列进行测试，从中选择最优子树。

CART树中的每一个非叶子节点的表面误差率增益值α(误差增加的速率，越小越好)

 

是是子树中包含的叶子节点个数。

是节点t的误差代价，如果该节点被剪枝：

r(t)是节点t的误差率；

p(t)是节点t上的数据占所有数据的比例；

是子树Tt的误差代价，如果该节点不被剪枝。它等于子树Tt上所有叶子节点的误差代价之和。

有个非叶子节点t4如图所示：

已知所有的数据总共有60条，则节点t4的节点误差代价为：

注意:叶子节点的类定义为覆盖的样本占多数的类，即分正确的为多数，分错的为少数。

子树误差代价为：

以t4为根节点的子树上叶子节点有3个，最终：

找到α值最小的非叶子节点，令其左右孩子为空，即该节点成为叶子节点，即剪枝。

14.随机森林

随机森林就是建立很多决策树，组成一个决策树的“森林”，通过多棵树投票来进行决策。这种方法能够有效地提高对新样本的分类准确度。

随机森林的步骤：

首先，对样本数据进行有放回的抽样，得到多个样本集。具体来讲就是每次从原来的N个训练样本中有放回地随机抽取N个样本(包括可能重复样本)。

然后，从候选的特征中随机抽取m个特征，作为当前节点下决策的备选特征，从这些特征中选择最好地划分训练样本的特征。用每个样本集作为训练样本构造决策树。单个决策树在产生样本集和确定特征后，使用CART算法计算，不剪枝。

最后，得到所需数目的决策树后，随机森林方法对这些树的输出进行投票，以得票最多的类作为随机森林的决策。

随机森林的方法即对训练样本进行了采样，又对特征进行了采样，充分保证了所构建的每个树之间的独立性，使得投票结果更准确。

随机森林的随机性体现在每棵树的训练样本是随机的，树中每个节点的分裂属性也是随机选择的。有了这2个随机因素，即使每棵决策树没有进行剪枝，随机森林也不会产生过拟合的现象。

随机森林中有两个可控制参数：森林中树的数量（一般选取值较大）和抽取的属性值m的大小。

随机森林的优点：

（1）分类结果更加准确

（2）可以处理高维度的属性，并且不用做特征选择

（3）即使有很大部分数据遗失，仍可以维持高准确度

（4）学习过程快速

（5）在训练完成后，能够给出哪些属性比较重要

（6）容易实现并行化计算

（7）在训练

15.代码—实现ID3算法

1、准备训练数据

2、计算信息增益

下边是计算

下边计算

3、递归构建决策树

其中当所有的特征都用完时，采用多数表决的方法来决定该叶子节点的分类，即该叶节点中属于某一类最多的样本数，那么我们就说该叶节点属于那一类！

创建树

运行测试：

4、查看生成的决策树

5、测试数据

6、决策树的存储

构造决策树是一个很耗时的任务。为了节省计算时间，最好能够在每次执行分类时调用已经构造好的决策树。为了解决这个问题，需要使用python模块pickle序列化对象，序列化对象可以在磁盘上保存对象，并在需要的时候读取出来。

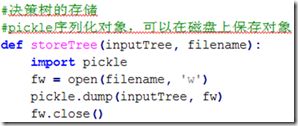
运行测试：

7、示例：使用决策树预测隐形眼镜类型

总结

转载于:https://www.cnblogs.com/chaoren399/p/4847462.html