机器学习决策树:sklearn分类和回归
上面的蓝字关注我们!![]()
作者:alg-flody
编辑:Emily
昨天的推送机器学习:对决策树剪枝,分析了决策树需要剪枝,今天再就这个话题,借助 sklearn 进一步分析决策树分类和回归时过拟合发生后,该如何解决的问题。
上周推送的机器学习:谈谈决策树,介绍了利用逻辑回归算法,二分类一个拥有2个特征的数据集,模拟的结果如下所示:
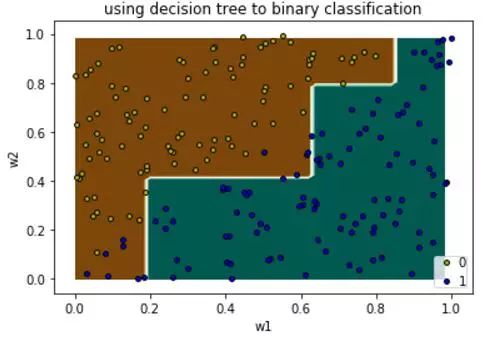
从结果中可以看出,逻辑回归的分类效果是不错的,那么我们尝试用决策树分类这个数据集,看看效果是怎么样的。
通过上图分类的结果,黄色点为0类,相应的它们所在的区域为淡黄色区域,蓝色点为1类,相应的区域为右下区域。得到上图的代码:
def decisionTreeBoundary(data,n_classes=2,plot_colors = "yb",plot_step = 0.02):
#特征的列index
pairidx,pair = [1,2],[1,2]
X = data[:,[1,2]]
y = data[:,3]
# Train
#构造的无参数构造函数
clf = tree.DecisionTreeClassifier()
clf.fit(X, y)
# 绘制决策边界
x_min, x_max = X[:, 0].min(), X[:, 0].max()
y_min, y_max = X[:, 1].min(), X[:, 1].max()
xx, yy = np.meshgrid(np.arange(x_min, x_max, plot_step),
np.arange(y_min, y_max, plot_step))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
cs = plt.contourf(xx, yy, Z, cmap=plt.cm.BrBG)
# 绘制训练点
for i, color in zip(range(n_classes), plot_colors):
idx = np.where(y == i)
clabel=np.array(i,dtype=np.str)
plt.scatter(X[idx, 0], X[idx, 1], c=color,label = clabel,
cmap=plt.cm.RdYlBu, edgecolor='black', s=15)
plt.legend(loc='lower right', borderpad=0, handletextpad=0)
plt.axis("tight")
plt.xlabel("w1")
plt.ylabel("w2")
plt.title("using decision tree to binary classification")
plt.show()
比较决策树和逻辑回归得到的决策边界:
-
逻辑回归得到的决策边界更直接简洁,相应的泛化能力更好些。
-
决策树得到的边界弯弯曲曲,好像被切了很多刀,泛化能力没有逻辑回归好。
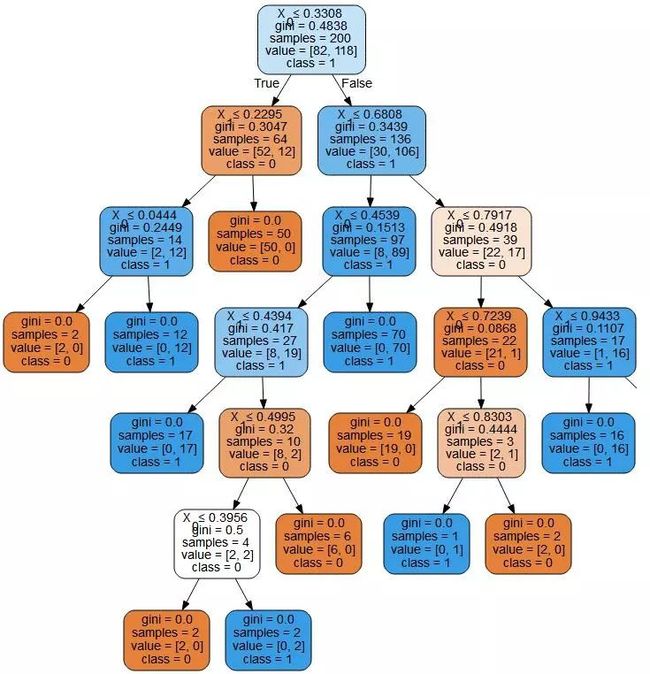
可视化下决策树,
可以看到,决策树的枝枝叶叶有点茂盛,做一下剪枝操作。因此,让我们看下对未经剪枝的决策树,进行剪枝操作后,得到的决策边界是不是会好些,设置每个分裂点的最小样本数不能小于10,clf = tree.DecisionTreeClassifier(max_depth=3)
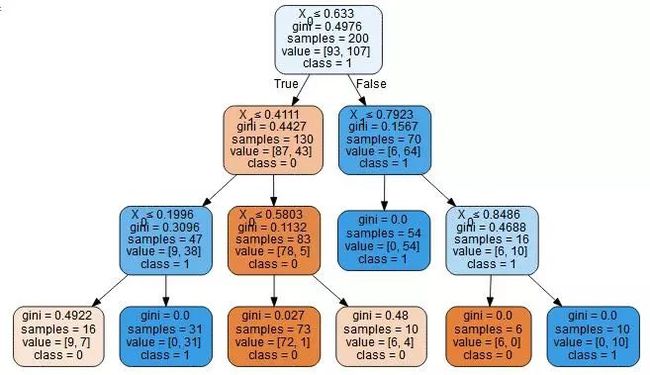
得到的分类边界切分了5刀,过拟合减轻了一些,在训练集上可以看到有些蓝点被错误地分类了,中间部位区域划分的不够合理。
同时可以可视化出对应的决策树深度为3层,共切分了6段。
由以上论述在样本数较少的情况下,可以看到逻辑分类的效果更满意一些,泛化能力可能更好些,决策树很容易过拟合,并且想要减轻过拟合时,准确率上又难以保证。
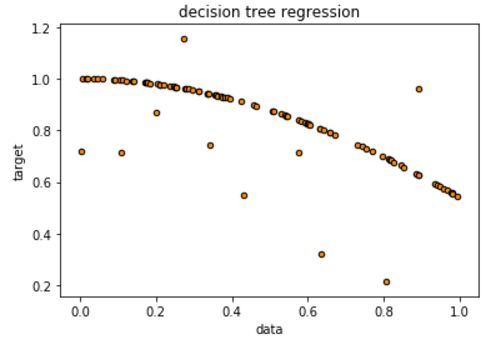
我们首先生成一些需要模拟的数据,可以看到大部分的点(一维,只有一个特征)都位于一条曲线附件,但是有10个噪音点,偏离比较大。
生成这部分点的代码如下所示:
import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt
# Create a random dataset
rng = np.random.RandomState(100)
X = np.sort(rng.rand(100, 1), axis=0)
y = np.cos(X).ravel()
y[::10] += (0.5 - rng.rand(10))
# Plot the results
plt.scatter(X, y, s=20, edgecolor="black",
c="darkorange", label="data")
plt.scatter(X,y)
plt.show()
下面看下直接调用sklearn的API之决策树回归,得到的结果是怎样的。
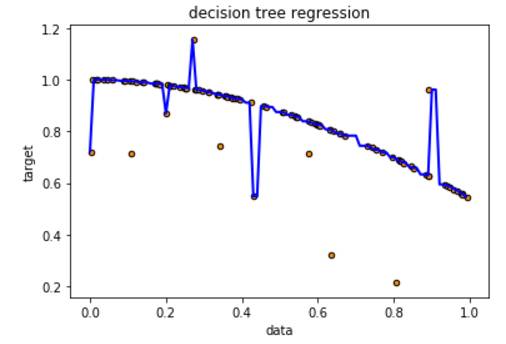
首先不设置树的最大深度,这样决策树在做回归的时候会考虑所有的样本点,而发生过拟合,如下图所示,噪音点也被纳入到了回归曲线上,这是不好的,考虑对决策树进行剪枝,降低过拟合风险。
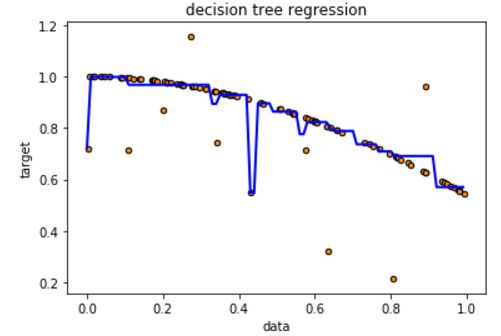
取树的最大深度等于5,看下模拟结果,部分降低了过拟合,但是还是考虑了某些噪音点,考虑继续减小树的深度,
取树的最大深度等于2时的模拟结果,可以看到所有噪音点都被排除在外,不再过拟合。
因此在做决策树回归时,和分类一样,也要考虑过拟合的问题,如果发生过拟合,一般通过调整决策树的超参数来降低过拟合。上面模拟用到的代码如下:
# Import the necessary modules and libraries
def dtr(maxdepth=2):
import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt
# Create a random dataset
rng = np.random.RandomState(100)
X = np.sort(rng.rand(100, 1), axis=0)
y = np.cos(X).ravel()
y[::10] += (0.5 - rng.rand(10))
# Fit regression model
regr = DecisionTreeRegressor(max_depth=5)
regr.fit(X, y)
# Predict
X_test = np.arange(0.0, 1.0, 0.01)[:, np.newaxis]
y_predict = regr.predict(X_test)
# Plot the results
plt.scatter(X, y, s=20, edgecolor="black",
c="darkorange", label="data")
plt.plot(X_test, y_predict, color="blue", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("decision tree regression")
plt.show()
以上分析可以看出,决策树不仅可以做分类,还可以做回归。但是不管做分类还是回归,决策树都要考虑的问题是可能的过拟合发生,如果一旦出现,要考虑通过树的常见的超参数来降低,通常这些超参数包括:
1. criterion gini or entropy,选择哪个特征作为分裂点的判断公式。
2. splitter best or random:选择spitter best的话,是说从所有特征中找最好的切分点, random在数据量大的时候,特征多的时候,在部分特征中找最好的切分点。
3. max_features or None :max_features < 50是一般选择None,即使用所有的特征。
4. max_depth: 树的最大深度
5. min_samples_split:如果节点的样本数小于min_samples_split,则不再对这个节点分裂,这个值是在样本数很大时才用的。
6. min_samples_leaf:叶子节点的样本少于min_samples_leaf,则它和它的兄弟都会被裁剪。
7. max_leaf_nodes:决策树最大的叶子节点数,如果叶子节点大于max_leaf_nodes,则可能发生过拟合了,考虑调小这个值。
8. min_weight_fraction_leaf:这个值限制了叶子节点所有样本权重和的最小值,则会和兄弟节点一起被裁剪。
9. class_weight:调整某个类别的权重,主要考虑到某个类别的样本数所占比例大,导致偏向它,用户可以配置使这个类别权重小一些。
通过调整这些超参数,会得到最优化的结果。
决策树用于分类的优点如上文所述,我们可以解释它,比如在某个特征取值小于多少的时候,它一分为二了哪两个类,这些我们可以通过graphviz模块可视化地观察到,而不像复杂的神经元网络那样,只能得到参数,而无法解释每个参数为什么取这个值。
好了,这三天笔记了决策树的一些基本理论:特征选取方法,如何防止过拟合的发生,以及sklearn中的API直接调用模拟了决策树的分类和回归。
接下来,是否准备自己手动编写一个决策树分类器和回归器,进一步加深对决策树CART算法的理解。
谢谢您的阅读!
交流思想,注重分析,看重过程,包含但不限于:经典算法,机器学习,深度学习,LeetCode 题解,Kaggle 实战,英语沙龙,定期邀请专家发推。期待您的到来!