DirectX11学习笔记十一 法线映射

回顾光照公式

前面学的局部光照里用到了与法线有关的计算公式，也就是漫反射，以点光源为例回顾一下：

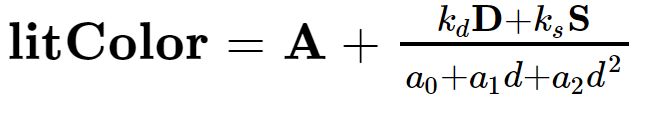
其中 漫反射光D = 漫反射材质系数 点乘 （入射光反方向 点乘 法向量） 点乘 入射光颜色，如下图所示

镜面高光S = 镜面高光材质系数 点乘 （出射光向量 点乘 顶点或像素到摄像机向量）^高光系数 点乘 入射光颜色，如下图所示：

之前计算光照用到的法线都是网格上根据三角形两条边叉乘得到的，但这样的缺点是相邻像素插值得到的法线之间变化非常小，导致整个plane看起来像一个光滑的平面，如果能为texture的每一个像素都提前规定一个法线，就可以表现出平面上凹凸不平的光照现象。

法线纹理

办法就是用一张图片存储法线信息，在渲染时两张图都采样，一张为texture纹理，一张为normal纹理，光照公式不需要动，只需要处理法线。
而法线纹理分Object-space和Tangent-space两种。

前者(左边)颜色信息代表模型空间，后者为切线空间，数据范围[0,1]，通过rgb*2-1来扩大值域范围到[-1,1]。
具体的含义就是，模型空间下的法线纹理，与模型本身密切相关；举个例子，比如有一面竖着的墙(plane)，其模型空间下的法线纹理大多朝向-z轴(对着摄像机)，而墙的网格本身也是正面对着摄像机，那么法线经过采样并做model变换后，渲染出来的结果就是正确的。However, 如果我又找了一个地板的模型，想套用墙的法线纹理，但是地板的网格法线在模型空间下的的朝向是+y，而墙的法线纹理还是超向-z，那么两者的方向就会不一致，渲染的结果就错了。可以理解为，模型空间下的法线纹理只能跟特定的网格配合渲染。

而切线空间下的法线纹理，其坐标系是以像素在以网格法线为z轴，UV方向为X轴和Y轴所组成的某种局部坐标系，知乎大佬说可以理解为是对像素网格法线的扰动。因此，由图像可以看到，其颜色普遍偏蓝，就是因为其z轴靠近1。

那么就可以根据切线坐标系将法线转换到世界坐标系。

数学原理

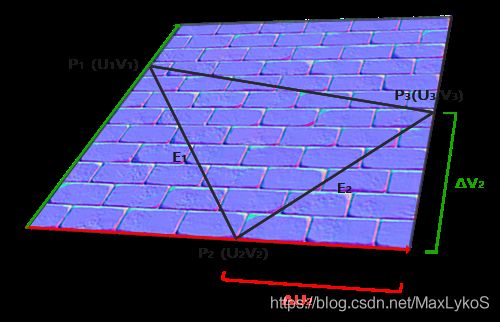
P1P2P3代表网格中的一个三角形，T和B分别代表tangent和bitangent轴，与UV轴对其，UV坐标和三个顶点的模型坐标皆已知。
$$\begin{gathered} P_1-P_2=E_1=\Delta U_{1}T+\Delta V_{1}B \\ {P}_3-P_2=E_2=\Delta U_{2}T+\Delta V_{2}B \end{gathered}$$
可变为
$$\begin{gathered} (E_{1x},E_{1y},E_{1z})=\Delta U_1(T_x,T_y,T_z)+\Delta V_1(B_x,B_y,B_z) \\ (E_{2x},E_{2y},E_{2z})=\Delta U_2(T_x,T_y,T_z)+\Delta V_2(B_x,B_y,B_z) \end{gathered}$$
表示为矩阵
$$\left[\begin{array}{ccc}{E}_{1x}& E_{1y}& E_{1z}\\ E_{2x}& E_{2y}& E_{2z}\end{array}\right]=\left[\begin{array}{cc}\Delta U_1& \Delta V_1\\ \Delta U_2& \Delta V_2\end{array}\right]\left[\begin{array}{ccc}{T}_x& T_y& T_z\\ B_x& B_y& B_z\end{array}\right]$$
左乘逆矩阵，得
$${\left[\begin{array}{cc}\Delta U_1& \Delta V_1\\ \Delta U_2& \Delta V_2\end{array}\right]}^{-1}\left[\begin{array}{ccc}{E}_{1x}& E_{1y}& E_{1z}\\ E_{2x}& E_{2y}& E_{2z}\end{array}\right]=\left[\begin{array}{ccc}{T}_x& T_y& T_z\\ B_x& B_y& B_z\end{array}\right]$$
由
可以推出
$$\left[\begin{array}{ccc}{T}_x& T_y& T_z\\ B_x& B_y& B_z\end{array}\right]=\frac{1}{\Delta U_1\Delta V_2-\Delta U_2\Delta V_1}\left[\begin{array}{cc}\Delta V_2& -\Delta V_1\\ -\Delta U_2& \Delta U_1\end{array}\right]\left[\begin{array}{ccc}{E}_{1x}& E_{1y}& E_{1z}\\ E_{2x}& E_{2y}& E_{2z}\end{array}\right]$$
求出T三个分量即可

float f = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV2.x * deltaUV1.y);

tangent.x = f * (deltaUV2.y * edge1.x - deltaUV1.y * edge2.x);
tangent.y = f * (deltaUV2.y * edge1.y - deltaUV1.y * edge2.y);
tangent.z = f * (deltaUV2.y * edge1.z - deltaUV1.y * edge2.z);
tangent = normalize(tangent);

bitangent.x = f * (-deltaUV2.x * edge1.x + deltaUV1.x * edge2.x);
bitangent.y = f * (-deltaUV2.x * edge1.y + deltaUV1.x * edge2.y);
bitangent.z = f * (-deltaUV2.x * edge1.z + deltaUV1.x * edge2.z);
bitangent = normalize(bitangent);  

左手坐标系还是右手坐标系的区别一般不用考虑。
B可以在着色器中通过法线与施密特正交化后的+T叉乘得到。
float3 B = cross(N, T);

计算出来的T将会保存作为每个顶点的属性，一个三角形上三个顶点共享一个T，但是考虑到三角形与三角形之间会共用顶点，所以可以在每个顶点的TB做平均(assimp应该可以吧)。

计算完之后，在像素着色器里通过法线纹理采样 * TBN矩阵完成法线从切线空间到世界空间的转换。

下面的代码里用了个技巧，计算都是在视图空间进行的，顶点着色器进行MV变换，可以将摄像机放到0,0点，任何坐标都是从摄像机出发指向该坐标的向量。

// PS
cbuffer LightCBuf
{
    float3 lightPos;
    float3 ambient;
    float3 diffuseColor;
    float diffuseIntensity;
    float attConst;
    float attLin;
    float attQuad;
};

cbuffer ObjectCBuf
{
    float specularIntensity;
    float specularPower;
    bool normalMapEnabled;
    float padding[1];
};

Texture2D tex;
Texture2D nmap : register(t2);

SamplerState splr;


float4 main(float3 viewPos : Position, float3 n : Normal, float3 tan : Tangent, float3 bitan : Bitangent, float2 tc : Texcoord) : SV_Target
{
    // sample normal from map if normal mapping enabled
    if (normalMapEnabled)
    {
    	// Orthogonalization
        float3 T = normalize(tan - dot(tan , n) * n); 
        // build the tranform (rotation) into tangent space
        const float3x3 tanToView = float3x3(
            normalize(T),
            normalize(bitan),
            normalize(n)
        );
        // unpack the normal from map into tangent space        
        const float3 normalSample = nmap.Sample(splr, tc).xyz;
        n = normalSample * 2.0f - 1.0f;
        // bring normal from tanspace into view space
        n = mul(n, tanToView);
    }
	// fragment to light vector data
    const float3 vToL = lightPos - viewPos;
    const float distToL = length(vToL);
    const float3 dirToL = vToL / distToL;
	// attenuation
    const float att = 1.0f / (attConst + attLin * distToL + attQuad * (distToL * distToL));
	// diffuse intensity
    const float3 diffuse = diffuseColor * diffuseIntensity * att * max(0.0f, dot(dirToL, n));
	// calculate specular intensity based on angle between viewing vector and reflection vector, narrow with power function
    const float3 specular = att * (diffuseColor * diffuseIntensity) * specularIntensity * pow(max(0.0f, dot(normalize(reflect(vToL, n)), normalize(viewPos))), specularPower);
	// final color
    return float4(saturate((diffuse + ambient) * tex.Sample(splr, tc).rgb + specular), 1.0f);
}

//VS
cbuffer CBuf
{
    matrix modelView;
    matrix modelViewProj;
};

struct VSOut
{
    float3 viewPos : Position;
    float3 normal : Normal;
    float3 tan : Tangent;
    float3 bitan : Bitangent;
    float2 tc : Texcoord;
    float4 pos : SV_Position;
};

VSOut main(float3 pos : Position, float3 n : Normal, float3 tan : Tangent, float3 bitan : Bitangent, float2 tc : Texcoord)
{
    VSOut vso;
    vso.viewPos = (float3) mul(float4(pos, 1.0f), modelView);
    vso.normal = mul(n, (float3x3) modelView);
    vso.tan = mul(tan, (float3x3) modelView);
    vso.bitan = mul(bitan, (float3x3) modelView);
    vso.pos = mul(float4(pos, 1.0f), modelViewProj);
    vso.tc = tc;
    return vso;
}

施密特正交化

t = normalize(t - n * dot(n, t));
原理是将t减去t在n上的分量，则t可与n垂直

模型读取

用assimp

Assimp::Importer imp;
	const auto pScene = imp.ReadFile(fileName.c_str(),
		aiProcess_Triangulate |
		aiProcess_JoinIdenticalVertices |
		aiProcess_ConvertToLeftHanded |
		aiProcess_GenNormals |  
		aiProcess_CalcTangentSpace  // calculate T and B
	);

然后数据就都在pScene的各个mesh里了。
效果