十大机器学习算法之决策树（用于信用风险）

算法原理

Decision Trees (DTs) 是一种用来 classification 和 regression 的无参监督学习方法。其目的是创建一种模型从数据特征中学习简单的决策规则来预测一个目标变量的值。决策树类似于流程图的树结构，分支节点表示对一个特征进行测试，根据测试结果进行分类，树节点代表一个类别。

例如，在下面的图片中，决策树通过if-then-else的决策规则来学习数据从而估测数一个正弦图像。决策树越深入，决策规则就越复杂并且对数据的拟合越好。

决策树的优势:

• 便于理解和解释。树的结构可以可视化出来。训练需要的数据少。其他机器学习模型通常需要数据规范化，比如构建虚拟变量和移除缺失值,不过请注意，这种模型不支持缺失值。

• 由于训练决策树的数据点的数量导致了决策树的使用开销呈指数分布(训练树模型的时间复杂度是参与训练数据点的对数值)。
• 能够处理数值型数据和分类数据。其他的技术通常只能用来专门分析某一种变量类型的数据集。详情请参阅算法。
• 能够处理多路输出的问题。
• 使用白盒模型。如果某种给定的情况在该模型中是可以观察的，那么就可以轻易的通过布尔逻辑来解释这种情况。相比之下，在黑盒模型中的结果就是很难说明清楚。
• 可以通过数值统计测试来验证该模型。这对事解释验证该模型的可靠性成为可能。
• 即使该模型假设的结果与真实模型所提供的数据有些违反，其表现依旧良好。

决策树的缺点:

• 决策树模型容易产生一个过于复杂的模型,这样的模型对数据的泛化性能会很差。这就是所谓的过拟合.一些策略像剪枝、设置叶节点所需的最小样本数或设置数的最大深度是避免出现该问题最为有效地方法。
• 决策树可能是不稳定的，因为数据中的微小变化可能会导致完全不同的树生成。这个问题可以通过决策树的集成来得到缓解。
• 在多方面性能最优和简单化概念的要求下，学习一棵最优决策树通常是一个NP难问题。因此，实际的决策树学习算法是基于启发式算法，例如在每个节点进 行局部最优决策的贪心算法。这样的算法不能保证返回全局最优决策树。这个问题可以通过集成学习来训练多棵决策树来缓解,这多棵决策树一般通过对特征和样本有放回的随机采样来生成。
• 有些概念很难被决策树学习到,因为决策树很难清楚的表述这些概念。例如XOR，奇偶或者复用器的问题。
• 如果某些类在问题中占主导地位会使得创建的决策树有偏差。因此，我们建议在拟合前先对数据集进行平衡。

信息增益

       信息熵：一条信息的信息量和它的不确定性有直接的关系，一个问题不确定性越大，要搞清楚这个问题，需要了解的信息就越多，其信息熵也就越大。

其中P(X)是事件发生的概率。

       特征选择的依据是：遍历所有特征，分别计算，使用这个特征划分数据集前后熵的变化值，然后选择变化值最大（即信息增益最大）的特征作为分裂节点，依次类推。

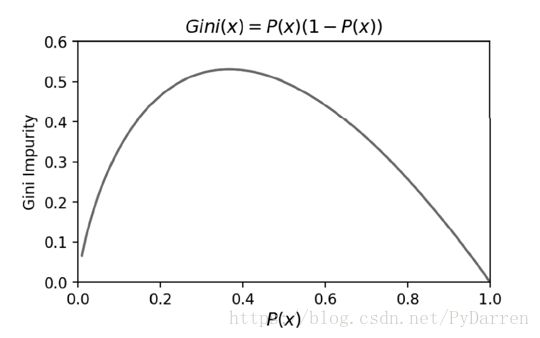
从图可以看出，当概率P(X)接近于0或者1时，信息熵的值越小，其不确定性越小，即数据越纯，其中为1的时候信息熵值为0，是最纯的。在特征选择时，选择信息增益最大的特征，即在物理上让数据朝着更纯净的方向发展。

决策树的创建

       基本步骤（ID3算法）：

• 计算数据集划分前的信息熵；
• 遍历所有未作为划分条件的特征，分别计算根据每个特征划分数据集后的信息熵；
• 选择信息增益最大的特征，利用该特征作为分支节点来划分数据；
• 递归的处理被划分后的子数据集，从未被选择的特征里继续选择最优分类特征来划分子数据集。
• 递归终止的条件：
  1. 没有新的特征来进一步划分数据集；
  2. 信息增益足够小了，需要设定门限值。

几个注意事项

<1> 离散化

如果特征是连续型变量，进行离散化后才可以运用决策树。

<2> 正则项

利用最大化信息增益的原则来选择特征，在决策树构建的过程中，容易选择类别最多的特征来进行分类，比如极端的一种情况——用ID进行分类，毫无意义。

一个解决的办法是，在计算划分子集后的信息熵时，加上一个与类别个数成正比的正则项，来作为最后的信息熵。这样，当算法选择某个分类较多的特征，使信息熵较小时，由于受到类别个数的正则项惩罚，导致最终的信息熵也比较大，这样可以通过参数的选择，达到算法在训练时的某种平衡。

另一种方法是通过信息增益比来作为特征选择的标准。

<3> 基尼不纯度

       信息熵是衡量信息不确定性的指标，实际上也是衡量信息纯度的指标。基尼不纯度是衡量信息不纯度的指标。研究表明，采用这两种算法得到的预测准确率是差不多的，但是采用信息熵时算法的效率会低一些，因为里面有对数运算。

当PX=1时，GiniD=0，即不纯度最低，纯度最高。CART决策树是采用基尼不纯度作为特征选择的一种算法。

1.4 剪枝算法

       在运用决策树的过程中，容易造成过拟合，一种解决办法是进行剪枝处理，分为两种——前剪枝(Pre-Pruning)和后剪枝(Post-Pruning)。

<1> 前剪枝

       前剪枝是在构造决策树时同时进行剪枝。在决策树的创建过程中，如果无法进一步降低信息熵，就停止创建分支。为了避免过拟合，可以设定一个阈值，当信息增益小于这个阈值时，即使可以进一步降低信息熵，也会停止创建分支。还有一些简单的前剪枝方法，如限制叶子节点的样本数，当样本数小于阈值时，停止剪枝。

<2> 后剪枝

       后剪枝是在决策树构造完成之后剪枝。过程是对具有相同父节点的一组点进行检查，判断如果将其合并，信息熵的增加量是否小于某一阈值。如果小于该阈值，则这一组节点合并为一个节点。后剪枝是目前最常用的方法，新节点的类别通过多数原则确定，样本最多的类别作为该节点的类别。

       常用的一种后剪枝算法是降低错误率算法(Reduced-Error Pruning)，其思路是，自底向上，从以构建的决策树中剪去一个子树，并用剪枝后的根节点作为新的叶子节点，从而得到一个简化版的决策树。接着用交叉验证法来测试新旧决策树的准确率，保留准确率高的决策树。遍历所有子树，直到针对交叉验证集无法进一步降低错误率为止。

几种常见算法：

       ID3（Iterative Dichotomiser 3）由 Ross Quinlan 在1986年提出。该算法创建一个多路树，找到每个节点（即以贪心的方式）分类特征，这将产生分类目标的最大信息增益。决策树发展到其最大尺寸，然后通常利用剪枝来提高树对未知数据的泛华能力。

C4.5 是 ID3 的后继者，并且通过动态定义将连续属性值分割成一组离散间隔的离散属性（基于数字变量），消除了特征必须被明确分类的限制。C4.5 将训练的树（即，ID3算法的输出）转换成 if-then 规则的集合。然后评估每个规则的这些准确性，以确定应用它们的顺序。如果规则的准确性没有改变，则需要决策树的树枝来解决。

C5.0 是 Quinlan 根据专有许可证发布的最新版本。它使用更少的内存，并建立比 C4.5 更小的规则集，同时更准确。

CART（Classification and Regression Trees （分类和回归树））与 C4.5 非常相似，但它不同之处在于它支持数值目标变量（回归），并且不计算规则集。CART 使用在每个节点产生最大信息增益的特征和阈值来构造二叉树。scikit-learn 使用 CART 算法的优化版本。

---

# coding: utf-8






# In[2]:

import numpy as np
import pandas as pd
import os,time,datetime


# In[3]:

train_df = pd.read_csv("traindata.csv")
test_df = pd.read_csv("testdata.csv")


# In[4]:

train_df.columns


# In[5]:

X_train = train_df.drop(['Unnamed: 0', 'userId', 'overDued', 'startTime', 'surv'],axis=1).values
y_train = train_df.overDued.values


# In[6]:

X_test = test_df.drop(['Unnamed: 0', 'userId', 'overDued', 'startTime', 'surv'],axis=1).values
y_test = test_df.overDued.values


# In[7]:

from sklearn.tree import DecisionTreeClassifier


# In[8]:

dtc = DecisionTreeClassifier()


# In[9]:

dtc.fit(X_train, y_train)


# In[10]:

dtc.score(X_train, y_train)


# In[11]:

dtc.score(X_test, y_test)


# In[12]:

test_y_predict = dtc.predict(X_test)


# In[13]:

from sklearn.metrics import classification_report


# In[14]:

print(classification_report(y_test, test_y_predict, target_names=['no default', 'default']))


# In[22]:

####优化模型参数
#max_depth决定模型的深度，当到达深度时不再进行分裂
def cv_score(d):
    dtc = DecisionTreeClassifier(max_depth=d)
    dtc.fit(X_train, y_train)
#     train_score = dtc.score(X_train,y_train)
#     cv_score = dtc.score(X_test,y_test)
#     return (train_score,cv_score)
    test_y_predict = dtc.predict(X_test)
    print(classification_report(y_test, test_y_predict, target_names=['no default', 'default'])) 
    print('*' * 100)


# In[23]:

depths = range(2,15)
# score_list = [cv_score(d) for d in depths]
# train_score_list = [s[0] for s in score_list]
# cv_score_list = [s[1] for s in score_list]


# In[24]:

for d in depths:
    cv_score(d)



             precision    recall  f1-score   support

 no default       1.00      0.89      0.94     12137
    default       0.32      0.99      0.48       643

avg / total       0.97      0.89      0.92     12780

****************************************************************************************************
             precision    recall  f1-score   support

 no default       1.00      0.92      0.96     12137
    default       0.40      0.97      0.57       643

avg / total       0.97      0.93      0.94     12780

****************************************************************************************************
             precision    recall  f1-score   support

 no default       1.00      0.91      0.95     12137
    default       0.37      0.98      0.54       643

avg / total       0.97      0.92      0.93     12780

****************************************************************************************************
             precision    recall  f1-score   support

 no default       1.00      0.92      0.96     12137
    default       0.39      0.98      0.56       643

avg / total       0.97      0.92      0.94     12780

****************************************************************************************************
             precision    recall  f1-score   support

 no default       1.00      0.92      0.96     12137
    default       0.40      0.97      0.56       643

avg / total       0.97      0.92      0.94     12780

****************************************************************************************************
             precision    recall  f1-score   support

 no default       1.00      0.92      0.96     12137
    default       0.40      0.97      0.57       643

avg / total       0.97      0.93      0.94     12780

****************************************************************************************************
             precision    recall  f1-score   support

 no default       1.00      0.93      0.96     12137
    default       0.41      0.95      0.58       643

avg / total       0.97      0.93      0.94     12780

****************************************************************************************************
             precision    recall  f1-score   support

 no default       1.00      0.94      0.97     12137
    default       0.44      0.92      0.59       643

avg / total       0.97      0.94      0.95     12780

****************************************************************************************************
             precision    recall  f1-score   support

 no default       0.99      0.94      0.97     12137
    default       0.44      0.91      0.60       643

avg / total       0.97      0.94      0.95     12780

****************************************************************************************************
             precision    recall  f1-score   support

 no default       0.99      0.94      0.97     12137
    default       0.46      0.89      0.60       643

avg / total       0.97      0.94      0.95     12780

****************************************************************************************************
             precision    recall  f1-score   support

 no default       0.99      0.95      0.97     12137
    default       0.47      0.86      0.61       643

avg / total       0.97      0.94      0.95     12780

****************************************************************************************************
             precision    recall  f1-score   support

 no default       0.99      0.95      0.97     12137
    default       0.47      0.83      0.60       643

avg / total       0.96      0.94      0.95     12780

****************************************************************************************************
             precision    recall  f1-score   support

 no default       0.99      0.95      0.97     12137
    default       0.49      0.81      0.61       643

avg / total       0.96      0.95      0.95     12780

****************************************************************************************************