决策树和分类算法
机器学习之决策树
- 非集成学习的算法
- ID3算法
- 信息熵
- 信息增益
- 完整的例子(来自赵卫东的机器学习一书)
- 算法思想(类似贪婪算法)
- 缺陷
- C4.5
- C5.0
- CART
- 集成学习的算法
- 装袋法
- 提升法
- GBDT
- 随机森林
分类算法是利用训练样本集获得分类函数即分类模型(分类器),从而实现将数据集中的样本划分到各个类中。分类模型通过学习训练样本中属性集与类别之间的潜在关系,并以此为依据对新样本属于哪一类进行预测。——分类树算法的含义
一颗决策树由决策结点、分支和叶子结点组成,决策结点表示在样本的一个属性上进行的划分
分支表示对于决策结点进行划分的输出,叶结点代表经过分支到达的分类。
从决策树根结点出发,自顶向下移动,在每个决策结点都会进行次划分,通过划分的结果将样本进行分类,导致不同的分支,最后到达个叶子结点,这个过程就是利用决策树进行分类的过程
例如 一颗外卖订单决策树,椭圆表示决策节点,经历决策节点后都会得到相应的分支,方框即为分类后的叶子节点。

从上述所说,我们大概知道了决策树是什么样子的了,那如何构建一科决策树呢?或者说如何选择相应的属性作为决策绝点会让我们分类后的样本的纯度尽可能高呢?
非集成学习的算法
非集成学习的分类算法属于“弱分类”算法,即分类正确率仅比随机猜测略高的学习算法。
ID3算法
信息熵
为了衡量样本的纯度(就是被分类正确的个数)我们需要先了解一个东东:信息熵??????? (如果你想问为什么这个算法就可以衡量呢?我也不知道,能力有限[认真脸])
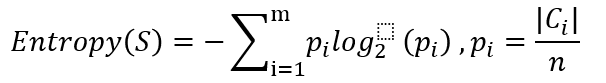
其中,S为分类的样本,Pi为相应分类的概率,譬如:一个大小为10的布尔值样本集S,其中有6个真值、4个假值,那么该布尔型样本分类的熵为:
信息增益
信息熵是衡量分类后样本的纯度,而纯度越高,信息熵的值则会越小(这个可以从公式看出来),熵值减少的部分即为信息增益。其中,E(S)就是信息熵,S为分类后,每个类的个数,Si为分类后每个取值的相应的个数。
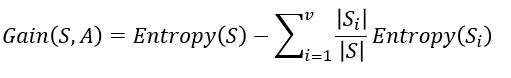
完整的例子(来自赵卫东的机器学习一书)
目标:假设现在以“饮食习性”作为决策节点(你也可以使胎生、水生、会飞),分类属性(结果)为哺乳动物,并计算以饮食习性作为决策点时的信息熵和信息增益。
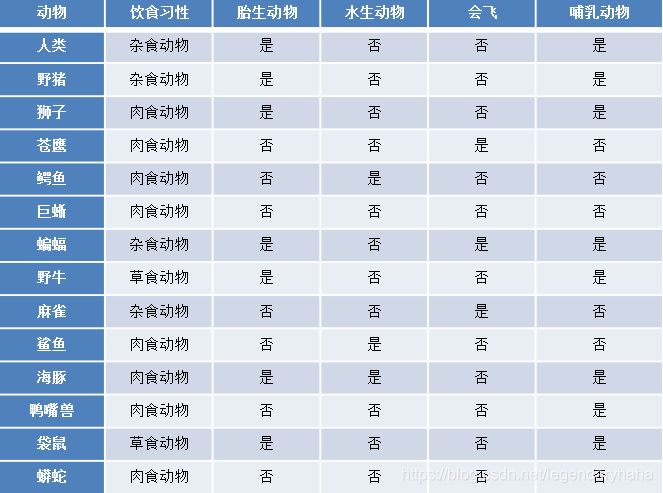
信息熵:样本集总共有14个,在分类目标中,哺乳动物为是的有8个,否为6个,所以得信息熵为:

信息增益:
因为我们是以饮食食性作为决策点的,它有三个取值(杂食、肉食、草食),所以我们根据信息增益的公式,还需要计算分类后的信息熵:
分类后:
- 草食动物:2个是,0个否
- 肉食动物:3个是,5个否
- 杂食动物:3个是,1个否

所以,信息增益为(14个样本,8个肉食,2个草食,4个杂食):
Gain(饮食属性)=0.9852-(8/14*0.9554+2/14*0+4/14*0.8113)=0.2080
算法思想(类似贪婪算法)
- 初始化属性集合和数据集合
- 计算数据集合信息熵S和所有属性的信息熵,选择信息增益最大的属性作为当前决策节点
- 更新数据集合和属性集合(删除掉上一步中使用的属性,并按照属性值来划分不同分支的数据集合)
- 依次对每种取值情况下的子集重复第二步
- 若子集只包含单一属性,则为分支为叶子节点,根据其属性值标记。
- 完成所有属性集合的划分
缺陷
(1)根据信息增益的公式,我们可以发现当分类的类别越多时,分类完后的信息熵的和越小(根据信息熵公式可得),信息增益越大。即ID3算法倾向于选取分裂后有更多属性值的属性作为决策节点。但这是不合理的,我们希望的是分类后的属性尽可能产生更多的信息(譬如:省份,中国人都知道有23个,即使根据省份分类成23个能产生的信息量很少;“中国世界杯能否夺冠”虽然这个属性只有2个“ 能”和“不能”,但它产生的信息确很多;而当一个数据集包含这两个属性时,ID3会选择省份进行分类。)
(2)公式中的计算方式适合离散分布的数据,它的计算类似于求某个点在某个类别出现的概率,即它不具备有连续的特征,在处理离散分布的数据时,效果会差。
C4.5
C4.5算法总体思路与ID3类似,都是通过构造决策树进行分类,其区别在于分支的处理,在分支属性的选取上,ID3算法使用信息增益作为度量,而C4.5算法引入了信息增益率作为度量。

以上面的饮食食性作为例子(14个样本,8个肉食,2个草食,4个杂食):
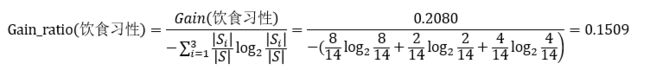
C5.0
C5.0算法是Quinlan在C4.5算法的基础上提出的商用改进版本,目的是对含有大量数据的数据集进行分析,C5.0算法与C4.5算法相比有以下优势:
- 决策树构建时间要比C4.5算法快上数倍
- 生成的决策树规模也更小,拥有更少的叶子结点数
- 使用了提升法(boosting,集成学习的方法),组合多个决策树来做出分类,使准确率大大提高
- 提供可选项由使用者视情况决定,例如是否考虑样本的权重、样本错误分类成本等
CART
CART算法都可以解决回归问题和分类问题,两者的区别如下:
- 都可以对输入进行预测
- 分类问题的输出一般是离散型的(是和否,好人和坏人)
- 回归问题的输出是连续型的(某个连续性函数的值)
CART算法采用的是一种二分循环分割的方法,每次都把当前样本集划分为两个子样本集,使生成的决策树的结点均有两个分支,显然,这样就构造了一个二叉树。
如果分支属性有多于两个取值,在分裂时会对属性值进行组合,选择最佳的两个组合分支。假设某属性存在?个可能取值,那么以该属性作为分支属性,生成两个分支的分裂方法共有2^(?−1)−1种(譬如取值为1,2,3分列方法可以为:12,13,23)
CART算法在分支处理中分支属性的度量指标是Gini(基尼增益指数)指标,假设有K个类,样本点属于第k类的概率为Pk,则概率分布的Gini指数的定义为:

如果样本集合S根据某个特征A被分割为S1,S2两个部分,那么在特征A的条件下,集合S的Gini指数的定义为:
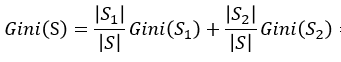
譬如:还是以上面的例子为例:这次以“会飞”作为分裂属性(14个样本,11个不会飞,3个会飞,11个会飞的动物中7个是哺乳动物,4个不是,3个会飞的动物中,1个是哺乳动物,2个不是)
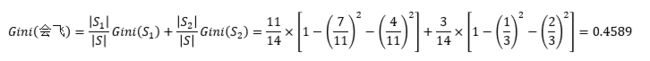
集成学习的算法
将各种弱学习算法进行组合(三个臭皮匠赛过诸葛亮),但是组合之后的效果仍可能高于强学习算法,即集成之后的算法准确率和效率都很高。
装袋法
装袋法(bagging)又称为引导聚集算法(Bootstrap Aggregating),它通过组合多个训练集的分类结构来提升分类效果。
如:假设一个大小为n的训练样本集S,装袋法从样本集S中多次放回采样取出大小为m(m
缺点:装袋法由于多次采样,每个样本被选中的概率相同,因此噪声数据的影响下降,所以装袋法太容易受到过拟合的影响。
提升法
提升法与装袋法类似,对数据集的处理都是一样的,不同的是,提升法在分类过程引入了权重的概念,它给每个单独的训练样本都会分配一个相同的初始权重。
然后进行T轮训练,每一轮中使用一个分类方法训练出一个分类模型,使用此分类模型对所有样本进行分类并更新所有样本的权重:分类正确的样本权重降低,分类错误的样本权重增加,从而达到更改样本分布的目的。
由此可知,每一轮训练后,都会生成一个分类模型,而每次生成的这个分类模型都会更加注意在之前分类错误的样本,从而提高样本分类的准确率。对于新的样本,将T轮训练出的T个分类模型得出的预测结果加权平均,即可得出最终的预测结果。
GBDT
梯度提升决策树(Gradient Boosting Decision Tree)一种迭代的决策树算法,该算法由多棵决策树组成,所有树的结论累加起来做最终答案。它是利用梯度下降的思想,使用损失函数的负梯度在当前模型的值,作为提升树中残差(真实值和预测值之间的差)的近似值,以此来拟合回归决策树。梯度提升决策树的算法过程如下:
- 初始化决策树,估计一个使损失函数最小化的常数构建一个只有根节点的树。
- 不断提升迭代: 计算当前模型中损失函数的负梯度值(负梯度方向下降得最快,而我们的目标就是求一个极小值),作为残差的估计值;估计回归树中叶子节点的区域,拟合残差的近似值; 利用线性搜索估计叶子节点区域的值,使损失函数极小化; 更新决策树。
- 经过若干轮的提升法迭代过程之后,输出最终的模型
随机森林
随机森林是专为决策树分类器设计的集成方式,是装袋法的一种拓展。随机森林与装袋法采取相同的样本抽取方式。
装袋法中的决策树每次从所有属性中选取一个最优的属性作为其分支属性,而随机森林算法每次从所有属性中随机抽取?个属性,然后从这?个属性中选取一个最优的属性作为其分支属性,这样就使得整个模型的随机性更强,从而使模型的泛化能力更强。
而对于参数?的选取,决定了模型的随机性,若样本属性共有M个,?=1意味着随机选择一个属性来作为分支属性,?=属性总数时就变成了装袋法集成方式,通常?的取值为小于log2(M+1)的最大整数。而随机森林算法使用的弱分类决策树通常为CART算法