神经网络解决推荐系统问题（NCF）

前一篇虽然是整理的AFM，但有提到过并行的DeepFM，也自然是还有串行的NFM，本来是想整理这两部分，但是想来它们其实都是利用FM和DNN进行各种各样的组合以提升模型的效果。

所以不管是由共享embedding层的左边FM和右边DNN部分组成，而且可以同时学习到高维和低维的特征的DeepFM；还是串行结合的NFM使用部分非线性点乘以提升多阶交互信息的能力等，他们确实是利用了神经网络DNN结合，在一定程度上解决了普通FM由于计算复杂度往往只用到二阶而且只是线性组合的问题，而AFM也是利用了注意力机制给不同的特征组合加以权重来体现它不同的重要程度。都是基于了FM，而FM某种程度上也是将传统的MF回归化之后的技术，不过其实传统的MF本身是有缺陷的。

MF模型是用户和项目的潜在因素的双向互动，它假设潜在空间的每一维都是相互独立的并且用相同的权重将它们线性结合。因此，MF可视为潜在因素（latent factor）的线性模型。所谓潜在因素就是虽然用户与项目间有交互，但不一定用户就喜欢了，而没交互也不代表不喜欢，这就对隐形学习带来了噪音。

上图展示了的内积函数如何限制MF的表现力。简单来说就是通过计算相似度(如Jaccard相似系数)产生映射时，原本应该与u3更相似的u4将会被排在与u1接近的地方。（如前三个$s_{23}(0.66)>s_{12}(0.5)>s_{13}(0.4)$，而对于u4来说$s_{41}(0.6)>s_{43}(0.4)>s_{42}(0.2)$，便产生了误差）

而NCF直接使用DNN从数据中学习交互函数（以代替MF的内积交互部分），从而突破了由于MF表达时的限制。它的通用框架为：

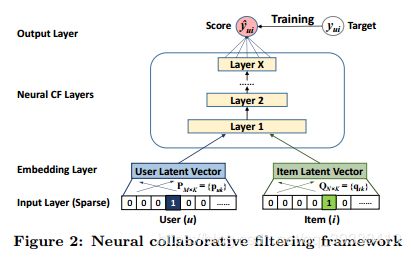
同样是利用Embedding Layer将输入层的稀疏表示映射为一个新的潜在向量。然后分别将用户嵌入和项目嵌入送入多层神经网络结构，它将潜在向量映射为预测分数。$$y_{ui}=f({\mathbf{P}}^T{\mathbf{v}}_u^U,{\mathbf{Q}}^T{\mathbf{v}}_i^I|\mathbf{P},\mathbf{Q},{\Theta }_f),(3)$$
得到损失函数后同样用SGD来训练。通用模型的具体体现在于：

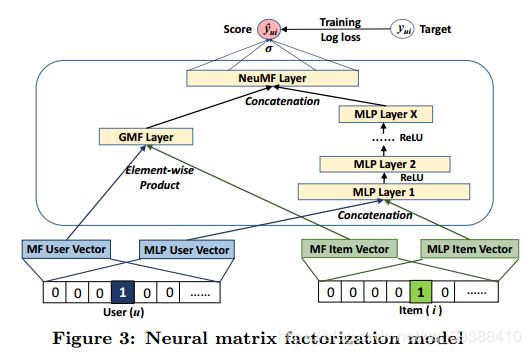
左边是一个GMF。通用矩阵分解，处理线性交互。其中 aout 和 h分别表示输出层的激活函数和连接权重。
$$y_{ui}=a_{out}\left({\mathbf{h}}^T\left({\mathbf{p}}_u\odot {\mathbf{q}}_i\right)\right)$$
右边是MLP模型。多层神经网络，处理非线性交互。其中 Wx, bx 和 ax 分别表示 x 层的感知机中的的权重矩阵，偏置向量（神经网络的神经元阈值）和激活函数。
$${\varphi }_2({\mathbf{z}}_1)=a_2\left({\mathbf{W}}_2^T{\mathbf{z}}_1+{\mathbf{b}}_2\right)$$
$$y_{ui}=\sigma \left({\mathbf{h}}^T{\varphi }_L\left({\mathbf{z}}_{L-1}\right)\right)$$
最后使两者能够做到相互嵌入，使得融合模型具有更大的灵活性。也相当于对于用户-项目矩阵使用了多种方法进行模拟交互来更好的解决潜在问题。
$$\begin{gathered} {\varphi }^{GMF}={\mathbf{p}}_u^G\odot {\mathbf{q}}_i^G, \\ {\varphi }^{MLP}=a_L(W_L^T(a_{L-1}(...a_2(W_2^T\left[\begin{array}{c}{\mathbf{p}}_u^M\\ {\mathbf{q}}_i^M\end{array}\right]+{\mathbf{b}}_2)...))+{\mathbf{b}}_L), \\ {y}_{ui}=\sigma ({\mathbf{h}}^T\left[\begin{array}{c}{\varphi }^{GMF}\\ {\varphi }^{MLP}\end{array}\right]) \end{gathered}$$

需要注意的是：

• GMF和MLP共享嵌入结果。
• 由于是处理embedding后的结果，所以GMF（通用MF）与普通MF不同，公式中使用的是element-wise，即点乘的操作而不是一般的矩阵分解。所以user和item的embedding输出维度需要是一致的。
• MLP默认为3层结构，NeuMF只有一层且使用Sigmoid输出最后的score。

#GMF的代码
def get_model(num_users, num_items, latent_dim, regs=[0,0]):
    #输入变量
    user_input = Input(shape=(1,), dtype='int32', name = 'user_input')
    item_input = Input(shape=(1,), dtype='int32', name = 'item_input')
    #embedding层
    MF_Embedding_User = Embedding(input_dim = num_users, output_dim = latent_dim, name = 'user_embedding',
                                  init = init_normal, W_regularizer = l2(regs[0]), input_length=1)
    MF_Embedding_Item = Embedding(input_dim = num_items, output_dim = latent_dim, name = 'item_embedding',
                                  init = init_normal, W_regularizer = l2(regs[1]), input_length=1)   
    
    # flatten处理，便于后面操作
    user_latent = Flatten()(MF_Embedding_User(user_input))
    item_latent = Flatten()(MF_Embedding_Item(item_input))
    
    #直接合并user_latent, item_latent
    predict_vector = merge([user_latent, item_latent], mode = 'mul')
    
    #得到预测值
    #prediction = Lambda(lambda x: K.sigmoid(K.sum(x)), output_shape=(1,))(predict_vector)
    prediction = Dense(1, activation='sigmoid', init='lecun_uniform', name = 'prediction')(predict_vector)
    
    model = Model(input=[user_input, item_input], 
                output=prediction)

    return model

#MLP部分代码
def get_model(num_users, num_items, layers = [20,10], reg_layers=[0,0]):
    assert len(layers) == len(reg_layers)
    num_layer = len(layers) #MLP层数
    #输入变量
    user_input = Input(shape=(1,), dtype='int32', name = 'user_input')
    item_input = Input(shape=(1,), dtype='int32', name = 'item_input')

    #embedding层，需要强制int一下。维度与GMF是一致的。
    MLP_Embedding_User = Embedding(input_dim = num_users, output_dim = int(layers[0]/2), name = 'user_embedding',
                                  init = init_normal, W_regularizer = l2(reg_layers[0]), input_length=1)
    MLP_Embedding_Item = Embedding(input_dim = num_items, output_dim = int(layers[0]/2), name = 'item_embedding',
                                  init = init_normal, W_regularizer = l2(reg_layers[0]), input_length=1)   
    
    # flatten处理，便于后面操作
    user_latent = Flatten()(MLP_Embedding_User(user_input))
    item_latent = Flatten()(MLP_Embedding_Item(item_input))
    
    #合并embedding层
    vector = merge([user_latent, item_latent], mode = 'concat')
    
    #构建多层MLP
    for idx in xrange(1, num_layer):
        layer = Dense(layers[idx], W_regularizer= l2(reg_layers[idx]), activation='relu', name = 'layer%d' %idx)#Dense层
        vector = layer(vector)
        
    #得到预测值
    prediction = Dense(1, activation='sigmoid', init='lecun_uniform', name = 'prediction')(vector)
    
    model = Model(input=[user_input, item_input], 
                  output=prediction)
    
    return model

评估函数
排名列表的性能由命中率（HR）和归一化折扣累积增益（NDCG）来衡量。由于对所有的item都排序很不现实，所以将随机取100个item进行排序，然后HR会直观地衡量测试项目是否存在于前10名列表中，而NDCG通过将较高分数指定为顶级排名来计算命中的位置。

def getHitRatio(ranklist, gtItem):
    for item in ranklist:
        if item == gtItem:
            return 1
    return 0

def getNDCG(ranklist, gtItem):
    for i in xrange(len(ranklist)):
        item = ranklist[i]
        if item == gtItem:
            return math.log(2) / math.log(i+2)
    return 0

负采样
正如这边文章一开头的那张图中所存在的潜在因素的问题：没交互应该是“？”，并不代表不喜欢“0”，这将带来噪音。所以实际上所用的Movies等数据集并不是真正用于训练的数据集，还需要在此之上模拟一些用户与物品的交互，特别是没有交互记录的“1”其他数据。
而采样操作即是在没有交互记录的“0”中随机抽取一定的数量。如所使用的训练集可以由1个正例+n个负例组成。

def get_train_instances(train, num_negatives):#用于生成真正用于训练的函数
    user_input, item_input, labels = [],[],[]
    num_users = train.shape[0]
    for (u, i) in train.keys():#用户和物品有交互的（u，i），即正例
        # 正例就直接append
        user_input.append(u)
        item_input.append(i)
        labels.append(1)
        # 负例即没有交互的
        for t in xrange(num_negatives):#按照负例采样数目
            j = np.random.randint(num_items) #随机进行选取
            while train.has_key((u, j)):#且不存在交互的物品j
                j = np.random.randint(num_items)
            user_input.append(u)#然后再append
            item_input.append(j)
            labels.append(0)
    return user_input, item_input, labels

所以其实也验证了为什么通用框架建议使用 GMF 和 MLP 的预训练模型来初始化NeuMF，某种程度上也相当于从不同方式模拟和抽象了用户和物品之间的交互，为了更好的学习隐含数据。

其他细节
对于数据集的划分，使用leave-one-out。对每个用户，用最新的交互作为测试集，历史交互为训练集。训练集会使用 get_train_instances函数生成交互模拟用户。而测试集会提前构建好正例-负例对，正例-负例对构建的格式是(userID,itemID)\t negativeItemID1\t negativeItemID2…
针对这些成对数据，用NCF得到评分预测后，通过topk排序的代码为：

import heapq #建堆以高效检索topK
def eval_one_rating(idx):
    #根据用户id，得到相应的item
    rating = _testRatings[idx] #正例
    items = _testNegatives[idx] #负例
    u = rating[0]
    gtItem = rating[1]
    items.append(gtItem)
    
    # Get prediction scores
    map_item_score = {}
    users = np.full(len(items), u, dtype = 'int32')
    #用model预测score
    predictions = _model.predict([users, np.array(items)], 
                                 batch_size=100, verbose=0)
    for i in xrange(len(items)):
        item = items[i]
        map_item_score[item] = predictions[i]
    items.pop()#把正例pop掉再检索
    
    # Evaluate top rank list
    # 堆排速度快，能快速检索
    ranklist = heapq.nlargest(_K, map_item_score, key=map_item_score.get)
    #然后计算两个评估指标
    hr = getHitRatio(ranklist, gtItem)
    ndcg = getNDCG(ranklist, gtItem)
    return (hr, ndcg)

完整代码的逐行源码阅读笔记在：https://github.com/nakaizura/Source-Code-Notebook/tree/master/NCF

关于论文我自己也进行了简单的复现，有什么问题欢迎在评论区一起讨论：

---

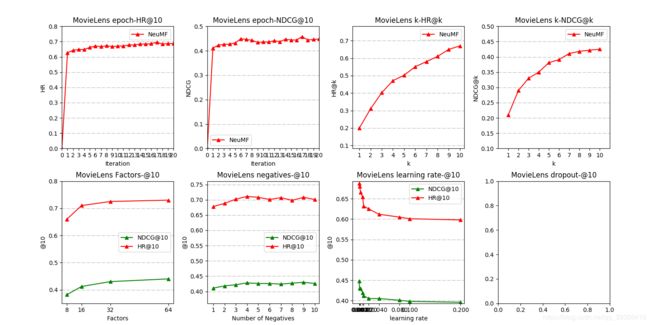
何向南老师在SIGIR 19’和20’又结合Graph的思想，在对user和item的Embedding上做出了新的成果，博主也已经整理了这两篇论文：NGCF，LightGCN 。