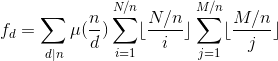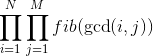gcd求和问题(莫比乌斯反演)
P2522 [HAOI2011]Problem b
P3455 [POI2007]ZAP-Queries
for (int i = 1; i < MAXN; i++) { mu[i] = (mu[i] + mu[i - 1]); phi[i] = (phi[i] + phi[i - 1]); } } int main() { jzk(); int T; sc("%d", &T); while(T--) { ll n, m, d; sc("%lld%lld%lld", &n, &m, &d); ll ans = 0, j; ll minn = min(n, m); for (ll i = 1; i <= minn; i = j + 1) { j = min(n / (n / i), m / (m / i)); ans += (mu[j] - mu[i - 1]) * (n / i / d) * (m / i / d); } pr("%lld\n", ans); } }
P1447 [NOI2010]能量采集
for (int i = 1; i < MAXN; i++) { mu[i] = (mu[i] + mu[i - 1]); phi[i] = (phi[i] + phi[i - 1]); } } int main() { jzk(); ll n, m, d; sc("%lld%lld", &n, &m); ll ans = 0, j; ll minn = min(n, m); for (ll i = 1; i <= minn; i = j + 1) { j = min(n / (n / i), m / (m / i)); ans += (phi[j] - phi[i - 1]) * (n / i) * (m / i); } pr("%lld\n", ans * 2 - n * m); }
P2257 YY的GCD
P2568 GCD
7、令 ![]() , 我们考虑枚举质数
, 我们考虑枚举质数 ![]() 的取值,然后对与每一个满足
的取值,然后对与每一个满足 ![]() 的
的 ![]() ,
,![]() ,即可在
,即可在 ![]() 的时间预处理出
的时间预处理出 ![]() ,得到式子
,得到式子  ,然后使用整除优化,询问时间复杂度
,然后使用整除优化,询问时间复杂度 ![]()
for (int i = 0; i < tot; i++) for (int j = prime[i], cnt = 1; j <= 1e7; j += prime[i], cnt++) g[j] += mu[cnt]; for (int i = 2; i < MAXN; i++) g[i] += g[i - 1]; } int main() { jzk(); int T; sc("%d", &T); while (T--) { ll n, m; sc("%lld%lld", &n, &m); ll minn = min(n, m); ll ans = 0; int j = 0; for (int i = 1; i <= minn; i = j + 1) { j = min(n / (n / i), m / (m / i)); ans += (n / i) * (m / i) * (g[j] - g[i - 1]); } pr("%lld\n", ans); } }
P1829 [国家集训队]Crash的数字表格
P3768 简单的数学题 (需要用到杜教筛)
以第一个式子为例:
2、那么有 ![]() , 通过枚举
, 通过枚举 ![]() 可以将式子
可以将式子 ![F_d=\sum_{i=1}^N\sum_{j=1}^M \frac{i*j}{d}[d|\gcd(i,j)]](http://img.e-com-net.com/image/info8/299b77b233db4e32bec1568b8ef5247e.gif) 化简到
化简到  , 考虑将
, 考虑将 ![]() 同时缩小
同时缩小 ![]() 倍,那么可以将式子化简到
倍,那么可以将式子化简到 
(由于我在第一步中定义函数 ![]() 中重复使用了变量名
中重复使用了变量名 ![]() ,所以上面这个式子的
,所以上面这个式子的 ![]() 的意义是不一样的,
的意义是不一样的,![]() 中的
中的 ![]() 表示的是最大公因数,
表示的是最大公因数,![]() 中的
中的 ![]() 表示的是函数的自变量)
表示的是函数的自变量)
6、所以使用两次整除分块就可以算出上述式子,询问时间复杂度 ![]()
for (int i = 1; i <= MAXN; i++) { mu[i] = mu[i] * i % mod * i % mod + mu[i - 1]; phi[i] += phi[i - 1]; } } ll calc(ll n) { return (n * (n + 1) / 2) % mod; } ll func(ll n, ll m) { ll ans = 0, j; ll minn = min(m, n); for (int i = 1; i <= minn; i = j + 1) { j = min(n / (n / i), m / (m / i)); ans = (ans + (mu[j] - mu[i - 1] + mod) * calc(n / i) % mod * calc(m / i) % mod) % mod; } return ans; } int main() { jzk(); ll n, m; sc("%lld%lld", &n, &m); ll ans = 0, j; ll minn = min(n, m); for (int i = 1; i <= minn; i = j + 1) { j = min(n / (n / i), m / (m / i)); ans = (ans + 1LL * (calc(j) - calc(i - 1) + mod) * func(n / i, m / i)) % mod; } pr("%lld\n", ans); }
P3327 [SDOI2015]约数个数和
7、令  , 所以得到
, 所以得到 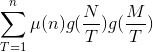 ,一种朴素的方法是,对于每一个
,一种朴素的方法是,对于每一个 ![]() ,使用整除分块来处理,预处理复杂度
,使用整除分块来处理,预处理复杂度 ![]() ,不过也存在线性的解法,对于每一个
,不过也存在线性的解法,对于每一个 ![]() ,求出
,求出 ![]() 的倍数的个数,所以
的倍数的个数,所以 ![]() 实际上就是
实际上就是 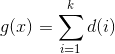 , 其中
, 其中 ![]() 表示约数个数,由于函数
表示约数个数,由于函数 ![]() 是积性函数,可以线性筛出,预处理复杂度
是积性函数,可以线性筛出,预处理复杂度 ![]()
for (int i = 1; i < MAXN; i++) { mu[i] = (mu[i] + mu[i - 1]); phi[i] = (phi[i] + phi[i - 1]); } for (int i = 1; i < MAXN; i++) { ll ans = 0, j; for (int k = 1; k <= i; k = j + 1) { j = i / (i / k); ans += (j - k + 1) * (i / k); } sub[i] = ans; } } int main() { jzk(); int T; sc("%d", &T); while (T--) { ll n, m, d; sc("%lld%lld", &n, &m); ll ans = 0, j; ll minn = min(n, m); for (ll i = 1; i <= minn; i = j + 1) { j = min(n / (n / i), m / (m / i)); ans += (mu[j] - mu[i - 1]) * sub[n / i] * sub[m / i]; } pr("%lld\n", ans);//gcd } }
P3704 [SDOI2017]数字表格
1、先将式子化简,考虑枚举 ![]() ,化简得到
,化简得到 ![\prod_{i=d}^n fib(d)^{\sum_{i=1}^N\sum_{j=1}^M[\gcd(i,j)==d]}](http://img.e-com-net.com/image/info8/4e9c71c5bcb945758b28677339b3b06e.gif) ,显然指数的式子可以化简成
,显然指数的式子可以化简成 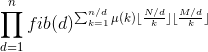
3、令 ![]() ,考虑直接枚举
,考虑直接枚举 ![]() 得到
得到 ![]() ,考虑将括号里面作为一个整体,因为我们知道,函数
,考虑将括号里面作为一个整体,因为我们知道,函数 ![]() 只有三个取值
只有三个取值 ![]() ,所以这个次方只需要预处理
,所以这个次方只需要预处理 ![]() 和 他的逆元即可,然后暴力枚举括号里面的式子,再整除分块即可。
和 他的逆元即可,然后暴力枚举括号里面的式子,再整除分块即可。
4、有一个小优化,由于 ![]() 是质数,所以
是质数,所以 ![]() ,所以可以在整除分块的时候让指数对
,所以可以在整除分块的时候让指数对 ![]() 取模(时间差了一倍),询问时间复杂度
取模(时间差了一倍),询问时间复杂度 ![]()
fib[0] = 0, fib[1] = 1; inv[0] = 0, inv[1] = 1; for (int i = 2; i < MAXN; i++) { fib[i] = (fib[i - 1] + fib[i - 2]) % mod; inv[i] = power(fib[i], mod - 2) % mod; } for (int i = 0; i < MAXN; i++) sub[i] = 1; for (ll d = 1; d < MAXN; d++) { if (mu[d] == 0) continue; for (ll T = d, k = 1; T < MAXN; T += d, k++) { if (mu[d] == 1) sub[T] = (sub[T] * fib[k]) % mod; else if (mu[d] == -1) sub[T] = (sub[T] * inv[k]) % mod; } } inv[0] = power(sub[0], mod - 2); for (int i = 1; i < MAXN; i++) { sub[i] = (sub[i] * sub[i - 1]) % mod; inv[i] = power(sub[i], mod - 2); } } int main() { jzk(); int T; sc("%d", &T); while (T--) { ll n, m; sc("%lld%lld", &n, &m); ll ans = 1, j; ll minn = min(n, m); for (int i = 1; i <= minn; i = j + 1) { j = min(n / (n / i), m / (m / i)); ans = (ans * power(sub[j] * inv[i - 1] % mod, (n / i) * (m / i) % (mod - 1))) % mod; } pr("%lld\n", ans); } }
参考博客链接:
https://blog.csdn.net/fo0old/article/details/82020110
https://blog.csdn.net/jk_chen_acmer/article/details/82708274
莫比乌斯反演公式证明:https://blog.csdn.net/litble/article/details/72804050
分块优化证明:https://blog.csdn.net/outer_form/article/details/50590197
贼详细的各种反演和解释:https://www.luogu.org/blog/An-Amazing-Blog/mu-bi-wu-si-fan-yan-ji-ge-ji-miao-di-dong-xi
![\sum_{i=1}^N \sum_{j=1}^M [gcd(i,j)==k]](http://img.e-com-net.com/image/info8/6fcf305094734463b32ca061f9d3496f.gif)
![f_d=\sum_{i=1}^N \sum_{j=1}^M [\gcd(i,j)==d],\ F_d=\sum_{i=1}^N\sum_{j=1}^M[d|\gcd(i,j)]](http://img.e-com-net.com/image/info8/7792f6a2928e4770976854be2daf3aca.gif)
![F_d=\sum_{i=1}^N\sum_{j=1}^M[d|\gcd(i,j)]](http://img.e-com-net.com/image/info8/293cd9b3a3cf4b948f4f9c83d78e3efd.gif)
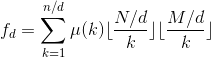

![f_d=\sum_{i=1}^N \sum_{j=1}^M d[\gcd(i,j)==d],\ F_d=\sum_{i=1}^N\sum_{j=1}^M d[d|\gcd(i,j)]](http://img.e-com-net.com/image/info8/891ec5b0c8bc4c6f959430d6898acb74.gif)
![F_d=\sum_{i=1}^N\sum_{j=1}^M d[d|\gcd(i,j)]](http://img.e-com-net.com/image/info8/8d7c74ea8e5445d18f0260bab1edb0fc.gif)
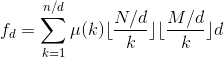
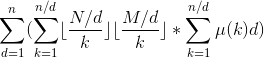
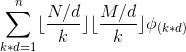
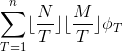
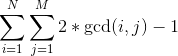
![\sum_{i=1}^N \sum_{j=1}^M [gcd(i,j)\in prime]](http://img.e-com-net.com/image/info8/6828f168357c4c9da60adda03c377ef1.gif)
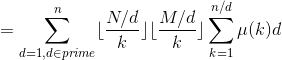


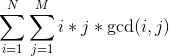
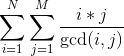

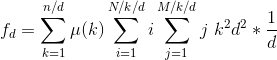

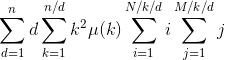
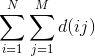
![\sum_{i=1}^N\sum_{j=1}^M\sum_{x|i}\sum_{y|j}[\gcd(x,y)==d]](http://img.e-com-net.com/image/info8/0441a7c078b44ad6a37aa525ecde8ef6.gif)
![\sum_{i=1}^N\sum_{j=1}^M\sum_{i|x}\sum_{j|y} [\gcd(i,j)==d]](http://img.e-com-net.com/image/info8/f2cca8a5b9b04a108de21539ba908f9b.gif)
![\sum_{i=1}^N\sum_{j=1}^M\lfloor\frac{N}{i}\rfloor \lfloor\frac{M}{j}\rfloor [\gcd(i,j)==d]](http://img.e-com-net.com/image/info8/4beb83b9aed642f2ba9cc4d2fac707f3.gif)
![f_d=\sum_{i=1}^N \sum_{j=1}^M \lfloor\frac{N}{i}\rfloor \lfloor\frac{M}{j}\rfloor [\gcd(i,j)==d],\ F_d=\sum_{i=1}^N\sum_{j=1}^M \lfloor\frac{N}{i}\rfloor \lfloor\frac{M}{j}\rfloor [d|\gcd(i,j)]](http://img.e-com-net.com/image/info8/bd45433201d0447ab2db85be0dcd2f5e.gif)
![F_d=\sum_{i=1}^N \lfloor\frac{N}{i}\rfloor \sum_{j=1}^M \lfloor\frac{M}{j}\rfloor [d|\gcd(i,j)]](http://img.e-com-net.com/image/info8/78034e2777d54fb2a2f273c4699e3142.gif)