音频淡入淡出效果——解决音频突变的爆音问题

使用软件调节音量时如果音量之间的步进太大，声音突变，就能听到明显的爆音，尤其以单音音频更为明显，类似的问题还在声音起播、暂停、结束、快进快退时经常会出现，这个时候一般需要对音频进行渐入渐出的效果处理。

先来看一个典型的爆音音频示例，播放一个1k hz的正玄波，并调节音量，可以看到波形幅度增大

由于幅度跳变太大，过渡不连续，造成爆音，从频谱图来看这条竖直的亮线处，就是产生爆音的位置

为解决这个问题，就需要引入渐入渐出处理了，声音由大变小时需要做渐出处理，由小变大时需要做渐入处理

所谓渐入渐出处理就是需要一个平滑的过渡，比如从0到1，可以在中间插几个点，平缓的过渡到1，插多少点和每个点的值带来的效果也不一样。这种处理也应用在各种动画过渡场景中，原理相通。

动画效果中经常用到的缓动公式,有兴趣的同学可以深入研究一下其中的数学原理，有几个相关的资料网页：

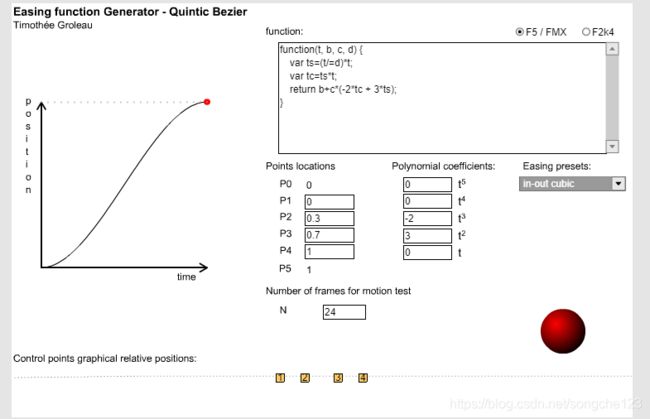
http://www.timotheegroleau.com/Flash/experiments/easing_function_generator.htm

这个网页十分强大，可以手动设计缓动效果并生成对应的函数接口

http://blog.moagrius.com/actionscript/jsas-understanding-easing/

这个网页详细解释了函数公式的意义：

These functions are usually written with 4 arguments [2]:


function noEasing (t, b, c, d) {
	return c * t / d + b;
}
@t is the current time (or position) of the tween. This can be seconds or frames, steps, seconds, ms, whatever – as long as the unit is the same as is used for the total time [3].
@b is the beginning value of the property.
@c is the change between the beginning and destination value of the property.
@d is the total time of the tween.

这里的解释是针对动画效果而言，翻译成音频来说，我们的音量假设从0增大到1.0

b就代表起始音量0，c表示目标音量到起始音量的差即1.0

d意味着需要对多少样本做处理，一般我们会以时间来计算，比如我要200ms内的音频数据缓动处理，那么这么样本总值就是:

d = 200*sr(采样率)/1000  ,因为左右声道是同时处理，我们以frame为单位，48000采样率，d的大小为9600

t就是处理的frame计数了，从0到9600增加，返回值就是当前的frame需要的当前音量，参考代码如下：

vol_delta = target_volume - current_volume;
for (j = 0; j < nframes; j++) {
          if (ease_frames == 0) {
                     current_volume = target_volume;
          } else if (ease_frames_elapsed < ease_frames) {

                        current_volume= floatEaseNext((float)ease_frames_elapsed,
                                                    start_volume, vol_delta, (float)(ease_frames - 1));
                        ease_frames_elapsed++;
                    }
			
                    for (i = 0 ; i < ch; i++) {
                        data[j * ch + i] = data[j * ch + i] * current_volume;
                    }
       }

公式有很多种，每种公式处理的过渡效果不一，这是两种ease in和ease out的处理公式

EaseInCubic:
floatEaseFunc( float t, float b, float c, float d) {
        t /= d;
        return c * t * t * t + b;
}
EaseOutCubic:
       floatEaseFunc( float t, float b, float c, float d) {
         t = t / d - 1;
        return c * (t * t * t + 1) + b;
}

来看一下实际对音频突变的处理效果,这是系统在播放1Khz时不断调整音量时dump的pcm数据

我们从频谱图上来看

整段音频非常干净，没有任何杂音爆破音，处理的相当完美。

据了解缓动公式由大神robert penner提出，再次感谢膜拜大神！