利用ARIMA模型对时间序列进行分析的经典案例（详细代码）

因为之前在学数据分析课程的时候老师讲到时间序列这里，但只是简单的对这个经典的时间序列案例介绍了一下，并没有涉及对差分次数d的查找、找ARIMA模型的p、q值和模型检验 这三个步骤。
后来我搜寻了整个网络，终于结合各个文章的解释，对代码进行了重新的梳理，下面就是详细的整个代码过程（如果问题，欢迎提出来指正！?）：

# -*- coding: utf-8 -*-
# 用 ARIMA 进行时间序列预测
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.tsa.arima_model import ARMA
from statsmodels.graphics.tsaplots import acf,pacf,plot_acf,plot_pacf
from statsmodels.graphics.api import qqplot

# 1.创建数据
data = [5922, 5308, 5546, 5975, 2704, 1767, 4111, 5542, 4726, 5866, 6183, 3199, 1471, 1325, 6618, 6644, 5337, 7064, 2912, 1456, 4705, 4579, 4990, 4331, 4481, 1813, 1258, 4383, 5451, 5169, 5362, 6259, 3743, 2268, 5397, 5821, 6115, 6631, 6474, 4134, 2728, 5753, 7130, 7860, 6991, 7499, 5301, 2808, 6755, 6658, 7644, 6472, 8680, 6366, 5252, 8223, 8181, 10548, 11823, 14640, 9873, 6613, 14415, 13204, 14982, 9690, 10693, 8276, 4519, 7865, 8137, 10022, 7646, 8749, 5246, 4736, 9705, 7501, 9587, 10078, 9732, 6986, 4385, 8451, 9815, 10894, 10287, 9666, 6072, 5418]

data = pd.Series(data)
data.index = pd.Index(sm.tsa.datetools.dates_from_range('1901','1990'))
data.plot(figsize=(12,8))
#绘制时序的数据图
plt.show()

#2.下面我们先对非平稳时间序列进行时间序列的差分，找出适合的差分次数d的值：
#fig = plt.figure(figsize=(12, 8))
#ax1 = fig.add_subplot(111)
#diff1 = data.diff(1)
#diff1.plot(ax=ax1)
#这里是做了1阶差分，可以看出时间序列的均值和方差基本平稳，不过还是可以比较一下二阶差分的效果：

#这里进行二阶差分
#fig = plt.figure(figsize=(12, 8))
#ax2 = fig.add_subplot(111)
#diff2 = data.diff(2)
#diff2.plot(ax=ax2)
#由下图可以看出来一阶跟二阶的差分差别不是很大，所以可以把差分次数d设置为1，上面的一阶和二阶程序我们注释掉

#这里我们使用一阶差分的时间序列
#3.接下来我们要找到ARIMA模型中合适的p和q值：
data = data.diff(1)
data.dropna(inplace=True)
#加上这一步，不然后面画出的acf和pacf图会是一条直线

#第一步：先检查平稳序列的自相关图和偏自相关图
fig = plt.figure(figsize=(12, 8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(data,lags=40,ax=ax1)
#lags 表示滞后的阶数
#第二步：下面分别得到acf 图和pacf 图
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(data, lags=40,ax=ax2)

#由上图可知，我们可以分别用ARMA(0,1)模型、ARMA(7,0)模型、ARMA(7,1)模型等来拟合找出最佳模型：
#第三步:找出最佳模型ARMA
arma_mod1 = sm.tsa.ARMA(data,(7,0)).fit()
print(arma_mod1.aic, arma_mod1.bic, arma_mod1.hqic)
arma_mod2 = sm.tsa.ARMA(data,(0,1)).fit()
print(arma_mod2.aic, arma_mod2.bic, arma_mod2.hqic)
arma_mod3 = sm.tsa.ARMA(data,(7,1)).fit()
print(arma_mod3.aic, arma_mod3.bic, arma_mod3.hqic)
arma_mod4 = sm.tsa.ARMA(data,(8,0)).fit()
print(arma_mod4.aic, arma_mod4.bic, arma_mod4.hqic)

#由上面可以看出ARMA(7,0)模型最佳
#第四步：进行模型检验
#首先对ARMA(7,0)模型所产生的残差做自相关图
resid = arma_mod1.resid
#一定要加上这个变量赋值语句，不然会报错resid is not defined 
fig = plt.figure(figsize=(12, 8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(resid.values.squeeze(),lags=40,ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(resid, lags=40,ax=ax2)

#接着做德宾-沃森（D-W）检验
print(sm.stats.durbin_watson(arma_mod1.resid.values))
#得出来结果是不存在自相关性的

#再观察是否符合正态分布,这里用qq图
fig = plt.figure(figsize=(12,8))
ax = fig.add_subplot(111)
fig = qqplot(resid, line='q',ax=ax, fit=True)

#最后用Ljung-Box检验:检验的结果就是看最后一列前十二行的检验概率（一般观察滞后1~12阶），
#如果检验概率小于给定的显著性水平，比如0.05、0.10等就拒绝原假设，其原假设是相关系数为零。
#就结果来看，如果取显著性水平为0.05，那么相关系数与零没有显著差异，即为白噪声序列。
r,q,p = sm.tsa.acf(resid.values.squeeze(),qstat=True)
data1 = np.c_[range(1,41), r[1:], q, p]
table= pd.DataFrame(data1, columns=[ 'lag','AC','Q','Prob(>Q)'])
print(table.set_index('lag'))

#第五步：模型预测,对未来十年进行预测
predict_y =arma_mod1.predict('1990', '2000', dynamic=True)
#print(predict_y)
fig, ax = plt.subplots(figsize=(12,8))
ax = data.ix['1901':].plot(ax=ax)
predict_y.plot(ax=ax)

最后奉上整个代码运行过程种生成的所有可视化图和结果：
（一开始的时序图）

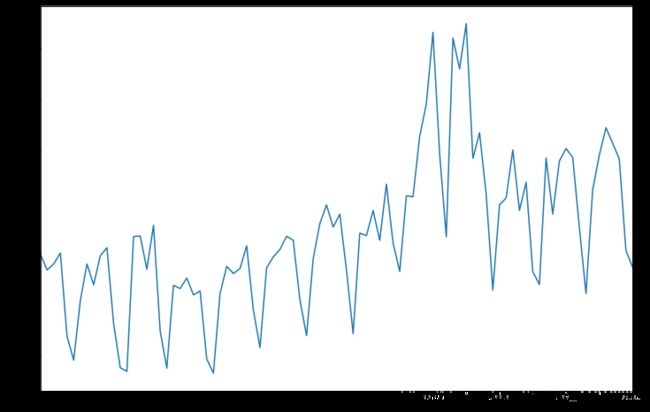
下面是生成的自相关图（acf图）和偏自相关图（pacf图）：

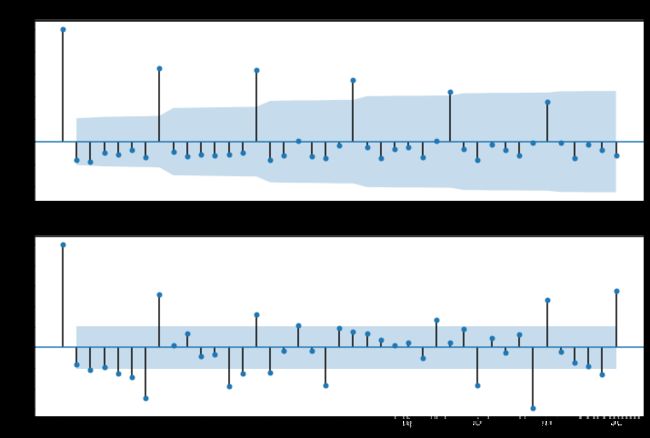
这是找出最佳模型ARMA的数据运行结果：

1580.3025343802506 1602.70026170784 1589.3304155123078
1632.5280687868353  1639.9939778960318 1635.5373624975211
1581.741953757229 1606.6283174545506 1591.7729327928485
1582.0274262666355 1606.913789963957 1592.0584053022549

进行模型检验，首先对ARMA(7,0)模型所产生的残差做自相关和偏自相关图：

这里是德宾-沃森（D-W）检验后的结果：

2.0226619351807082

接着用qq图来观察是否符合正态分布：

然后是用Ljung-Box检验的结果:

            AC          Q  Prob(>Q)
lag                                
1.0  -0.013620   0.017072  0.896043
2.0  -0.048111   0.232545  0.890232
3.0   0.094049   1.065538  0.785399
4.0   0.047719   1.282507  0.864336
5.0   0.157830   3.684276  0.595706
6.0  -0.015497   3.707712  0.716160
7.0  -0.241722   9.478707  0.220088
8.0   0.067333   9.932028  0.269829
9.0  -0.015059   9.954985  0.354142
10.0 -0.250211  16.373227  0.089435
11.0 -0.085557  17.133292  0.103994
12.0 -0.066882  17.603796  0.128261
13.0 -0.099118  18.650747  0.134337
14.0  0.183460  22.285305  0.072939
15.0 -0.224821  27.817186  0.022742
16.0  0.013207  27.836539  0.033070
17.0  0.172933  31.200543  0.018879
18.0 -0.054509  31.539470  0.024912
19.0 -0.059218  31.945201  0.031702
20.0  0.038317  32.117537  0.042062
21.0  0.122530  33.905707  0.037090
22.0  0.105273  35.245351  0.036518
23.0 -0.007281  35.251856  0.049095
24.0 -0.147063  37.946657  0.035111
25.0  0.045061  38.203610  0.044187
26.0 -0.029390  38.314649  0.056605
27.0  0.033956  38.465262  0.070798
28.0  0.125451  40.554803  0.058962
29.0 -0.094511  41.760519  0.059003
30.0 -0.035058  41.929231  0.072578
31.0  0.009097  41.940788  0.090824
32.0 -0.016855  41.981152  0.111447
33.0 -0.045631  42.282283  0.129112
34.0  0.000052  42.282284  0.155724
35.0 -0.023147  42.362642  0.183158
36.0 -0.004809  42.366176  0.215442
37.0 -0.081576  43.402643  0.217174
38.0 -0.086627  44.594344  0.214138
39.0  0.005819  44.599828  0.248019
40.0 -0.066766  45.336624  0.259191
1990-12-31   -1224.754904
1991-12-31    3524.663640
1992-12-31    1267.491272
1993-12-31     661.201862
1994-12-31    -569.545994
1995-12-31    -636.202961
1996-12-31   -2249.722008
1997-12-31    -710.790841
1998-12-31    2719.687594
1999-12-31     970.876673
2000-12-31     279.806969
Freq: A-DEC, dtype: float64

最后生成的预测时序图：

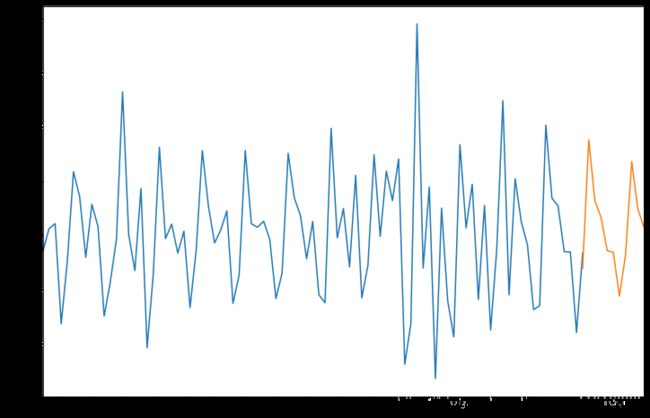
参考资料：
[python] 时间序列分析之ARIMA
Python_Statsmodels包_时间序列分析_ARIMA模型