python数据分析实战之AQI预测
前言:上一篇对AQI进行了分析,这一篇根据对以往的数据,建立一个模型,可以将模型应用于未知的数据,来进行AQI的预测。
文章目录
- 1、加载相关库和数据集
- 2、数据处理和转换
- 2.1 简单的数据处理
- 2.2 数据转换
- 3、建立基模型
- 4、特征选择
- 4.1 RFECV
- 4.2 使用RFECV进行特征选择
- 5、异常值处理
- 5.1 使用临界值进行填充
- 5.2 分箱离散化
- 6 、残差图分析
- 6.1 异方差性
- 6.2 离群点
1、加载相关库和数据集
- 使用的库主要有:pandas、numpy、matplotlib、seaborn、sklearn
- 使用的数据集:2015年空气质量指数(AQI)数据集
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
sns.set(style="darkgrid")
plt.rcParams["font.family"] = "SimHei" # 设置可以显示中文字体
plt.rcParams["axes.unicode_minus"] = False
warnings.filterwarnings("ignore") # 忽略警告信息
data = pd.read_csv("AQI_data.csv") # AQI历史数据集
2、数据处理和转换
2.1 简单的数据处理
# 空值、重复值处理
data.fillna({"Precipitation": data["Precipitation"].median()}, inplace=True)
data.drop_duplicates(inplace=True)
2.2 数据转换
- 对于模型来说,内部进行的都是数学上的运算,所以在进行建模之前,我们需要对类别变量进行数据转换,变成离散变量。
# 将类别变量(是,否)转成离散变量(1,0)
data["Coastal"] = data["Coastal"].map({"是": 1, "否": 0})
data["Coastal"].value_counts()
3、建立基模型
- 不进行任何处理,建立一个基模型,后续的操作都可以在此基础上进行改进。
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
X = data.drop(["City","AQI"], axis=1) # 城市名称对结果不会有影响,所以去除城市列
y = data["AQI"]
# 切分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=0)
lr = LinearRegression()
lr.fit(X_train, y_train) # 使用训练集训练模型
print("训练集R^2:",lr.score(X_train, y_train))
print("测试集R^2:",lr.score(X_test, y_test))
------------------------
训练集R^2: 0.4685357478390665
测试集R^2: 0.3075998035417721
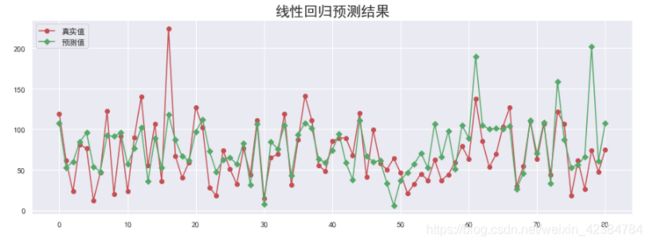
y_hat = lr.predict(X_test)
plt.figure(figsize=(15, 5))
plt.plot(y_test.values, "-r", label="真实值", marker="o")
plt.plot(y_hat, "-g", label="预测值", marker="D")
plt.legend(loc="upper left")
plt.title("线性回归预测结果", fontsize=20)
4、特征选择
- 建立基模型时选择了所有的特征建立模型,但是特征并非越多越好,有些特征可能对模型质量并没有什么改善,我们可以进行删除,同时也可以提高模型训练速度。
- 特征选择的方式有很多,常用的有RFECV方法
4.1 RFECV
- RFECV分成两个部分,分别为RFE和CV。
- RFE(Recursive Feature Elimination):递归特征消除,用来对特征进行重要性评级。
(1)初始的特征集为所有可用的特征
(2)使用当前特征集进行建模,然后计算每个特征的重要性。
(3)删除最不重要的一个(或多个)特征,更新特征集。
(4)跳转到步骤(2),直到完成所有特征的重要性评级。
- CV(Cross Validation):交叉验证,在特征评级后,通过交叉验证,选择最佳数量的特征。
(1)根据RFE阶段确定的特征重要性,依次选择不同数量的特征。
(2)对选定的特征集进行交叉验证
(3)确定平均分最高的特征数量,完成特征选择。
4.2 使用RFECV进行特征选择
from sklearn.feature_selection import RFECV
# estimator: 要操作的模型,step: 每次删除的变量数,cv: 使用的交叉验证折数
# n_jobs: 并发的数量, scoring: 评估的方式。
rfecv = RFECV(estimator=lr, step=1, cv=5, n_jobs=-1, scoring="r2")
rfecv.fit(X_train, y_train)
print(rfecv.n_features_) # 经过选择之后,剩余的特征数量。
-------------------
9
print(rfecv.estimator_) # 经过特征选择后,使用缩减特征训练后的模型。
----------------------
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
print(rfecv.ranking_) # 每个特征的等级,数值越小,特征越重要。
-----------------------
[1 1 1 1 1 1 2 1 1 1]
print(rfecv.support_) # 布尔数组,用来表示特征是否被选择。
------------------------
[ True True True True True True False True True True]
print(rfecv.grid_scores_) # 对应数量特征时,模型交叉验证的评分。
-----------------------------------
[0.05508632 0.21749262 0.2838958 0.28166965 0.28155987 0.26612634
0.26932041 0.31413689 0.31538241 0.30976458]
5、异常值处理
- 如果数据中存在异常值,有可能会对模型效果产生影响,所以建模时非常有必要对异常值进行处理。
- 根据前面分析的介绍,可以使用临界值进行填充和使用分箱法离散化对异常值处理 。
5.1 使用临界值进行填充
- 依据箱线图判断离群点的原则去发现异常值,然后使用临界值对异常值进行填充替换。
- 需要注意的是,应该使用训练集数据去计算临界值,我们在训练期间永远不能使用测试集。
- 箱线图可以用来观察数据整体的分布情况,利用中位数,1/4分位数(Q1),3/4分位数(Q3),上边界,下边界等统计量来描述数据的整体分布情况。
- 箱线图合理范围为 [Q1 - 1.5 IQR, Q3 + 1.5 IQR] (IQR = Q3 − Q1)
# Coastal是类别变量,映射为离散变量,不会有异常值。
for col in X.columns.drop("Coastal"):
if pd.api.types.is_numeric_dtype(X_train[col]):
quartile = np.quantile(X_train[col], [0.25, 0.75])
IQR = quartile[1] - quartile[0] # 计算 IQR
lower = quartile[0] - 1.5 * IQR # 计算下边界
upper = quartile[1] + 1.5 * IQR # 计算上边界
X_train[col][X_train[col] < lower] = lower # 对小于下边界的数用下边界值进行替换
X_train[col][X_train[col] > upper] = upper # 对大于上边界的数用上边界值进行替换
X_test[col][X_test[col] < lower] = lower
X_test[col][X_test[col] > upper] = upper
使用临界值处理之后的训练集再次进行训练,观察是否有改进:
lr.fit(X_train, y_train) # 再次使用训练集训练模型
print("训练集R^2:",lr.score(X_train, y_train))
print("测试集R^2:",lr.score(X_test, y_test))
------------------------------------------- # 相比处理之前有轻微改善,但不是很明显
训练集R^2: 0.48091353214900345
测试集R^2: 0.3284512692284217
再次使用RFECV进行特征选择:
# estimator: 要操作的模型,step: 每次删除的变量数,cv: 使用的交叉验证折数
# n_jobs: 并发的数量, scoring: 评估的方式。
rfecv = RFECV(estimator=lr, step=1, cv=5, n_jobs=-1, scoring="r2")
rfecv.fit(X_train, y_train)
print(rfecv.n_features_) # 经过选择之后,剩余的特征数量。
----------------------------
9
print(rfecv.estimator_) # 经过特征选择后,使用缩减特征训练后的模型。
----------------------------
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
print(rfecv.ranking_) # 每个特征的等级,数值越小,特征越重要。
--------------------------------------
[1 1 1 1 1 1 2 1 1 1]
print(rfecv.support_) # 布尔数组,用来表示特征是否被选择。
---------------------------------------
[ True True True True True True False True True True]
print(rfecv.grid_scores_) # 对应数量特征时,模型交叉验证的评分
-------------------------------------------------------
[0.05508632 0.2109287 0.25972937 0.23394533 0.2541774 0.25827203
0.35205041 0.3593648 0.3769399 0.36918705]
print("剔除的变量:", X_train.columns[~rfecv.support_])
-----------------------------------
剔除的变量: Index(['PopulationDensity'], dtype='object')
经过临界值处理和RFECV进行特征选择之后,效果改进仍然不是很明显,可以使用分箱离散化进行进一步处理。
5.2 分箱离散化
-
分箱离散化是一种数据预处理技术,用于减少次要观察误差的影响,是一种将多个连续值分组为较少数量的“分箱”的方法 (如将人的年龄按照一定的区间进行分组)。
-
分箱后,不能将每个区间都映射为离散数值,而是应当使用One-Hot编码。
-
将离散型特征使用One-Hot编码,是为了让特征之间的距离计算更加合理,详情请戳 机器学习:数据预处理之独热编码(One-Hot)
from sklearn.preprocessing import KBinsDiscretizer
k = KBinsDiscretizer(n_bins=[4, 5, 14, 6], encode="onehot-dense", strategy="uniform")
"""
KBinsDiscretizer K个分箱的离散器,用于将数值变量(通常是连续变量)进行区间离散化操作。
n_bins:分箱(区间)的个数
encode:离散化编码方式,分为:onehot(使用独热编码,返回稀疏矩阵。),
onehot-dense(使用独热编码,返回稠密矩阵),
ordinal(使用序数编码(0,1,2……))。
strategy:分箱的方式,分为:uniform(每个区间的长度范围大致相同。),
quantile(每个区间包含的元素个数大致相同。),
kmeans(使用一维kmeans方式进行分箱)。
"""
discretize = ["Longitude", "Temperature", "Precipitation", "Latitude"] # 定义离散化的特征
X_train_eli = X_train[X_train.columns[rfecv.support_]] # 特征选择剔除后的数据
X_test_eli = X_test[X_test.columns[rfecv.support_]]
r = k.fit_transform(X_train_eli[discretize])
r = pd.DataFrame(r, index=X_train_eli.index)
X_train_dis = X_train_eli.drop(discretize, axis=1) # 获取除离散化特征之外的其他特征。
X_train_dis = pd.concat([X_train_dis, r], axis=1) # 将离散化后的特征与其他特征进行重新组合。
# 对测试集进行同样的离散化操作。
r = pd.DataFrame(k.transform(X_test_eli[discretize]), index=X_test_eli.index)
X_test_dis = X_test_eli.drop(discretize, axis=1)
X_test_dis = pd.concat([X_test_dis, r], axis=1)
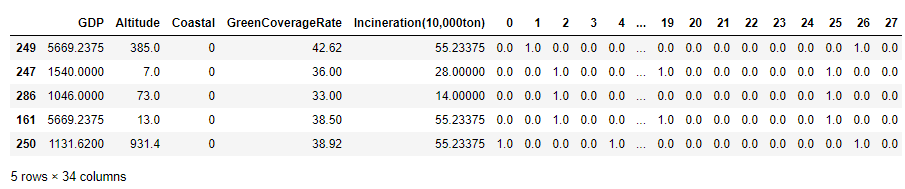
print(X_train_dis.head()) # 查看分箱离散化之后的数据。
使用分箱离散化之后的训练集再次进行训练,观察是否有改进:
lr.fit(X_train_dis, y_train) # 再次使用训练集训练模型
print("训练集R^2:",lr.score(X_train_dis, y_train))
print("测试集R^2:",lr.score(X_test_dis, y_test))
-------------------------------------------------
训练集R^2: 0.673533202788688
测试集R^2: 0.6570961283642467
从上面可以看出,分箱离散化之后,模型效果有了进一步的提升。
6 、残差图分析
- 残差,就是模型预测值与真实值之间的差异。
- 我们可以绘制残差图,来对回归模型进行评估,残差图的横坐标为预测值,纵坐标为残差值。
- 对于一个好的回归模型,误差应该是随机分配的。因此,残差也应随机分布于中心线附近。如果我们从残差图中找出规律,这意味着模型遗漏了某些能够影响残差的解释信息。
lr = LinearRegression()
lr.fit(X_train_dis, y_train) # 使用异常值处理后的数据进行训练
y_hat = lr.predict(X_test_dis)
residual = y_hat - y_test.values # 预测值与真实值之间的差异
plt.xlabel("预测值")
plt.ylabel(" 残差")
plt.axhline(y=0, color="red")
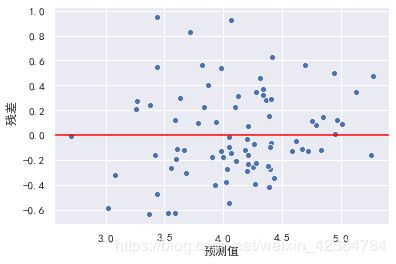
sns.scatterplot(x=y_hat, y=residual)
从上图可以看出,随着预测值的增大,模型的误差也在增大,所以需要进一步处理。
6.1 异方差性
- 异方差性,是指残差具有明显的方差不一致性。
- 对于异方差性,可以使用对目标y值取对数的方式处理。
lr = LinearRegression()
y_train_log = np.log(y_train)
y_test_log = np.log(y_test)
lr.fit(X_train_dis, y_train_log) # 使用对数处理后的数据进行训练
y_hat = lr.predict(X_test_dis)
residual = y_hat - y_test_log.values # 预测值与真实值之间的差异
plt.xlabel("预测值")
plt.ylabel(" 残差")
plt.axhline(y=0, color="red")
sns.scatterplot(x=y_hat, y=residual)
此时,异方差性得到解决,同时,模型的效果也可能会得到一定的提升。
6.2 离群点
- 如果是简单线性回归,可以通过绘制回归线看出是否存在一些离群点。
- 如果多元线性回归,其回归线已经扩展成为超平面,无法通过可视化进行观察,需要通过残差图中的预测值与实际值之间的关系,来检测离群点。
lr = LinearRegression()
# 使用异常值处理后的数据进行训练,此处不结合对数处理使用,只是介绍另外一种优化方式。
lr.fit(X_train_dis, y_train)
y_hat_train = lr.predict(X_train_dis) # 使用训练集本身进行预测,目的是找出训练集的异常值
residual = y_hat_train - y_train.values
r = (residual - residual.mean()) / residual.std()
plt.xlabel("预测值")
plt.ylabel(" 残差")
plt.axhline(y=0, color="red")
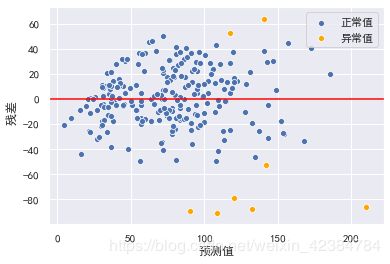
sns.scatterplot(x=y_hat_train[np.abs(r) <= 2], y=residual[np.abs(r) <= 2], color="b", label="正常值")
sns.scatterplot(x=y_hat_train[np.abs(r) > 2], y=residual[np.abs(r) > 2], color="orange", label="异常值") # 大于2倍标准差
去除离群点后,重新进行训练:
X_train_dis_filter = X_train_dis[np.abs(r) <= 2]
y_train_filter = y_train[np.abs(r) <= 2]
lr.fit(X_train_dis_filter, y_train_filter)
print(lr.score(X_train_dis_filter, y_train_filter))
print(lr.score(X_test_dis, y_test))
-----------------------------------------
0.7068375186764522
0.6874497313003948
从以上结果来看,训练效果有了进一步的提升,模型建立完成,后续有未知数据,即可进行AQI的预测。