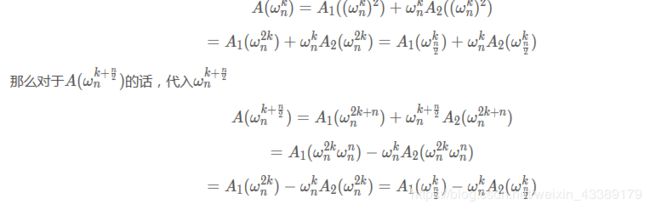快速傅里叶变换学习FFT并通过Python进行实现
前言：最近在一些数据，需要在频域上进行分析，所以就学习了一下FFT，在这里把自己的学习内容梳理一下，有需求的小伙伴可以参考一下。
一、DFT概述
在学习快速傅里叶变换FFT之前，要先了解一下周期性离散时间傅里叶变换DFT.首先我们要搞清楚傅里叶变化的作用什么。DFT(FFT)的作用:可以将信号从时域变换到频域，而且时域和频域都是离散的，通俗的说，可以求出一个信号由哪些正弦波叠加而成，求出的结果就是这些正弦波的幅度和相位。（了解过傅里叶变换的同学都知道，傅里叶变换一般都是在S平面进行的，这是因为信号是一系列正弦波的乘积叠加(为什么是相乘在下面有讲)，而乘法运算在S平面比较好运算，复数相乘为幅值相乘相角相加）。连续信号没法处理的，必须进行离散处理，而离散说白了其实也就是在信号上取任意个点
DFT的公式：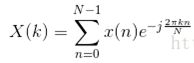
其中x(n)表示DFT变换后的数据，X(k)为采样的模拟信号,公式中的X(k)可以为复信号.之后再带入欧拉公式
就可以得到
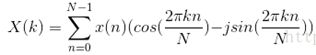
由此可知，傅里叶变换后的第k个点对应的是一个复数。由于余弦信号也一种相位发生π/2移动的正弦信号，因此，这也意味着DFT将时序信号转换成了正弦信号的叠加。由于频率相同的正弦信号的叠加仍然是相同频率的正弦信号，由此可知，变换后的第k点的实部和虚部对应的是一个相同频率的正弦信号，只是相位不同。随着k的变换余弦信号的频率也在发生变换，这也就解释了为什么DFT能够将时序信号转化成不同频率的正弦信号的叠加。
二、FFT概述
FFT其实就是用点值表示法去替代系数表示法，时间复杂度从O(n²)减少到O(nlog2n)
对于两个用系数表示的多项式，我们把它们相乘
设两个多项式分别为A(x),B(x)
我们要枚举A每一位的系数与B每一位的系数相乘，那么系数表示法做多项式乘法时间复杂度O(n²)。但两个用点值表示的多项式相乘，只需要O(n)的时间
n次单位根
n次单位根的概念很重要,对于任意系数多项式转点值，当然可以随便取任意n个x值代入计算,其实可以代入一组神奇的x，代入以后不用做那么多的次方运算,这些x当然不是乱取的，而且取这些xx值应该就是 傅里叶 的主意了.
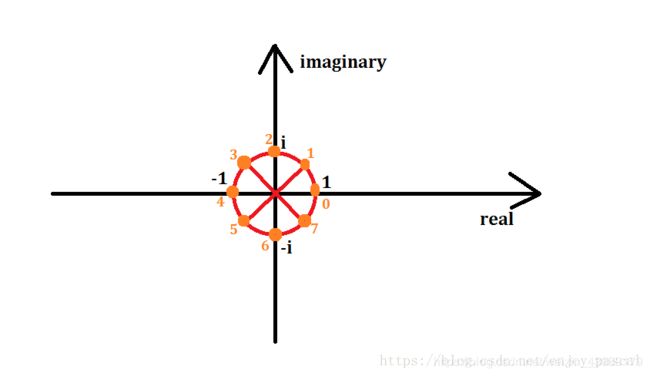橙色点即为n=8时要取的点，从(1,0)点开始，逆时针从0号开始标号，标到7号,记编号为kk的点代表的复数值为ωknωnk，那么由模长相乘，极角相加可知(ωn1)k=ωnk
其中ω1n称为n次单位根，而且每一个ω都可以求出
ωkn=coskn2π+isinkn2πωnk=cosnk2π+isinnk2π
那么ω0n,ω1n,…,ωn−1nωn0,ωn1,…,ωnn−1即为我们要代入的x0,x1,…,xn−1x0,x1,…,xn−1
n次单位根有以下几个性质比较重要：
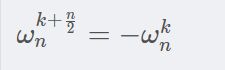
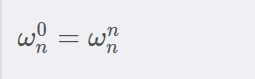
证明就不证了，结合图还是很好理解的。
但DFT可以分治来做，于是 FFT（快速傅里叶变换） 就出来了
首先设一个多项式A(x)
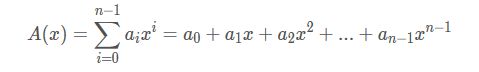
按A(x)下标的奇偶性把A(x)A(x)分成两半，右边再提一个x
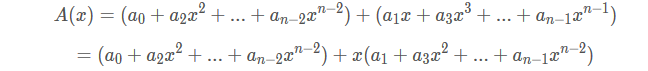
两边好像非常相似，于是再设两个多项式A1(x),A2(x)，令
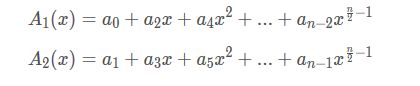
比较明显得出
A(x)=A1(x²)+xA2(x²)
再设k 直接上代码`：
三、Python实现快速傅里叶变换FFT
import numpy as np
from scipy.fftpack import fft,ifft
import matplotlib.pyplot as plt
#采样点选择1400个，因为设置的信号频率分量最高为400赫兹，根据采样定理知采样频率要大于信号频率2倍，所以这里设置采样频率为1000赫兹
x=np.linspace(0,1,1000,endpoint=False)#创建等差数列,endpoint必须是False否则采样异常
#10cos(2pi*f*t - 60/180*pi)表示频率为f相位为-60幅值为10的正弦
y=2 + 4*np.sin(2*np.pi*100*x) + 6*np.sin(2*np.pi*200*x) + 8*np.sin(2*np.pi*300*x)+10*np.sin(2*np.pi*400*x)
yy=fft(y)#快速傅里叶变换
yreal = yy.real# 获取实数部分
yimag = yy.imag# 获取虚数部分
yf=abs(fft(y)) # 取绝对值
yf1=yf/(len(x)/2) #归一化处理 交流是N/2 直流是N
yf1[0] = yf1[0]/2
yf2 = yf1[range(int(len(x)/2))] #由于对称性，只取一半区间
xf = np.arange(len(y)) # 频率 arange支持步长为小数，返回的是队列
xf1 = xf
xf2 = xf[range(int(len(x)/2))] #取一半区间
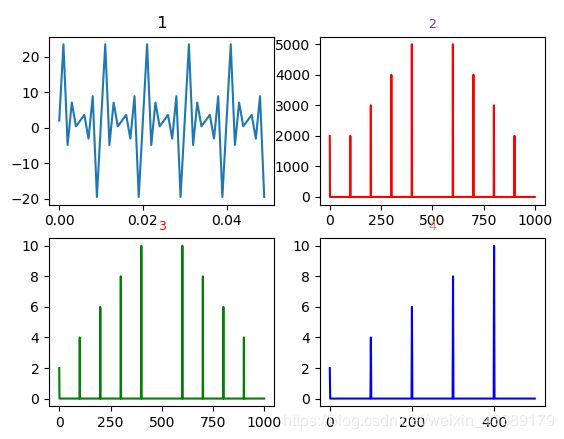
plt.subplot(221)# 第一行的左图
plt.plot(x[0:50],y[0:50])
plt.title('1')
plt.subplot(222)# 第一行的右图
plt.plot(xf,yf,'r')
plt.title('2',fontsize=9,color='#7A378B') #注意这里的颜色可以查询颜色代码表
plt.subplot(223)
plt.plot(xf1,yf1,'g')
plt.title('3',fontsize=9,color='r')
plt.subplot(224)
plt.plot(xf2,yf2,'b')
plt.title('4',fontsize=9,color='#F08080')
plt.show()`
