用A*算法求解八数码问题 java实现

1.估价函数

首先定义估价函数。计算一个节点的估价函数，可以分成两个部分：g(n)已经付出的代价（起始节点到当前节点）和h(n)将要付出的代价（当前节点到目标节点）。节点n的估价函数f(n)定义为f(n)=g(n)+h(n)。在A搜索算法中使用的就是估价函数f(n)=g(n)+h(n)。
接下来定义最优估价函数f*(n)=g*(n)+h*(n),其中g*(n)为起点到n状态的最短路径代价值，h*(n)是n状态到目的状态的最短路径的代价值。这样f*(n)就是起点出发通过n状态而到达目的状态的最佳路径的总代价值。但在绝大部分实际问题中并不存在f*(n)这样的先验函数，但可以将f(n)作为f*(n)的一个近似估计函数。在A及A搜索算法中，g(n)作为g(n)的近似估价。g(n)与g*(n)可能并不相等，但在搜索过程中有g(n)>=g*(n),当搜索过程中已发现了到达n状态的最佳状态时，它们才相等。同样，可以用h(n)代替h*(n)作为n状态到目的状态的最小代价估计值。虽然在绝大数情况下无法计算h*(n)，但是要判别某一h(n)是否大于h*(n)还是可能的。所以如果A搜索算法所使用的估价函数f(x)所能达到的f(n)中的h(n)<=h*(n)时它就为A*搜索算法

2.搜索过程

启发式图搜索算法使用两张表记录状态信息：在open表中保留所有已生产而未扩展的状态。在closed表中记录已扩展过的状态。算法中是根据某些启发信息来排列open表的。它既不同于宽度优先使用的队列，也不同于深度优先所使用的堆栈，而是按一个状态的启发估价函数值的大小排列的一个表。进入open表的状态不是简单地排在队尾或队首，而是根据其估值的大小插入到表中合适的位置，每次从表中优先取出启发估价函数最小的状态加以扩展。
A*算法的搜索过程是基于估价函数的一种加权启发式图搜索算法，搜索过程如下：
1.把初始结点放入到open表
2.若open表为空，则搜索失败，退出
3.移出open表中第一个结点N放入closed表中，也就是估价函数最小的节点，并顺序编号n
4.若目标结点的状态等于结点N的状态，则搜索成功，结束
5.若N不可扩展则转步骤2
6.扩展节点N，生成一组节点N的子节点，对这组子节点做如下操作：
(1)考察是否有已在open表或closed表中存在的结点。若有则再考察其中有无N的先辈结点，若有则删除之，对于其余节点也删除，但由于它们又被第二次生成，因此需要考虑是否修改已经存在于open表或closed表中的这些结点及其后裔的返回指针和f(x)的值。修改原则是：选f(x)值小的路径走。
(2)为其余子节点配上指向N的返回指针后放入open表中，并对open表按f(x)值以升序排序，转向步骤2

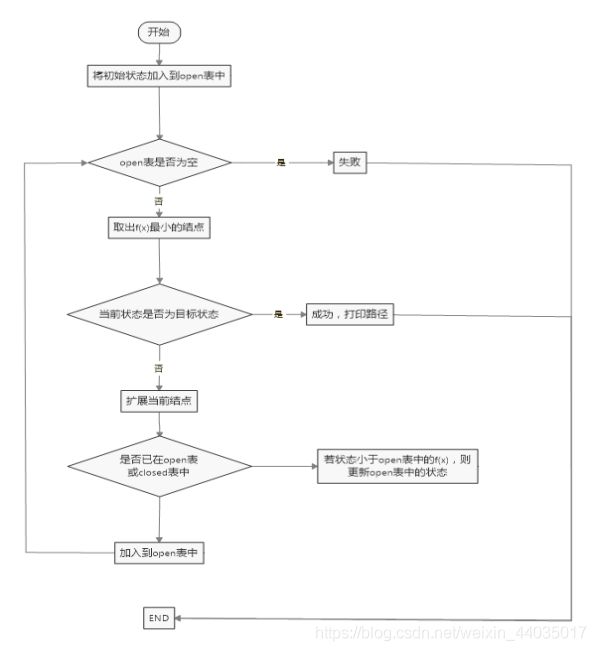
3.流程图

4.八数码的估计函数设计

估计函数是由两部分构成的，节点深度d(n)其实就是当前已经走的步数，不用额外设计函数；启发函数h(n)是比较重要的一个部分，启发函数的设计直接影响了估计函数的效率，有几种定义方法：
(1)当前节点与目标节点差异的度量 => 当前结点与目标节点相比，位置不符的数字个数
(2)当前节点与目标节点距离的度量 => 当前结点与目标节点格局位置不符的数字移动到目标节点中对应位置的最短距离之和
估计函数一：
八数码的g(n)为已经搜索的步数，八数码的h(n)为当前结点与目标节点差异的数量
估计函数二：
当前结点与目标节点格局位置不符的数字移动到目标节点中对应位置的最短距离之和

5.编码实现

package Astatr;

import java.util.*;


public class Astar {
    private int N=3;
    Scanner input=new Scanner(System.in);
    int Map[][]=new int[N][N];
    int target[][]=new int[N][N];
    List<Node> openList=new ArrayList<>();    //A*算法open列表
    List<Node> closeList=new ArrayList<>();   //A*算法closed列表

    List<Node> queue=new ArrayList<>();   //bfs队列

    HashMap<Integer,int []> targetmap=new HashMap<>();  //估价函数二所用的映射功能
    List<Node>  nodeList=new ArrayList<>();  //节点列表用于存储所有扩展节点

    Node Start;
    Node Target;
    Comparator<Node> comparator=new Comparator<Node>() {    //比较函数，根据f(n)的值可以将openlist或closedlist从小到大排列
        @Override
        public int compare(Node o1, Node o2) {
            if(o1.getF()>o2.getF())
                return 1;
            else if(o1.getF()==o2.getF())
                return 0;
            else
                return -1;
        }
    };

    public Astar(){
        if(init()) {
            A_algorithm();    //可以更改为bfs()测试bfs的性能
        }else{
            System.out.println("无解");
        }
    }
    boolean init(){         //初始化函数,用于输入初始八数码和目标八数码
        System.out.println("请输入八数码的初始状态:");
       for(int i=0;i<N;i++){
           for(int j=0;j<N;j++){
               Map[i][j]=input.nextInt();
           }
       }
       Start=new Node();
       Start.setState(Map);
        System.out.println("请输入八数码的目标状态:");
        for(int i=0;i<N;i++){
            for(int j=0;j<N;j++){
                target[i][j]=input.nextInt();
                int index[]={i,j};
                targetmap.put(target[i][j],index);
            }
        }
       Target=new Node();
        Target.setState(target);
        if(isSolve(Target)){
            return true;
        }else{
            return false;
        }
    }
    public boolean isSolve(Node target){     //判断是否有解
        int startNum[]=new int[N*N];
        int endNum[] = new int[N*N];
        int st = 0;
        int et = 0;
        for (int i = N * N - 2; i >= 0; i--) {
            for (int j = i - 1; j >= 0; j--) {
                if (startNum[i] > startNum[j])
                    st++;
                if (endNum[i] > endNum[j])
                    et++;
            }
        }
        if (st % 2 == et % 2)
            return true;
        return false;
    }

    int IndexInList(List<Node> list,Node node){    //判断某一状态是否在列表中 
        for (int index = 0; index < list.size(); index++) {
            int i = 0,j=0;
            for (i = 0; i <N; i++) {
                for(j=0;j<N;j++) {
                    if ((list.get(index).getState()[i][j]) != node.getState()[i][j])
                        break;
                }
                if (j < N)
                    break;
            }
            if (i==N&&j==N) {
                return index;
            }
        }
        return -1;
    }

    public boolean isCanMove(int x,int y){    //是否可以移动0
        if(x<0||x>=3||y<0||y>=3){
            return false;
        }
        return true;
    }
    Node getNext(Node now,int direction){   //移动函数，用于获得下一状态
        int dx[]=new int[]{0,0,-1,1};
        int dy[]=new int[]{-1,1,0,0};
        Node next=new Node();
        int temp[][]=new int[N][N];
        for(int i=0;i<N;i++){
            for(int j=0;j<N;j++)
                temp[i][j]=now.getState()[i][j];
        }
        int zeroIndex[]=now.getZeroIndex();
        int x0=zeroIndex[0];
        int y0=zeroIndex[1];
        int nextZeroIndex=0;
        int nextx,nexty;
        nextx=x0+dx[direction];
        nexty=y0+dy[direction];
        if(isCanMove(nextx,nexty)){
            temp[x0][y0]=now.getState()[nextx][nexty];
            temp[nextx][nexty]=0;        
           List<Node> path=new ArrayList<>();
            path.addAll(now.path);
            next.setState(temp);
            next.setPath(path);
            return next;
        }else{
            return null;
        }
    }

    void A_algorithm(){       //A*算法主体
    Start.setUp2();    //设置估价函数，可以更改为其他估价函数
    Start.path.add(Start);
    openList.add(Start);
    nodeList.add(Start);
    while(!openList.isEmpty()){
        openList.sort(comparator);
        Node best=openList.get(0);
        openList.remove(0);
        closeList.add(best);
        if(best.isTarget(Target)){        //判断是否为目标状态
            System.out.println("-------打印路径------");
            for(int i=0;i<best.path.size();i++){
                System.out.println("第"+i+"次移动");
                best.path.get(i).print();
            }
            System.out.println("共扩展了"+nodeList.size()+"个节点");
            return;
        }
        for(int i=0;i<4;i++){
            Node next=getNext(best,i);
            if(next!=null){       //是否可以移动到下一个状态
                if(IndexInList(closeList,next)==-1){     //如果不在cloesd列表中
                    int index=IndexInList(openList,next);
                    if(index>=0){       //如果在open列表中
                        if(next.getG()<openList.get(index).getG()){    //比较和已在open列表中的深度比较
                            openList.remove(index);     //如果next更小，则将open中已存在的更换为next
                            next.setParent(best);
                            next.setUp2(Target,targetmap);   //设置估价函数，可以更改为其他估价函数
                            next.path.add(next);
                            openList.add(next);
                            nodeList.add(next);
                        }
                    }else{    //如果不在open列表中，则加入到open列表中
                        next.setParent(best);
                        next.setUp2(Target,targetmap);   //设置估价函数，可以更改为其他估价函数
                        next.path.add(next);
                        openList.add(next);
                        nodeList.add(next);
                    }
                }
            }
        }
    }
 }

    void bfs(){    //bfs算法
        Start.setUp3();
        Start.path.add(Start);
        queue.add(Start);
        while(!queue.isEmpty()){
            Node best=queue.get(0);
            queue.remove(0);
            if(best.isTarget(Target)){        //判断是否为目标状态
                System.out.println("-------打印路径------");
                for(int i=0;i<best.path.size();i++){
                    System.out.println("第"+i+"次移动");
                    best.path.get(i).print();
                }
                System.out.println("共扩展了"+nodeList.size()+"个节点");
                return;
            }
            for(int i=0;i<4;i++){
                Node next=getNext(best,i);
                if(next!=null){       //是否可以移动到下一个状态
                    next.setParent(best);
                    next.setUp3();
                    next.path.add(next);
                    queue.add(next);
                    queue.add(next);
                }
            }
        }
    }

     void printPath(Node end){    //打印路径
          while(end!=null){
              path.add(end);
              end=end.getParent();
          }
          for(int i=0;i<path.size();i++){
              System.out.println("---------第"+(i+1)+"次移动--------");
               path.get(i).print();
              System.out.println("-------------------------");
          }
         System.out.println("移动次数:"+path.size());
     }
    public static void main(String[] args) {
        Astar astar=new Astar();
    }
}





class Node {       //用于定义状态的类
    private int N=3;
    int state[][]=new int[3][3];
    private int f;    //估计函数
    private int g;    //当前深度
    private int h;     //目标的估计
    private Node parent;  //存储当前结点的上一个状态
    List<Node> path=new ArrayList<>();   //存储路径
    public Node(){

    }

    public void setUp(Node target) {   //估价函数一
        int num=0;
        for(int i=0;i<3;i++){
            for(int j=0;j<3;j++)
            if(state[i][j]!=target.getState()[i][j]){
                num++;
            }
        }
        this.h = num;
        if(this.parent==null){
            this.g=0;
        }else{
            this.g=this.parent.getG()+1;
        }
        this.f=this.g+this.h;
    }
    public void setUp2(Node target,Map<Integer,int[]> map){   //估价函数二
        int num = 0;
        for (int row = 0; row < N; row++) {
            for (int cow = 0; cow < N; cow++) {
                if (cow != 0 && state[row][cow] != target.getState()[row][cow]){
                    num += Math.abs(row - map.get(state[row][cow])[0]) + Math.abs(cow - map.get(state[row][cow])[1]);
                }
            }
        }
        this.h = num;
        if(this.parent==null){
            this.g=0;
        }else{
            this.g=this.parent.getG()+1;
        }
        this.f=this.g+this.h;
    }
    public void setUp3(){            //bfs的估价函数
        this.h = 0;
        if(this.parent==null){
            this.g=0;
        }else{
            this.g=this.parent.getG()+1;
        }
        this.f=this.g+this.h;
    }

    public int[][] getState() {
        return state;
    }

    public void setState(int[][] state) {
        this.state = state;
    }

    public int getF() {
        return f;
    }

    public void setF(int f) {
        this.f = f;
    }

    public int getG() {
        return g;
    }

    public void setG(int g) {
        this.g = g;
    }

    public Node getParent() {
        return parent;
    }

    public void setParent(Node parent) {
        this.parent = parent;
    }

    public List<Node> getPath() {
        return path;
    }

    public void setPath(List<Node> path) {
        this.path = path;
    }

    public boolean isTarget(Node target){
        int i = 0,j=0;
        for (i = 0; i <N; i++) {
            for(j=0;j<N;j++) {
                if (state[i][j]!= target.getState()[i][j])
                    return false;
            }
        }
        return true;
    }

    public int[] getZeroIndex(){     //获得0的位置
        int x0 = 0, y0 = 0;
        for (x0 = 0; x0 < N; x0++) {
            boolean flag = false;
            for (y0 = 0; y0 < N; y0++) {
                if (state[x0][y0] == 0) {
                    flag = true;
                    break;
                }
            }
            if (flag)
                break;
        }
        return new int[]{x0, y0};
    }


   public void print(){    //打印函数
        for(int i=0;i<3;i++){
           for(int j=0;j<3;j++){
               System.out.print(state[i][j]+" ");
           }
            System.out.println();
        }
   }
}




public class Test(){
	 public static void main(String[] args) {
        Astar astar=new Astar();
    }
}

6.结果

使用0代替空格的位置，并输出打印路径和移动次数
比较两种不同的估计函数的结果值
设定初始状态为
2 8 3
1 6 4
7 0 5
目标状态为
1 2 3
8 0 4
7 6 5

不同估价函数的比较

搜索方法	扩展节点数
A*算法的估价函数一	14
A*算法的估价函数二	12
广度优先搜索(BFS)	684

对比来看不同的估价函数是能够影响搜索效率的，bfs的效率相比于A*算法是低了很多的。