UA MATH571A 一元线性回归III 方差分析与相关性分析
UA MATH571A 一元线性回归III 方差分析与相关性分析
- ANOVA Table
- F检验
- 回归系数的F检验
- F检验与t检验等价
- 广义线性检验方法
- R 2 R^2 R2
- 数值例子:女性肌肉量与年龄的关系
- 相关性系数
- PPMCC
- PPMCC的区间估计
- Spearman秩相关系数
- 数值例子:学历与犯罪率
ANOVA Table
ANOVA(Analysis of Variance)是分析方差构成的常用方法。在前两篇中,我们定义过
S S T = ∑ i = 1 N ( Y i − Y ˉ ) 2 SST = \sum_{i=1}^N (Y_i-\bar{Y})^2 SST=i=1∑N(Yi−Yˉ)2
SST表示被解释变量Y的样本总离差平方和(或称总平方和),代表样本数据整体的信息含量,其自由度为 d f T = N − 1 df_T=N-1 dfT=N−1。我们也定义过
S S E = ∑ i = 1 N e i 2 = ∑ i = 1 N ( Y i − Y ^ i ) 2 SSE = \sum_{i=1}^{N} e_i^2 = \sum_{i=1}^{N} (Y_i - \hat{Y}_i)^2 SSE=i=1∑Nei2=i=1∑N(Yi−Y^i)2
SSE是回归的残差平方和,代表无法被变量X解释的那部分信息量,自由度为 d f E = N − 2 df_E=N-2 dfE=N−2。
S S T − S S E = ∑ i = 1 N [ ( Y i − Y ˉ ) 2 − ( Y i − Y ^ i ) 2 ] = ∑ i = 1 N [ Y ˉ 2 + Y i ^ 2 − 2 Y i ( Y ^ i − Y ˉ ) ] = ∑ i = 1 N [ Y ˉ 2 + Y i ^ 2 − 2 ( Y i − Y ˉ ) ( Y ^ i − Y ˉ ) ] = ∑ i = 1 N ( Y ^ i − Y ˉ ) 2 ≜ S S R SST-SSE=\sum_{i=1}^N [(Y_i-\bar{Y})^2-(Y_i - \hat{Y}_i)^2] \\ =\sum_{i=1}^N [\bar{Y}^2+\hat{Y_i}^2-2Y_i(\hat{Y}_i-\bar{Y})] \\ = \sum_{i=1}^N [\bar{Y}^2+\hat{Y_i}^2-2(Y_i-\bar{Y})(\hat{Y}_i-\bar{Y})] \\ =\sum_{i=1}^N (\hat{Y}_i - \bar{Y})^2 \triangleq SSR SST−SSE=i=1∑N[(Yi−Yˉ)2−(Yi−Y^i)2]=i=1∑N[Yˉ2+Yi^2−2Yi(Y^i−Yˉ)]=i=1∑N[Yˉ2+Yi^2−2(Yi−Yˉ)(Y^i−Yˉ)]=i=1∑N(Y^i−Yˉ)2≜SSR
SSR是回归平方和,代表回归模型可以解释的那部分信息含量,自由度为 d f R = 1 df_R=1 dfR=1。对于回归而言,只有两个回归系数贡献两个自由度,但存在约束 ∑ i = 1 N ( Y ^ i − Y ˉ ) = 0 \sum_{i=1}^N (\hat{Y}_i - \bar{Y})=0 ∑i=1N(Y^i−Yˉ)=0,所以减去一个自由度,只剩下一个自由度。将三个平方和做自由度修正,定义
M S T = S S T d f T , M S R = S S R d f R , M S E = S S E d f E MST = \frac{SST}{df_T}, \ \ MSR = \frac{SSR}{df_R}, \ \ MSE = \frac{SSE}{df_E} MST=dfTSST, MSR=dfRSSR, MSE=dfESSE
根据上述定义,可以写出下列方差分析表(ANOVA Table)
| 来源 | SS | df | MS |
|---|---|---|---|
| 回归 | S S R = ∑ i = 1 N ( Y ^ i − Y ˉ ) 2 SSR=\sum_{i=1}^N (\hat{Y}_i - \bar{Y})^2 SSR=∑i=1N(Y^i−Yˉ)2 | 1 | M S R = S S R d f R MSR = \frac{SSR}{df_R} MSR=dfRSSR |
| 残差 | S S E = ∑ i = 1 N ( Y i − Y ^ i ) 2 SSE=\sum_{i=1}^N (Y_i - \hat{Y}_i )^2 SSE=∑i=1N(Yi−Y^i)2 | N-2 | M S E = S S E d f E MSE = \frac{SSE}{df_E} MSE=dfESSE |
| 总平方和 | S S T = ∑ i = 1 N ( Y i − Y ˉ ) 2 SST=\sum_{i=1}^N (Y_i - \bar{Y})^2 SST=∑i=1N(Yi−Yˉ)2 | N-1 | M S T = S S T d f T MST = \frac{SST}{df_T} MST=dfTSST |
F检验
回归系数的F检验
之前有说过MSE是方差的无偏估计,也就是 E ( M S E ) = σ 2 E(MSE)=\sigma^2 E(MSE)=σ2。现在计算一下MSR的期望。
S S R = ∑ i = 1 N ( Y ^ i − Y ˉ ) 2 = ∑ i = 1 N [ β ^ 0 + β ^ 1 X i − ( β ^ 0 + β ^ 1 X ˉ ) ] 2 = β ^ 1 2 ∑ i = 1 N ( X i − X ˉ ) 2 E ( β ^ 1 2 ) = V a r ( β ^ 1 ) + [ E ( β ^ 1 ) ] 2 = σ 2 ∑ i = 1 N ( X i − X ˉ ) 2 + β 1 2 E ( M S R ) = E ( S S R ) = σ 2 + β 1 2 ∑ i = 1 N ( X i − X ˉ ) 2 SSR = \sum_{i=1}^N (\hat{Y}_i - \bar{Y})^2 = \sum_{i=1}^N [\hat{\beta}_0 +\hat{\beta}_1X_i- (\hat{\beta}_0+\hat{\beta}_1\bar{X})]^2 =\hat{\beta}_1^2\sum_{i=1}^N (X_i - \bar{X})^2 \\ E(\hat{\beta}_1^2)=Var(\hat{\beta}_1)+[E(\hat{\beta}_1)]^2=\frac{\sigma^2}{\sum_{i=1}^N (X_i - \bar{X})^2} + \beta_1^2 \\ E(MSR)=E(SSR)=\sigma^2 + \beta_1^2 \sum_{i=1}^N (X_i - \bar{X})^2 SSR=i=1∑N(Y^i−Yˉ)2=i=1∑N[β^0+β^1Xi−(β^0+β^1Xˉ)]2=β^12i=1∑N(Xi−Xˉ)2E(β^12)=Var(β^1)+[E(β^1)]2=∑i=1N(Xi−Xˉ)2σ2+β12E(MSR)=E(SSR)=σ2+β12i=1∑N(Xi−Xˉ)2
显然当 β 1 \beta_1 β1等于0时,MSR也是方差的无偏估计,当 β 1 \beta_1 β1不等于0时,MSR不是方差的无偏估计。考虑对系数的双边检验:
H 0 : β 1 = 0 H a : β 1 ≠ 0 H_0: \beta_1 = 0 \\ H_a: \beta_1 \ne 0 H0:β1=0Ha:β1=0
定义统计量
F ∗ = M S R M S E F^* = \frac{MSR}{MSE} F∗=MSEMSR
S S R / σ 2 SSR/\sigma^2 SSR/σ2是标准正态随机变量的平方,由于自由度为1,因此服从 χ 2 ( 1 ) \chi^2(1) χ2(1)分布,所以根据F分布的定义,在原假设下, F ∗ ∼ ( 1 , N − 2 ) F^* \sim (1,N-2) F∗∼(1,N−2)。假设检验水平为 α \alpha α,若 F ∗ ≤ F ( 1 − α ; 1 , N − 2 ) F^*\le F(1-\alpha;1,N-2) F∗≤F(1−α;1,N−2),接受原假设,若 F ∗ > F ( 1 − α ; 1 , N − 2 ) F^*>F(1-\alpha;1,N-2) F∗>F(1−α;1,N−2),拒绝原假设。
F检验与t检验等价
F检验与双边t检验等价,
F ∗ = M S R M S E = S S R / 1 M S E = β ^ 1 2 ∑ i = 1 N ( X i − X ˉ ) 2 M S E = β ^ 1 2 s 2 { β ^ 1 } = ( t ∗ ) 2 F^* = \frac{MSR}{MSE}=\frac{SSR/1}{MSE}=\frac{\hat{\beta}_1^2\sum_{i=1}^N (X_i - \bar{X})^2}{MSE}=\frac{\hat{\beta}_1^2}{s^2\{\hat{\beta}_1\}}=(t^*)^2 F∗=MSEMSR=MSESSR/1=MSEβ^12∑i=1N(Xi−Xˉ)2=s2{β^1}β^12=(t∗)2
但由于F分布是单尾分布,因此与t检验不同,F检验只能做双边检验。
广义线性检验方法
完整的一元线性回归模型为FM(Full Model):
Y i = β 0 + β 1 X i + ϵ i Y_i = \beta_0 + \beta_1 X_i + \epsilon_i Yi=β0+β1Xi+ϵi
其残差平方和为
S S E ( F M ) = ∑ i = 1 N ( Y i − Y ^ i ) 2 = ∑ i = 1 N [ Y i − ( β ^ 0 + β ^ 1 X ^ i ) ] 2 = S S E SSE(FM)=\sum_{i=1}^N (Y_i - \hat{Y}_i )^2 = \sum_{i=1}^N [Y_i -( \hat{\beta}_0 + \hat{\beta}_1\hat{X}_i )]^2 =SSE SSE(FM)=i=1∑N(Yi−Y^i)2=i=1∑N[Yi−(β^0+β^1X^i)]2=SSE
在原假设下, β 1 \beta_1 β1等于0,完整的一元回归模型可以被简化为RM(Reduced Model):
Y i = β 0 + ϵ i Y_i = \beta_0 + \epsilon_i Yi=β0+ϵi
残差平方和为
S S E ( R M ) = ∑ i = 1 N ( Y i − Y ^ i ) 2 = ∑ i = 1 N ( Y i − β ^ 0 ) 2 = ∑ i = 1 N ( Y i − Y ˉ ) 2 = S S T SSE(RM)=\sum_{i=1}^N (Y_i - \hat{Y}_i )^2 = \sum_{i=1}^N (Y_i - \hat{\beta}_0 )^2 = \sum_{i=1}^N (Y_i - \bar{Y})^2 =SST SSE(RM)=i=1∑N(Yi−Y^i)2=i=1∑N(Yi−β^0)2=i=1∑N(Yi−Yˉ)2=SST
在这些设定下,可以将F检验推广。定义
F ∗ = S S E ( R M ) − S S E ( F M ) d f R M − d f F M / S S E ( F M ) d f F M ∼ F ( d f R M − d f F M , d f F M ) F^* = \frac{SSE(RM)-SSE(FM)}{df_{RM}-df_{FM}}/\frac{SSE(FM)}{df_{FM}} \sim F(df_{RM}-df_{FM},df_{FM}) F∗=dfRM−dfFMSSE(RM)−SSE(FM)/dfFMSSE(FM)∼F(dfRM−dfFM,dfFM)
原假设为应该使用RM,备择假设为应该使用FM。
R 2 R^2 R2
R 2 R^2 R2表示能够用回归模型解释的那部分信息占总信息的比值,
R 2 = S S R S S T = 1 − S S E S S T R^2 = \frac{SSR}{SST}=1-\frac{SSE}{SST} R2=SSTSSR=1−SSTSSE
R 2 R^2 R2又叫可决系数, R 2 R^2 R2越大代表回归模型越能解释被解释变量Y的变化情况,回归模型质量就越高。
数值例子:女性肌肉量与年龄的关系
我们最后再用这个例子来介绍一下做ANOVA的F检验的方法,关于这个例子已经完成的分析可以看前两篇博文。对线性模型lm()的输出结果使用anova()函数可以得到ANOVA Table,
> anova(Ex1.lm)
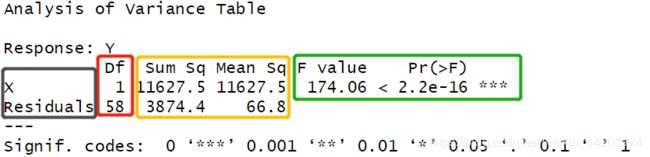
灰框中是ANOVA Table中的方差来源栏,红框中是自由度,黄框中是SS和MS。绿框中是F统计量和F检验的p值,根据这两个值可以判断回归系数 β 1 \beta_1 β1是显著异于0的,说明回归有效,这与t检验的结果一致。在回归结果的汇总中,

红框内的是F统计量及其对应的自由度,黄框内是F检验的p值,这与ANOVA Table中的结果一致。简单计算可以发现 β 1 \beta_1 β1的t统计量的平方等于F统计量,但t统计量可以有正负,而F统计量总是为正的,这是因为t分布是双尾分布,而F分布只有单尾。因此做单边检验时只能用t检验。蓝框内的值是 R 2 R^2 R2,这个值说明年龄可以解释女性肌肉量75%的变化。但要注意的是解释不代表因果,只是一个统计相关性。这个结果只能说明女性肌肉量的下降从统计上讲有75%与年龄增长有关,但不能证明女性肌肉量的下降有75%是年龄增长造成的。
相关性系数
在回归模型中,我们认为变量X的改变会引起变量Y的改变(称这种关系是统计上的因果关系),变量X被视为是常量,变量Y是随机变量。但在有的情况下,两个变量之间到底谁引起谁的改变很难说清楚,在这个时候可以做相关性分析(Correlation Analysis)分析两个变量的相关性而非统计因果,即假设待分析的两个变量均是随机变量。
假设 Y 1 Y_1 Y1与 Y 2 Y_2 Y2是两个随机变量,他们的相关性系数(Correlation Coefficients)为:
ρ = C o r r ( Y 1 , Y 2 ) = C o v ( Y 1 , Y 2 ) V a r ( Y 1 ) V a r ( Y 2 ) \rho=Corr(Y_1,Y_2)=\frac{Cov(Y_1,Y_2)}{\sqrt{Var(Y_1)Var(Y_2)}} ρ=Corr(Y1,Y2)=Var(Y1)Var(Y2)Cov(Y1,Y2)
二元相关性分析的目标是估计这个相关性系数,并检验这个系数是否为零(双边检验)或者检验系数的符号(单边检验)。通常假设这两个变量服从二元正态分布,概率密度函数如下:
f ( y 1 , y 2 ) = 1 2 π σ 1 σ 2 1 − ρ 2 e x p { − 1 2 ( 1 − ρ 2 ) [ ( Y 1 − μ 1 σ 1 ) 2 − 2 ρ ( Y 1 − μ 1 σ 1 ) ( Y 2 − μ 2 σ 2 ) + ( Y 2 − μ 2 σ 2 ) 2 ] } f(y_1,y_2)=\frac{1}{2 \pi \sigma_1 \sigma_2 \sqrt{1-\rho^2}}exp\{ -\frac{1}{2(1-\rho^2)} [(\frac{Y_1-\mu_1}{\sigma_1})^2 - 2\rho (\frac{Y_1-\mu_1}{\sigma_1}) (\frac{Y_2-\mu_2}{\sigma_2})+ (\frac{Y_2-\mu_2}{\sigma_2})^2] \} f(y1,y2)=2πσ1σ21−ρ21exp{−2(1−ρ2)1[(σ1Y1−μ1)2−2ρ(σ1Y1−μ1)(σ2Y2−μ2)+(σ2Y2−μ2)2]}
但这个表达式真的很长,定义 Y = [ Y 1 , Y 2 ] T Y=[Y_1,Y_2]^T Y=[Y1,Y2]T, μ = [ μ 1 , μ 2 ] T \mu=[\mu_1,\mu_2]^T μ=[μ1,μ2]T,
Σ = { σ 1 2 ρ σ 1 σ 2 ρ σ 1 σ 2 σ 2 2 } \Sigma= \left\{ \begin{matrix} \sigma_1^2 & \rho \sigma_1 \sigma_2 \\ \rho \sigma_1 \sigma_2 & \sigma_2^2\\ \end{matrix} \right\} \\ Σ={σ12ρσ1σ2ρσ1σ2σ22}
可以将分布记作 Y ∼ N ( μ , Σ ) Y \sim N(\mu, \Sigma) Y∼N(μ,Σ),概率密度函数可以写成:
f ( Y ) = 1 ( 2 π ) n / 2 d e t Σ e x p [ − 1 2 ( Y − μ ) T Σ − 1 ( Y − μ ) ] f(Y)=\frac{1}{(2 \pi)^{n/2}\sqrt{det \Sigma}} exp[-\frac{1}{2} (Y-\mu)^T \Sigma^{-1}(Y-\mu)] f(Y)=(2π)n/2detΣ1exp[−21(Y−μ)TΣ−1(Y−μ)]
假设现在我们有一组样本 { ( Y 1 i , Y 2 i ) } i = 1 N \{(Y_{1i},Y_{2i})\}_{i=1}^{N} {(Y1i,Y2i)}i=1N,用最大似然法:
L ( μ , Σ ) = f ( ( Y 1 i , Y 2 i ) i = 1 N ∣ μ , Σ ) = ∏ i = 1 N f ( Y 1 i , Y 2 i ) l ( μ , Σ ) = ∑ i = 1 N l n f ( Y 1 i , Y 2 i ) = − 1 2 ( 1 − ρ 2 ) ∑ i = 1 N { [ ( Y 1 − μ 1 σ 1 ) 2 − 2 ρ ( Y 1 − μ 1 σ 1 ) ( Y 2 − μ 2 σ 2 ) + ( Y 2 − μ 2 σ 2 ) 2 ] } − N l n ( 2 π σ 1 σ 2 1 − ρ 2 ) L(\mu,\Sigma)=f({(Y_{1i},Y_{2i})}_{i=1}^{N}|\mu,\Sigma)=\prod_{i=1}^{N} f(Y_{1i},Y_{2i}) \\ l(\mu,\Sigma) = \sum_{i=1}^{N} lnf(Y_{1i},Y_{2i})= -\frac{1}{2(1-\rho^2)} \sum_{i=1}^{N} \{ [(\frac{Y_1-\mu_1}{\sigma_1})^2 - 2\rho (\frac{Y_1-\mu_1}{\sigma_1}) (\frac{Y_2-\mu_2}{\sigma_2})+ (\frac{Y_2-\mu_2}{\sigma_2})^2] \} - Nln(2 \pi \sigma_1 \sigma_2 \sqrt{1-\rho^2}) L(μ,Σ)=f((Y1i,Y2i)i=1N∣μ,Σ)=i=1∏Nf(Y1i,Y2i)l(μ,Σ)=i=1∑Nlnf(Y1i,Y2i)=−2(1−ρ2)1i=1∑N{[(σ1Y1−μ1)2−2ρ(σ1Y1−μ1)(σ2Y2−μ2)+(σ2Y2−μ2)2]}−Nln(2πσ1σ21−ρ2)
最大化对数似然,即可求解出五个参数的最大似然估计。尽管形式有点复杂,但过程非常标准化。
PPMCC
PPMCC全称是Pearson交叉矩相关性系数(Pearson Product-Moment Correlation Coefficients),是相关性系数的最大似然估计:
r 12 = ∑ ( Y 1 i − Y ˉ 1 ) ( Y 2 i − Y ˉ 2 ) ∑ ( Y 1 i − Y ˉ 1 ) 2 ∑ ( Y 2 i − Y ˉ 2 ) 2 r_{12}=\frac{\sum (Y_{1i}-\bar{Y}_1) (Y_{2i}-\bar{Y}_2)}{\sqrt{ \sum (Y_{1i}-\bar{Y}_1)^2 \sum (Y_{2i}-\bar{Y}_2)^2 }} r12=∑(Y1i−Yˉ1)2∑(Y2i−Yˉ2)2∑(Y1i−Yˉ1)(Y2i−Yˉ2)
但这个估计量并不是相关性系数的无偏估计,有兴趣的读者可以自己推一下。相关性分析可以看成是做如下检验:
H 0 : ρ = 0 H a : ρ ≠ 0 H_0: \rho=0\\ H_a: \rho \ne 0 H0:ρ=0Ha:ρ=0
下面我们推导这个检验要怎么做。由于二元正态分布的边缘分布仍然是正态分布,所以 Y 1 Y_1 Y1的边缘密度为
f ( y 1 ) = 1 2 π σ 1 e x p { − ( Y 1 − μ 1 ) 2 σ 2 } f(y_1)=\frac{1}{\sqrt{2 \pi}\sigma_1} exp\{-\frac{(Y_1-\mu_1)}{2\sigma^2}\} f(y1)=2πσ11exp{−2σ2(Y1−μ1)}
Y 2 Y_2 Y2关于 Y 1 Y_1 Y1的条件密度为
f ( y 2 ∣ y 1 ) = 1 2 π ( 1 − ρ 2 ) σ 2 e x p { − ( Y 2 − μ 2 + μ 1 ρ σ 2 σ 1 − ρ σ 2 σ 1 Y 1 ) 2 σ 2 2 ( 1 − ρ 2 ) } f(y_2|y_1)=\frac{1}{\sqrt{2 \pi (1-\rho^2)}\sigma_2 } exp\{-\frac{(Y_2-\mu_2+\mu_1 \rho \frac{\sigma_2}{\sigma_1} - \rho \frac{\sigma_2}{\sigma_1} Y_1)}{2\sigma_2^2 (1-\rho^2)}\} f(y2∣y1)=2π(1−ρ2)σ21exp{−2σ22(1−ρ2)(Y2−μ2+μ1ρσ1σ2−ρσ1σ2Y1)}
定义:
α 2 ∣ 1 = μ 2 − μ 1 ρ σ 2 σ 1 β 21 = ρ σ 2 σ 1 σ 2 ∣ 1 = σ 2 2 ( 1 − ρ 2 ) \alpha_{2|1} = \mu_2-\mu_1 \rho \frac{\sigma_2}{\sigma_1} \\ \beta_{21} =\rho \frac{\sigma_2}{\sigma_1} \\ \sigma_{2|1} = \sigma_2^2 (1-\rho^2) α2∣1=μ2−μ1ρσ1σ2β21=ρσ1σ2σ2∣1=σ22(1−ρ2)
从而 E ( Y 2 ∣ Y 1 ) = α 2 ∣ 1 + β 21 Y 1 E(Y_2 | Y_1) = \alpha_{2|1} + \beta_{21} Y_1 E(Y2∣Y1)=α2∣1+β21Y1,在原假设下, β 21 = 0 \beta_{21}=0 β21=0,将 β 21 \beta_{21} β21视为 Y 2 ∣ Y 1 Y_2|Y_1 Y2∣Y1关于 Y 1 Y_1 Y1的回归系数,上面的检验可以视为:
H 0 : β 21 = 0 H a : β 21 ≠ 0 H_0: \beta_{21}=0\\ H_a: \beta_{21} \ne 0 H0:β21=0Ha:β21=0
构造t统计量
t ∗ = β ^ 21 s e ( β 21 ^ ) = r 12 N − 2 1 − r 12 2 ∼ t ( N − 2 ) t^* = \frac{\hat{\beta}_{21} }{se(\hat{\beta_{21}})} =\frac{r_{12}\sqrt{N-2}}{\sqrt{1-r_{12}^2}} \sim t(N-2) t∗=se(β21^)β^21=1−r122r12N−2∼t(N−2)
基于该统计量可以完成对PPMCC的假设检验。
PPMCC的区间估计
因为PPMCC的分布在原假设不成立时非常复杂,因此采用下面的方法计算置信区间。对PPMCC做Fisher z变换:
z = 1 2 l n ( 1 + r 12 1 − r 12 ) z = \frac{1}{2}ln(\frac{1+r_{12}}{1-r_{12}}) z=21ln(1−r121+r12)
不加证明地给出下列结果:当N足够大时(一般 N > 25 N>25 N>25即可),有以下渐进分布
z ∼ N ( 1 2 l n ( 1 + ρ 2 1 − ρ 2 ) , 1 N − 3 ) z \sim N(\frac{1}{2}ln(\frac{1+\rho^2}{1-\rho^2}),\frac{1}{N-3}) z∼N(21ln(1−ρ21+ρ2),N−31)
由此可以构造Z统计量:
z − 1 2 l n ( 1 + ρ 2 1 − ρ 2 ) 1 / N − 3 ∼ N ( 0 , 1 ) \frac{z- \frac{1}{2}ln(\frac{1+\rho^2}{1-\rho^2})}{1/\sqrt{N-3}} \sim N(0,1) 1/N−3z−21ln(1−ρ21+ρ2)∼N(0,1)
并可据此计算置信区间。
Spearman秩相关系数
当 Y 1 Y_1 Y1和 Y 1 Y_1 Y1不服从二元正态分布时,可以考虑将其变换成二元正态分布。但当很难找到合适的变换时,我们就不能使用上面的方法做相关性分析了。在 Y 1 Y_1 Y1和 Y 2 Y_2 Y2的联合密度未知或者比较复杂的时候可以考虑使用非参数方法。对于 Y 1 Y_1 Y1的一列观测值 { Y 11 , Y 21 , . . . , Y N 1 } \{Y_{11},Y_{21}, ... , Y_{N1}\} {Y11,Y21,...,YN1},假设 Y i 1 Y_{i1} Yi1按从大到小排第k个( k = 1 , 2 , . . . , N k=1,2,...,N k=1,2,...,N),记 R i 1 = k R_{i1}=k Ri1=k为第i个观察值的秩(rank)。对于 Y 1 Y_1 Y1和 Y 2 Y_2 Y2观测值的秩,定义Spearman秩相关系数(Spearman Rank Correlation Coefficients):
r S = ∑ ( R 1 i − R ˉ 1 ) ( R 2 i − R ˉ 2 ) ∑ ( R 1 i − R ˉ 1 ) 2 ∑ ( R 2 i − R ˉ 2 ) 2 r_S = \frac{\sum (R_{1i}-\bar{R}_1) (R_{2i}-\bar{R}_2)}{\sqrt{ \sum (R_{1i}-\bar{R}_1)^2 \sum (R_{2i}-\bar{R}_2)^2 }} rS=∑(R1i−Rˉ1)2∑(R2i−Rˉ2)2∑(R1i−Rˉ1)(R2i−Rˉ2)
其中 R ˉ 1 = R ˉ 2 = N + 1 2 \bar{R}_1=\bar{R}_2=\frac{N+1}{2} Rˉ1=Rˉ2=2N+1。同样考虑如下检验:
H 0 : ρ = 0 H a : ρ ≠ 0 H_0: \rho=0\\ H_a: \rho \ne 0 H0:ρ=0Ha:ρ=0
不加证明地给出统计量:
t ∗ = r S N − 2 1 − r S 2 ∼ t ( N − 2 ) t^* =\frac{r_{S}\sqrt{N-2}}{\sqrt{1-r_{S}^2}} \sim t(N-2) t∗=1−rS2rSN−2∼t(N−2)
只要 N > 10 N>10 N>10就可认为上述统计量的渐进分布成立,并进行相关性分析。
数值例子:学历与犯罪率
这个例子的数据来源于Applied Linear Regression Models. Kutner et al 第一章二十八题。一项犯罪学的研究想要探索教育与犯罪率之间的关系,于是随机选取了84个中等规模的社区,并收集了社区居民持高中文化以上的人数占(Y2)以及社区犯罪率(Y1)。从直觉上讲,学历越高的社区居民素质越高,犯罪率就会越低。因此做假设检验:
H 0 : ρ ≥ 0 H a : ρ < 0 H_0: \rho \ge 0\\ H_a: \rho < 0 H0:ρ≥0Ha:ρ<0
先读取数据,由于犯罪率的数据是每十万人的犯罪次数,所以这里用犯罪率除以10万得到犯罪率
## Set work dictionary
setwd("D:\\Stat PhD\\semester1\\regression\\Notes\\Ch2")
## Read-in text data
Ex2 <- read.table("D:/Stat PhD/semester1/regression/Notes/Ch2/CH01PR28.txt", quote="\"", comment.char="")
Ex2 <- as.matrix(Ex2)
Y1 <- Ex2[,1]/100000
Y2 <- Ex2[,2]
假设检验水平为5%,用PPMCC做相关性分析
> alpha <- .05
> N <- length(Y1)
> r12 <- cor(Y1,Y2)
> r12
[1] -0.4127033
> t <- r12*sqrt(N-2)/sqrt(1-r12^2)
> t
[1] -4.102897
> t < -qt(1-alpha/2,N-2)
[1] TRUE
> p <- pt(t,N-2)
> p
[1] 4.785698e-05
PPMCC的估计值是-0.4127033,t检验统计量的值为-4.102897,小于 t ( 1 − α / 2 , N − 2 ) t(1-\alpha/2,N-2) t(1−α/2,N−2),这说明社区居民的学历与犯罪率呈显著的负相关。该检验的p值为0.00004785698。我们还可以计算出相关性系数的95%置信区间,为[-0.5761223,-0.217558],显然95%置信区间在负半轴,说明t统计量整体分布都集中在负半轴。
> z = 0.5*( log(1+r12) - log(1-r12) )
> se = 1/sqrt( N-3 )
> zlwr = z - qnorm( 1-alpha/2 )*se
> zupr = z + qnorm( 1-alpha/2 )*se
> rholwr = (exp(2*zlwr)-1)/(exp(2*zlwr)+1)
> rhoupr = (exp(2*zupr)-1)/(exp(2*zupr)+1)
> c(rholwr, rhoupr)
[1] -0.5761223 -0.2175580
用Spearman秩相关做相关性分析。
> cor.test(Y1,Y2,method = "spearman",exact = F)
Spearman's rank correlation rho
data: Y1 and Y2
S = 140839, p-value = 5.359e-05
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
-0.4259324
Spearman秩相关系数为-0.4259324,与PPMCC还是比较接近的,检验结果是接受备择假设,二者显著负相关,p值为5.539e-5。综合上面的分析,可以初步认为社区居民犯罪率与学历是负相关的。