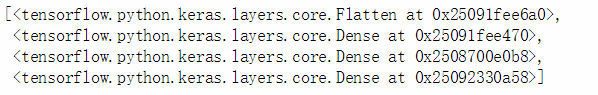TensorFlow学习笔记（二）分类模型构建
这里一枚小白，啥也不会，请多指正(´-ι_-｀)
一、两大类问题
1. 回归问题：预测的为值，模型输出的为实数值。如：预测房价。
2. 分类问题：预测的为类别，模型输出的为概率分布。
如：三分类问题输出例子：[0.2,0.7,0.1]。
- 每个位置的代表一个类别。如上，三个位置即表示其为三分类问题。
- 第0个位置输出的概率为0.2，表示该样本为第0类的概率为0.2；第1个位置输出的概率为0.7，表示该样本为第1类的概率为0.7；第2个位置输出的概率为0.1，表示该样本为第2类的概率为0.1。
- 0.2+0.7+0.1=1，即满足概率和为1。
- 预测的类别就是概率最大的那个类。如上，该例子预测样本为第1类。
二、目标函数
1. 目标函数的作用：衡量构建的模型的好坏。（注：模型的参数是逐步调整的。)
2. 对于分类问题，目标函数需要衡量目标类别与当前预测的差距。
如：三分类问题输出例子：预测值的分布为[0.2,0.7,0.1]，模型预测样本为第1类。但假设实际目标类别（真实类别）为第2类，则三分类的真实类别的表示为 2。将 2 经过one_hot编码，生成1个长度为3的向量（第2个位置是1，其余位置都是0 ），即 2 → one_hot → [0,0,1] ，则[0,0,1]即为真实值的分布。
注： One_hot编码：用于把正整数变为向量表达。输入为正整数，输出为1个长度不小于正整数的向量。而在分类问题上，one_hot 会生出1个只有在正整数位置处为1，其余位置均为0的向量。
3. 分类问题中常见的两种目标函数：
- 平方差损失：
注： y和Model(x)都是向量，所以这里做的是一个向量的运算。
例：预测值：[0.2,0.7,0.1]；真实值：[0,0,1]；损失函数值（给预测值的分布和真实值的分布计算距离）： [(0.2-0)²+(0.7-0)²+(0.1-1)²] 0.5 = 0.67
- 交叉熵损失：
三、实战
1. 各种库的引入。
import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import sklearn
import pandas as pd
import os
import sys
import time
import tensorflow as tf
from tensorflow import keras
print(tf.__version__) #打印tensorflow的版本
print(sys.version_info)
for module in mpl,np,pd,sklearn,tf,keras:
print(module.__name__,module.__version__)输出结果为（根据安装的版本不同会有不同）：
2. 导入1个关于分类问题的数据集。
"""对于分类问题，导入一个分类问题的数据集。在keras中有一定的数据集。"""
fashion_mnist = keras.datasets.fashion_mnist #导入数据集
"""mnist是手写数字的数据集。fashion_mnist中有一些黑白图像，可在keras.datasets中直接导入。"""
(x_train_all,y_train_all),(x_test,y_test) = fashion_mnist.load_data() #使用load_data函数把训练集和测试集都拆分出来
x_valid,x_train = x_train_all[:5000],x_train_all[5000:] #把训练集再次拆分为验证集和训练集
y_valid,y_train = y_train_all[:5000],y_train_all[5000:]
# 打印验证集、训练集和测试集的shape
print(x_valid.shape,y_valid.shape) #5000张图片，28*28的图像
print(x_train.shape,y_train.shape) #55000张图片，28*28的图像
print(x_test.shape,y_test.shape) #10000张图片，28*28的图像输出结果为：
3. 了解数据集。
#了解数据集
def show_single_image(img_arr): #定义一个“展示一张图像”函数
plt.imshow(img_arr,cmap="binary") #调用imshow
"""cmap="binary"定义的是颜色图谱，默认是rgb。这里的样本本身是黑白图片，rgb足以满足。"""
plt.show() # 调用show，显示图像
show_single_image(x_train[0])输出结果为：
4. 显示部分数据集。
def show_imgs(n_rows, n_cols, x_data, y_data, class_names): #定义函数show_imgs
"""函数show_imgs,可显示n行n列。显示图像一般有参数x_data即可，但是y_data可把图像的类别也显示出来。此外，还需定义一个类别名的输出。"""
#做一些验证
assert len(x_data) == len(y_data) #验证x的样本数和y的样本数是一样的
assert n_rows * n_cols 输出结果为：
5. 构建模型。
#tf.keras.models.Sequential()构建模型
"""在官网中对Sequential的介绍为"layers:list of layers to add to model."即将一系列的层次堆叠起来。"""
model = keras.models.Sequential() #创建一个Sequential的对象
model.add(keras.layers.Flatten(input_shape=[28,28])) #添加输入层，展开输入的图片
"""往这个Sequential对象里面添加层，首先添加的是输入层，这一层的作用：使用Flatten将输入的对象（1张28*28的图像）展平，即将1个28*28的二维矩阵展平成为1个一维向量。"""
model.add(keras.layers.Dense(300, activation="relu")) #添加全连接层，单元数为300
"""展平之后，再加入新的一层，这一层为全连接层（最普通的神经网络），并把上一层的所有单元都与下一层的所有单元进行一一连接。把这一层的单元数设为300，activation即为激活函数，设为"relu"。"""
model.add(keras.layers.Dense(100, activation="relu")) #添加全连接层，单元数为100
#这一层的100个单元就会和上一层300个单元进行全连接
model.add(keras.layers.Dense(10,activation="softmax")) #添加输出层，输出概率分布
"""再添加一层，控制其的输出。上述的问题是一个分类问题，模型输出应为长度为10的一个概率分布，这里应使其的输出为一个长度为10的向量。"""
"""
#Sequential函数的另一种写法，不用逐层调用add函数，可以将每层都放置在一个列表中：
model = keras.models.Sequential([keras.layers.Flatten(input_shape=[28,28]),
keras.layers.Dense(300, activation="relu"),
keras.layers.Dense(100, activation="relu"),
keras.layers.Dense(10, activation="softmax")])
效果与上相同。
"""
#有了概率分布之后，就可以计算目标函数
model.compile(loss = "sparse_categorical_crossentropy",
optimizer = "adam",
metrics = ["accuracy"])
"""
这个函数的参数分别为：
损失函数 loss，
"crossentropy"即为上述“交叉熵”的损失函数。加上前缀sparse的原因为：y → index。
放置损失函数的前提是：y → one_hot → []（向量）。因为这里的y长度等于样本数量，所以对于每个样本而言，y都是1个数值。若y为1个数值，则使用"sparse_categorical_crossentropy"；若y为1个向量，就无需使用"sparse"，直接使用"categorical_crossentropy"即可。
optimizer为目标函数的求解方法，调整参数，使目标函数越来越小，这里就是目标函数参数的调整方法。
除目标函数的指标之外，还应注意其他指标，如"accuracy"。
目的是将目标函数指标和其他我们关心的指标构建到图中。
"""2种激活函数如下：
- relu函数：
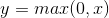，即输入一个x，输出是x与0的最大值。当x>0时，输出的y为x；当x<0时，输出的y为0。 - softmax函数：该函数将向量变成概率分布。
如：存在向量 ![[x1,x2,x3]](http://img.e-com-net.com/image/info8/cac54c22c9674180972f6ba551b2004d.gif){kind=small}
，转变为 ![y=[\frac{e^{x1}}{sum},\frac{e^{x2}}{sum},\frac{e^{x3}}{sum}]](http://img.e-com-net.com/image/info8/8416c3f1e2364a838b5366d184df162c.gif){kind=small}
，
。 这样就将向量变成了一个概率分布，因为y中的3个值的和为1，且都在0和1之间。
6. 查看模型中的层数。
model.layers # 可以看到我们构建的模型中有多少层输出结果为：
如上所示，正是构建的4层。
7. 通过model.summary()输出模型各层的参数状况。
model.summary()输出结果为：
Outshape：
第一层的 [None,784] （样本数为784的1个矩阵），变化为第二层的 [None,300] （样本数为300的1个矩阵）。
变化过程为： [None,784] * W（变化的方式是乘以一个矩阵）+ b（加一个偏置）= [None,300]
其中： W.shape为[784,300]，b=[300]（b为长度为300的一个向量） 所以第二层的参数量=784*300+300=235500（参数量的计算）。
8. 训练模型。
#构建好图以后，可以开启训练
history = model.fit(x_train, y_train, epochs=10,
#epochs表示命令这个训练集多少次，epochs=10表示命令这个训练集10次
validation_data=(x_valid,y_valid))
#每隔段时间，会对这个训练集做验证
#history表示model.fit返回的一个值，称为 数据结果输出结果为：
9. 查看history的变量类型。
type(history) #查看history变量类型：callbacks输出结果为：
10.
history.history #history中的一个变量，其中包含一些值输出结果为一些数值。
11. 打印出指标的变化过程。
#把这些指标的值的变化过程，用一张图打印出来
def plot_learning_curves(history):
pd.DataFrame(history.history).plot(figsize=(8, 5)) #DataFrame是一个重要的数据结构， figsize=(8,5)表示把图的大小设置为8和5
plt.grid(True) #显示网格
plt.gca().set_ylim(0,1) #设置坐标轴的范围，set_ylim(0,1)设置y轴坐标轴的范围
plt.show() #显示这张图
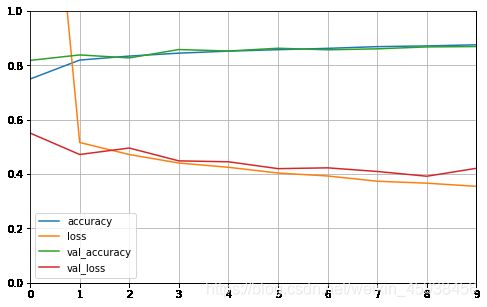
plot_learning_curves(history)输出结果为：
由输出结果所示，accuracy和val_accuracy呈稳步增长趋势，而loss和val_loss呈下降趋势。
如上就搭建了一个完整的分类模型，从数据处理到模型构建到模型训练，到指标图示的打印。