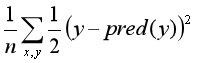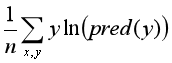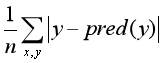一、tensorflow与tf.keras简介
tensorflow和keras及tf.keras的区别
API: 全称Application Programming Interface,即应用程序编程接口。API是一些预定义函数,目的是用来提供应用程序与开发人员基于某软件或者硬件得以访问一组例程的能力,并且无需访问源码或无需理解内部工作机制细节。
tensorflow: Google开源的基于数据流图的机器学习框架,支持python和c++程序开发语言。轰动一时的AlphaGo就是使用tensorflow进行训练的,其命名基于工作原理,tensor 意为张量(即多维数组),flow 意为流动。即多维数组从数据流图一端流动到另一端。目前该框架支持 Windows、Linux、Mac乃至移动手机端等多种平台。
Keras是基于TensorFlow和Theano(由加拿大蒙特利尔大学开发的机器学习框架)的深度学习库,是由纯python编写而成的高层神经网络API,是为了支持快速实践而对tensorflow或者Theano的再次封装。
区别:keras本身并不具备底层运算的能力,所以它需要和一个具备这种底层运算能力的backend(后端)协同工作。即keras为前端,tensorflow为keras常用的后端。
tf.keras是一个不强调后端可互换性、和tensorflow更紧密整合、得到tensorflow其他组建更好支持、且符合keras标准的高层次API。如今tf.keras版本和keras进行了同步,tf.keras作为官方的tensorflow的高级API。
二、分类与回归问题
分类问题预测的是类别,模型的输出是概率分布。
回归问题预测的是数值,模型输出的也是数值。
目标函数:用来衡量模型的好坏。
一、分类问题
1、需要衡量目标类别与当前预测的差距
eg. 三分类问题输出概率分布:[0.2, 0.7, 0.1],即预测为第0类,第一类或者第二类的概率分别为0.2,0.7,0.1。但在这里要做one-hot编码,即将真实的类别编码为1,其余编码为0。这里假如真实类别为第二类的话,输出概率分布经one-hot编码编码之后的结果为[0, 0, 1]。
2、损失函数
分类问题中常用的损失函数有:
- 平方差损失函数:
这里n为总的样本数,y为真实标签,pred(y)为通过模型预测的标签。
- 交叉熵损失函数:
二、回归问题
1、需要衡量预测值与真实值的差距
2、损失函数
分类问题中常用的损失函数有:
- 平方差损失函数
- 绝对值损失函数:
3、模型训练:通过调整参数,使得目标函数逐渐变小的过程
三、keras实战——搭建分类模型
新建python3文件——tf_keras_classification_model.py
一、首先import进所必须的模块,并查看版本号。
1 import matplotlib as mpl 2 import matplotlib.pyplot as plt 3 #%matplotlib inline 4 import numpy as np 5 import sklearn 6 import pandas as pd 7 8 import os 9 import sys 10 import time 11 import tensorflow as tf 12 from tensorflow import keras 13 14 print(tf.__version__) 15 print(sys.version_info) 16 17 for module in mpl,np,pd,sklearn,tf,keras: 18 print(module.__name__,module.__version__)
我们可以看到各模块的版本号分别为:
2.0.0 sys.version_info(major=3, minor=7, micro=4, releaselevel='final', serial=0) matplotlib 3.1.1 numpy 1.16.5 pandas 0.25.1 sklearn 0.21.3 tensorflow 2.0.0 tensorflow_core.keras 2.2.4-tf
二、然后我们导入keras中的fashion_mnist数据集并查看数据大小:
1 # 导入Keras中的数据 2 fashion_mnist = keras.datasets.fashion_mnist 3 (x_train_all,y_train_all),(x_test,y_test) = fashion_mnist.load_data() 4 5 # 将数据集拆分成训练集与验证集 6 # 将前5000张图片作为验证集,后55000张图片作为训练集 7 x_valid,x_train = x_train_all[:5000],x_train_all[5000:] 8 y_valid,y_train = y_train_all[:5000],y_train_all[5000:] 9 print(x_valid.shape,y_valid.shape) 10 print(x_train.shape,y_train.shape) 11 print(x_test.shape,y_test.shape)
打印结果为:
(5000, 28, 28) (5000,) (55000, 28, 28) (55000,) (10000, 28, 28) (10000,)
接下来我们可以简单了解下数据集中的内容:
1 def show_single_image(img): 2 plt.imshow(img,cmap='binary') 3 plt.show() 4 show_single_image(x_train[0])
我们可以看到训练集中的第一张图片:
当然我们也可以写个函数展示出多张图片:
1 def show_imgs(n_rows,n_cols,x_data,y_data,class_names): 2 assert len(x_data) == len(y_data) 3 assert n_rows * n_cols < len(x_data) 4 plt.figure(figsize = (n_cols * 1.4,n_rows * 1.6)) 5 for row in range(n_rows): 6 for col in range(n_cols): 7 index = n_cols * row + col 8 plt.subplot(n_rows,n_cols,index+1) 9 plt.imshow(x_data[index],cmap='binary',interpolation='nearest') 10 plt.axis('off') 11 plt.title(class_names[y_data[index]]) 12 plt.show() 13 14 class_names=['T-shirt','Trouser','Pullover','Dress','Coat','Sandal','Shirt','Sneaker','Bag','Ankle boot'] 15 show_imgs(4,5,x_train,y_train,class_names)
三、构建tf.keras模型
构建keras模型要用到 tf.keras.Sequential API (查看详细介绍www.tensorflow.org)。
方法一:用model.add方法
#方法一 model = keras.models.Sequential() #将输入的28*28的图像展平为784(28*28)的一维向量 model.add(keras.layers.Flatten(input_shape=[28,28])) #全连接层,输出长度为300,激活函数为‘relu’函数 model.add(keras.layers.Dense(300,activation='relu')) #全连接层,输出长度为100,激活函数为‘relu’函数 model.add(keras.layers.Dense(100,activation='relu')) #全连接层,因为我们这里是10个类别的分类问题,故输出长度为10,激活函数为‘softmax’函数 model.add(keras.layers.Dense(10,activation='softmax'))
方法二:
#方法二 model = keras.models.Sequential([ keras.layers.Flatten(input_shape=[28,28]), keras.layers.Dense(300,activation='relu'), keras.layers.Dense(100,activation='relu'), keras.layers.Dense(10,activation='softmax') ])
这样一来我们就搭建好了一个简单的模型,然后我们在配置学习过程,即设置损失函数、优化器和训练指标。代码如下:
#配置学习过程 model.compile(loss = 'sparse_categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
这里的loss意为损失函数,模型使用的是 'sparse_categorical_crossentropy',可以自动对 y_train 进行one-hot 编码。若 y_train 已经是编码后的数据了,则可以使用loss='categorical_crossentropy'
optimizer 为模型的求解方法,并依靠这个来调整参数, 模型使用的 ‘sgd’ 为随机梯度下降法。
metrics为我们还需关注的其他性能,这里是精度accuracy。
然后我们可以通过下述代码查看模型架构:
#查看模型概况(架构) model.summary()
代码运行结果如下:
Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= flatten (Flatten) (None, 784) 0 _________________________________________________________________ dense (Dense) (None, 300) 235500 _________________________________________________________________ dense_1 (Dense) (None, 100) 30100 _________________________________________________________________ dense_2 (Dense) (None, 10) 1010 ================================================================= Total params: 266,610 Trainable params: 266,610 Non-trainable params: 0 _________________________________________________________________
我们可以看到网络共有四层。
在这里涉及的参数(Param)个数的计算:以第二层dense为例,输入为(None, 784),经dense层来得到长度为300的结果(None, 300),其中None为样本数,具体过程为:
(None, 784)* W + b = (None, 300),这里的 W 为权重,b 为偏置,由矩阵相关知识我们可以知道 W 为(784,300),b 为(300,),所以总的参数个数为params=784*300+300=235500。
四、开启训练
#开启训练 history = model.fit(x_train,y_train,epochs=10, validation_data=(x_valid,y_valid)) #epochs为遍历数据集的次数
这里用 fit 方法来对模型进行训练,需要传入的参数包括:1、训练集,2、遍历次数epochs,3、验证集
训练过程为:
Train on 55000 samples, validate on 5000 samples Epoch 1/10 55000/55000 [==============================] - 9s 171us/sample - loss: 3032409856428.1016 - accuracy: 0.1002 - val_loss: 2.3028 - val_accuracy: 0.0914 Epoch 2/10 55000/55000 [==============================] - 8s 140us/sample - loss: 2.3027 - accuracy: 0.0993 - val_loss: 2.3028 - val_accuracy: 0.0914 Epoch 3/10 55000/55000 [==============================] - 8s 141us/sample - loss: 2.3026 - accuracy: 0.0999 - val_loss: 2.3028 - val_accuracy: 0.0986 Epoch 4/10 55000/55000 [==============================] - 8s 141us/sample - loss: 2.3026 - accuracy: 0.0986 - val_loss: 2.3029 - val_accuracy: 0.0976 Epoch 5/10 55000/55000 [==============================] - 8s 141us/sample - loss: 2.3026 - accuracy: 0.0994 - val_loss: 2.3027 - val_accuracy: 0.0976 Epoch 6/10 55000/55000 [==============================] - 8s 138us/sample - loss: 2.3027 - accuracy: 0.0994 - val_loss: 2.3028 - val_accuracy: 0.0980 Epoch 7/10 55000/55000 [==============================] - 8s 138us/sample - loss: 2.3027 - accuracy: 0.0991 - val_loss: 2.3028 - val_accuracy: 0.1000 Epoch 8/10 55000/55000 [==============================] - 8s 139us/sample - loss: 2.3027 - accuracy: 0.0991 - val_loss: 2.3027 - val_accuracy: 0.0986 Epoch 9/10 55000/55000 [==============================] - 8s 143us/sample - loss: 2.3027 - accuracy: 0.0961 - val_loss: 2.3028 - val_accuracy: 0.0914 Epoch 10/10 55000/55000 [==============================] - 8s 138us/sample - loss: 2.3027 - accuracy: 0.0993 - val_loss: 2.3028 - val_accuracy: 0.0976
可以用下述代码查看训练过程中的损耗和精度:
history.history
代码运行结果如下:
{'loss': [3032409856428.102,
2.302662184316462,
2.3026436624353583,
2.3026383281360974,
2.3026348412600433,
2.302653038822521,
2.3026530591097747,
2.3026501728404654,
2.3026565206701104,
2.3026550307187166],
'accuracy': [0.10018182,
0.09934545,
0.09990909,
0.0986,
0.0994,
0.09936364,
0.09910909,
0.09910909,
0.09612727,
0.09934545],
'val_loss': [2.3027801795959473,
2.302774501800537,
2.3028094802856445,
2.3028686981201174,
2.302722678375244,
2.302815665435791,
2.3028056652069093,
2.3027444290161134,
2.302812654876709,
2.3027816261291503],
'val_accuracy': [0.0914,
0.0914,
0.0986,
0.0976,
0.0976,
0.098,
0.1,
0.0986,
0.0914,
0.0976]}
五、打印训练过程曲线图
编写一段代码以实现训练过程可视化
#变化过程可视化 def plot_learning_curves(history): pd.DataFrame(history.history).plot(figsize=(8,5)) plt.grid(True) #打印网格 plt.gca().set_ylim(0,1) plt.show() plot_learning_curves(history)
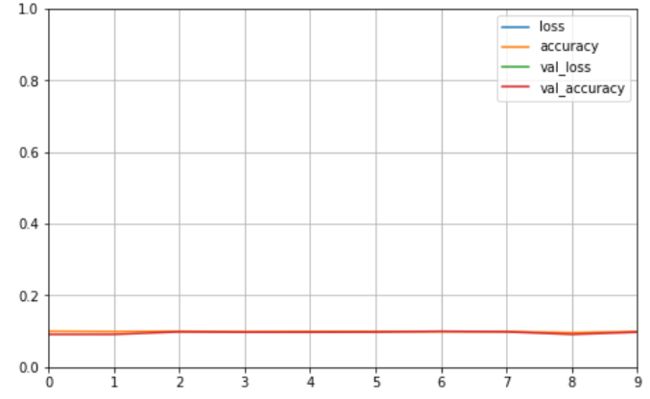
代码运行结果如下:
可以看到因为模型的的适用度和未归一化等原因,使得我们的训练效果并不是很好。