PAT甲级真题 1072 Gas Station (30分) C++实现（Dijkstra算法，测试点4四舍五入的坑）

题目

A gas station has to be built at such a location that the minimum distance between the station and any of the residential housing is as far away as possible. However it must guarantee that all the houses are in its service range.

Now given the map of the city and several candidate locations for the gas station, you are supposed to give the best recommendation. If there are more than one solution, output the one with the smallest average distance to all the houses. If such a solution is still not unique, output the one with the smallest index number.

Input Specification:
Each input file contains one test case. For each case, the first line contains 4 positive integers: N (≤1000), the total number of houses; M (≤10), the total number of the candidate locations for the gas stations; K (≤10000​​ ), the number of roads connecting the houses and the gas stations; and Ds​, the maximum service range of the gas station. It is hence assumed that all the houses are numbered from 1 to N, and all the candidate locations are numbered from G1 to GM.

Then K lines follow, each describes a road in the format

P1 P2 Dist

where P1 and P2 are the two ends of a road which can be either house numbers or gas station numbers, and Dist is the integer length of the road.

Output Specification:
For each test case, print in the first line the index number of the best location. In the next line, print the minimum and the average distances between the solution and all the houses. The numbers in a line must be separated by a space and be accurate up to 1 decimal place. If the solution does not exist, simply output No Solution.

Sample Input 1:
4 3 11 5
1 2 2
1 4 2
1 G1 4
1 G2 3
2 3 2
2 G2 1
3 4 2
3 G3 2
4 G1 3
G2 G1 1
G3 G2 2

Sample Output 1:
G1
2.0 3.3

Sample Input 2:
2 1 2 10
1 G1 9
2 G1 20

Sample Output 2:
No Solution

思路

首先处理输入中加油站的编号“G1~G10”，将其统一编号到房子之后，比如G1视为n+1。

一开始用Floyd算法求多源最短路径，果断超时了。

改用Dijkstra算法，以每个加油站为源点求单源最短路径，由于m最大值为10，最多只需求10次，解决了超时问题。

对于dist[Gi]，检查其与所有房子之间最小距离dist[Gi][i]，若其中有超过Ds的，则放弃该选择；若所有距离均在Ds内，则记录其中的最小值minGi 和平均距离 aveGi。

从所有minGi中找最大的；若有并列，再顺序找出其中aveGi最小的第一个即为所求。

坑点

1. 一开始测试点4出现运行时错误，原因是将节点编号当做了最多2位，其实它们最大能取到1000 G10 这样的，需要将除了’G’以外的所有字符串转换为数字。

2. 测试点4一直答案错误。一开始输出最后结果时为了四舍五入，将平均值加上了0.05后再用"%.1f"打印；看了网上许多代码发现并没有采用+0.05的方式，而是只有“%.1f”。查了资料发现%.1f会自动执行四舍五入的操作，但经过测试，值时3.25时打印出的是3.2，3.26时打印出3.3，值为3.251时也打印出3.3。当结果正好是X.X5时，%.1f的四舍五入结果是不对的。

去掉+0.05后，输入测试用例1，结果如下（调试环境：Mac XCode）：

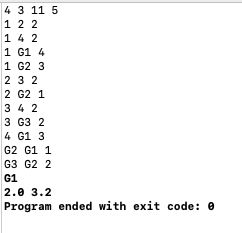
而题目中给的却是：
G1
2.0 3.3

然而这时却能AC了，测试点4不再报错……

有点神奇。如有知道问题原因的请不吝赐教。

代码

#include 
#include 
#include 
using namespace std;

struct Solution{  //可行解
    int index;
    float minDist;
    float average;
};
int main(){
    int n, m, k, ds;
    scanf("%d %d %d %d", &n, &m, &k, &ds);
    //建立邻接矩阵
    vector<vector<int> > E(n+m+1, vector<int>(n+m+1, INT_MAX));
    for (int i=0; i<k; i++){
        char a[5], b[5];  //最多要装1000，字符串大小应>=4
        int u, v, d;
        scanf("%s %s %d", a, b, &d);
        u = a[0]=='G' ? n+atoi(&a[1]) : atoi(a);
        v = b[0]=='G' ? n+atoi(&b[1]) : atoi(b);
        E[u][v] = E[v][u] = d;
    }
    //Dijkstra算法求最短路径
    vector<vector<int> > dist(m+1, vector<int>(n+m+1, INT_MAX));
    for (int i=1; i<=m; i++){
        vector<bool> visited(n+m+1);
        dist[i][n+i] = 0;
        for (int l=1; l<=m+n; l++){
            int minDist = INT_MAX;
            int minI = -1;
            for (int j=1; j<=n+m; j++){
                if (!visited[j] && dist[i][j]<minDist){
                    minDist = dist[i][j];
                    minI = j;
                }
            }
            if (minI == -1){
                break;
            }
            visited[minI] = true;
            for (int j=1; j<=n+m; j++){
                if (!visited[j] && minDist!=INT_MAX && E[minI][j]!=INT_MAX && minDist+E[minI][j]<dist[i][j]){
                    dist[i][j] = minDist + E[minI][j];
                }
            }
        }
    }

    //记录所有可行解
    vector<Solution> S;
    for (int i=1; i<=m; i++){
        float minDist = INT_MAX;
        float sum = 0.0;
        for (int j=1; j<=n; j++){
            if (dist[i][j] > ds){
                minDist = 0;
                break;
            }
            if (dist[i][j] < minDist) {
                minDist = dist[i][j];
            }
            sum += dist[i][j];
        }
        if (minDist > 0){
            S.push_back({i, minDist, sum/n});
        }
    }

    if (S.size() == 0){
        printf("No Solution\n");
    }
    else{
        //找出其中最小距离最远，平均距离最小的第一个
        Solution bestS = S[0];
        for (int i=1; i<S.size(); i++){
            if (S[i].minDist>bestS.minDist || (S[i].minDist==bestS.minDist && S[i].average<bestS.average)){
                bestS = S[i];
            }
        }
        printf("G%d\n%.1f %.1f\n", bestS.index, bestS.minDist, bestS.average);  //平均距离四舍五入
    }
    return 0;
}