视觉惯性SLAM：VINS-Mono

这篇博客

 最近看了VINS-Mono，所以就写篇关于系统各部分内容的总结，方便自己之后进行论文的回顾，也希望大家能从中有所收获。一些我认为比较重要的地方和自己的理解都用了颜色标注。好的，话不多说，直接莽。

一些符号说明

1、$(.{)}^w$：变量表示在世界坐标系下；
2、$(.{)}^b$：变量表示在$IMU$坐标系(Body坐标系)下；
3、$(.{)}^c$：变量表示在相机坐标系下；
4、$R、q$：旋转矩阵及其对应的四元数(在紧耦合的状态变量中使用)；
5、$q_b^w,p_b^w$：从$IMU$坐标系到世界坐标系的旋转和平移变换；
6、$⨂$：表示四元数之间的乘法；
7、$b_k,c_k$：第$k$帧对应的$IMU$和相机坐标系；
8、$g^w=[0,0,G{]}^T$：世界坐标系下的重力向量；
9、$\widehat{(.)}$：表示带有噪声的测量值或一个定值估计；
10、$b_w,b_a$：表示陀螺仪和加速度偏差。

IV 测量数据的预处理

 这部分介绍如何处理视觉和IMU的测量数据。大致内容为：跟踪每一帧，在新帧上提取一定数量特征点；预积分IMU数据。

A.视觉处理前端

 对于新获得的当前帧：
1、用$KLT$稀疏光流法跟踪已有特征点(上一帧中的)；
2、若跟踪到的特征点较少，则在当前帧中提取新的特征点，以保证至少有100-300个特征点（提取的特征点应满足均匀分布）；
3、用跟踪上的特征点求解前后帧的$F$单应矩阵，并用RANSAC法进行外点剔除；
4、将剩余内点反投影到当前帧的归一化平面上
 此外，这个部分还需要判断是否产生新的关键帧。判断条件是：
$\bullet$ 跟踪到的特征点的平均视差大于一定阈值；
$\bullet$ 跟踪到的特征点数量小于一定阈值。

B.IMU预积分

1)IMU的噪声和偏差：
 IMU 元件获得的原始测量值(角速度$\hat{w}$和加速度$\hat{a}$)会受到重力、偏差和噪声的影响：

这些测量值是在$t$时刻的IMU坐标系中表示 。式中$(.{)}_t$表示真实值，$n$表示白噪声。而某一时刻的加速度$b_{a_t}$和陀螺仪偏差$b_{w_t}$被建模为随机行走(它们的导数为高斯白噪声)。

2)预积分：
 先设定一个偏差的估计值，将$b_k$和$b_{k+1}$这前后两帧的 IMU 数据进行预积分。积分后的结果在$b_k$的坐标系中表示：


 可以看出，式3 中的每一项都能直接通过 IMU 的测量数据来求解，它们表示的是前后两帧之间的相对变换关系。

3)偏差修正：
 如果估计的偏差$b_{a_k}$、$b_{w_k}$发生了微小的变化，就要相应的调整预积分的结果(根据它们对$b_{a_k}$、$b_{w_k}$的雅可比矩阵)：

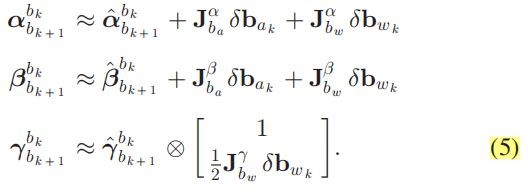
 如果偏差变化太大，则需要用新的值重新进行预积分。

V. 初始化

 通过视觉数据和IMU数据构建约束关系，以获得一些必要变量的初值。

A.Vision-Only SfM in Sliding Window

 先只使用视觉来获得一系列相机位姿和地图点坐标(未知尺度)，构建最初的滑动窗口。为控制复杂程度，只在窗口中保留一定数量的帧。
具体的步骤如下：
1、构建含有一定数量帧的滑动窗口，此时所有帧的位姿都未知；
2、获得新的帧，为其在窗口内寻找一个匹配帧(要求：匹配的特征个数多于30，同时平均视差大于20个像素单位)；
3、使用五点法恢复两帧之间的R和sp(带尺度的平移);
4、随意设一个尺度$s_{{}^{\prime }}$，对所有被两帧观测到的特征进行三角化，构建初始地图点；
5、用这些地图点估计出窗口中其他帧的位姿(使用PnP法)；
6、用BA优化各帧的位姿(优化重投影误差)。

 因为还没有关于世界坐标系的任何信息，所以将窗口内第一帧作为第一参考帧$(.{)}^{c_0}$，其余帧的位姿和地图点的坐标都用第一参考帧为基准来表示，分别记为$(.{)}_{c_k}^{c_0}，(.{)}^{c_0}$。
 根据标定好的相机到 IMU 元件的变换关系，可以将相机坐标系转换到IMU坐标系，但是 $s$ 是未知的:

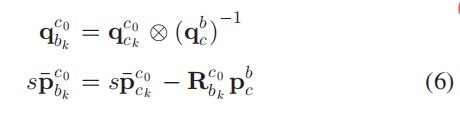
B.Visual-Inertial Alignment

 原理：将 A部分估计的位姿和IMU数据的预积分结合起来，估计出尺度、偏差等变量。（具体求解方法和 VI ORB-SLAM 存在一些不同，最大的不同在于这里使用四元数表示旋转）

1）陀螺仪偏差$b_w$估计:
 对于滑动窗口内相邻两帧有用视觉估计出的位姿$q_{b_k}^{c_0},q_{b_{k+1}}^{c_0}$，以及IMU预积分的结果${\hat{\tau }}_{k+1}^k$。所以可通过最小化下面公式的误差来获得$b_w$：

式中$B$表示窗口内所有帧。在获得$b_w$新的估计值后，重新计算一次IMU预积分。

2）速度$v$、重力向量$g^{c_0}$和尺度估计$s$：
 这一阶段估计的所有状态变量如下：

 对于滑动窗口内前后两帧$b_k,b_{k+1}$有下面的公式(这里也忽视了先加速度偏差，和VIORB一样)：

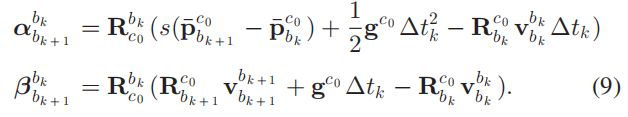
然后将式(9)和式(6)混合，可以获得下面的线性方程组：

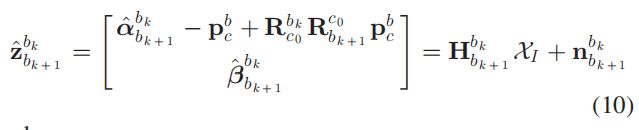
其中${\hat{z}}_{k+1}^k$是由 IMU 测量数据计算得出（带噪声），而$H_{b_{k+1}}^{b_k}$由视觉的计算结果组成：

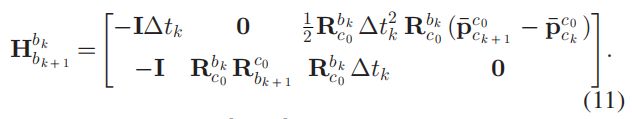
最后通过优化下面的误差获得各帧的速度，重力向量（在第一参考帧坐标系$(.{)}^{c_0}$下）和尺度:

3）优化重力向量：
 由于重力向量$g^{c_0}$的大小是已知的G，所以可以想象重力向量在一个半径为G的圆上，如图4：

此时重力向量就只有2个自由度，可在图中的重力向量的切平面上用两个正交的变量去扰动它(改变其方向)：$b1、b2$。扰动的公式为：$G(\bar{\hat{g}}+\delta g),\delta g=w_1{b}_1+w_2{b}_2$。其中G是重力的大小（用这个可能更好理解一点），$\bar{\hat{g}}$是重力的单位方向向量，$b_1、b_2$是切平面上的两个正交基；$w_1、w_2$是两个扰动方向的大小。最后$G(\bar{\hat{g}}+\delta g)$替换掉式子(9)中的$g$，将2自由度的 $\delta g$ 和其他变量一起求解（包括速度$v$、尺度$s$、加速度偏差$b_a$）。
个人理解：所有变量的求解思路和VI ORB-SLAM的思路是相似的，但更新重力向量的方式有所不同

4）完成初始化：
 使用最终求出的重力向量与真实世界的重力向量$[0,0,-1{]}^T$，求出$q_{c_0}^w$，即第一参考帧与世界坐标系之间的变换关系。然后将地图点都转到世界坐标系中，轨迹也用求出的尺度进行修正。

VI.TIGHTLY COUPLED MONOCULAR VIO

 在滑动窗口内求解每个视觉+惯性的紧耦合状态变量，如图5所示：

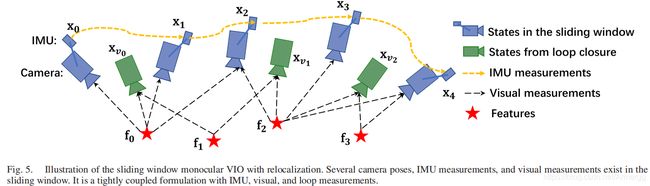
A.公式介绍

 紧耦合后的状态变量如下：

$x_k$是第$k$个状态变量，包含位姿、速度和偏差。${\lambda }_l$是第 $l$ 个地图点在其第一观测帧中的逆深度。此时待优化的误差函数为：

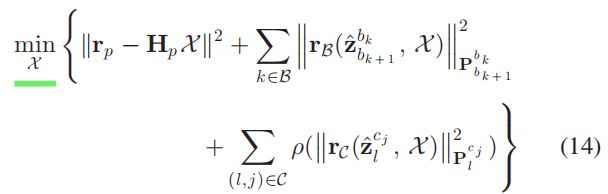
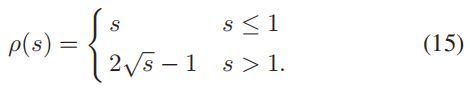
式中第一项是先验误差，第二项是 IMU 误差，第三项是重投影误差，式(15) 表示鲁棒核函数。

B.IMU误差

 滑动窗口内相邻两帧间的IMU误差为：

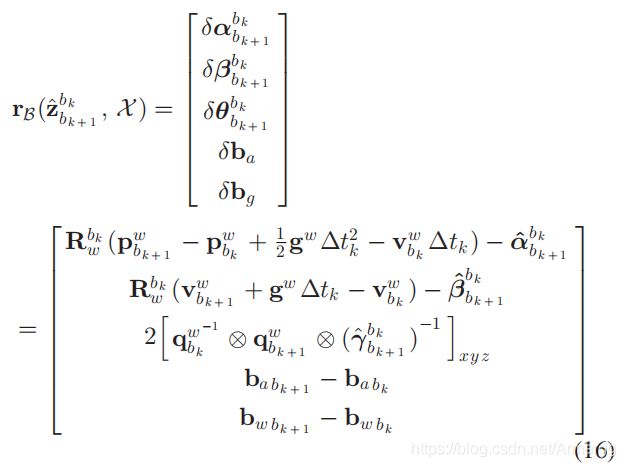
式中[.]XYZ表示提取出四元数Q中的向量部分来表示误差状态。

个人理解：每一个误差项=当前估计的状态变量求出的相对变换 — IMU预积分求出的相对变换。

C.视觉误差

 在归一化平面上计算视觉误差。以在第 $i$ 帧上观测到的第 $l$ 个地图点为例，他在第 $j$ 帧上的视觉误差为：
式中$\pi$是相机投影函数；$u，v$是像素坐标。
 由于上述视觉误差的自由度为2，所及将误差向量投影到切平面上，并用两个正交方向上的扰动来优化误差，如图6所示：

个人理解：这里的2自由度是因为重投影误差是在归一化平面上的，有一维坐标一直为1

D.边缘化

 用这个方法控制滑动窗口内KF和地图点的数量，并把边缘化的帧作为一个先验信息。边缘化的两种情况如图7所示：

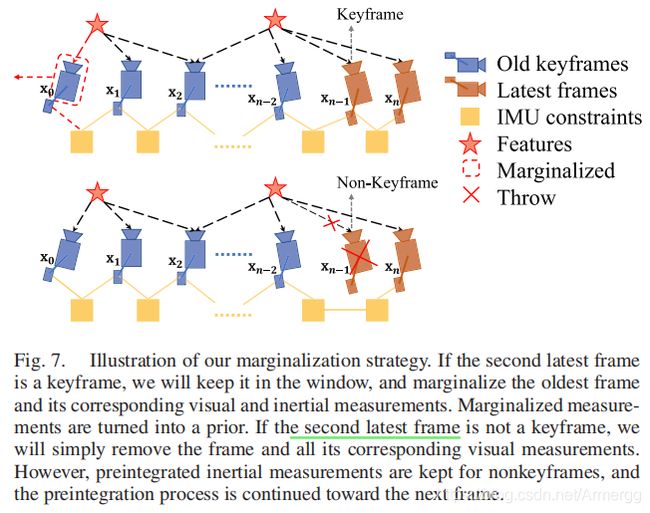
 图中棕色图形表示两个最新的帧，此时边缘化的操作有两种：
1、若图中n-1帧是KF，则将其放入窗口中，并把窗口中最老的KF丢掉。（但保留它的IMU信息作为先验）
2、若n-1帧不是KF，则只保留它的IMU预积分结果，也作为一个先验信息。（帮助计算KF与下一帧之间的IMU预积分）
（对第一种情况的先验信息不是很理解）

E.位姿优化

 为了降低计算量，只进行运动上的位姿优化，如图8所示：

 如图所示，不优化窗口内的所有$KF$，只优化最近一定数量的$KF$和当前帧。优化时使用的误差式子和式（14）一样，即 IMU 误差、视觉误差和先验误差。

F.以IMU采集的速率估计位姿值

 系统的处理速率受帧速率影响，但可以结合最新帧的估计值，使用之后一系列(在下一帧到来前的）的IMU数据来获得和IMU采集速率一样的位姿估计。这个高速率的估计值可用于闭环的状态反馈。(最后一句话不是很理解，期待各位博友指点迷津)

VII 重定位（和VI ORB不同）

 作用：消除累积误差（漂移）

A.闭环检测

 使用DBOW2词袋中的单词来描述每一帧，再通过这个描述完成闭环检测。(这一部分可参考《视觉SLAM十四讲》P303)

B.特征找回

目的：确定闭环对应的两个$KFs$之间的特征匹配和变换关系。
 当检测到闭环后，窗口（一般是当前最新的$KF$）与匹配的闭环帧（记为$K{F}_v$）（来自系统保存$KFs$的数据库中）的关系就能被建立起来（通过特征匹配）。为了降低误匹配，使用下面两个几何的方法来去除外点：
1）2d-2d：通过RANSAC求出$K{F}_v$和当前$KF$之间的单应矩阵$F$。
2）3d-2d：将滑动窗口内已有地图点，和其在$K{F}_v$上匹配的观测点进行基于RANSAC法的PnP问题求解。
 如此就能求出$v$和当前$KF$之间的变换关系，并剔除了外点。

C.紧耦合的重定位

目的：发现闭环后，将当前滑动窗口与以往帧进行位姿对齐。
 窗口内每产生一个新的$KF$就为其在数据库中查询是否存在匹配的闭环KF。在找到匹配的闭环$KF$后（记为$K{F}_v$），将它作为一个闭环约束，构建一个新的误差函数：

式中$K{F}_v$提供的约束就是滑动窗口内地图点在$K{F}_v$上的重投影误差，它可以帮助修正窗口的所有地图点坐标和$KFs$的位姿。图9展示了整个闭环检测和重定位的过程：

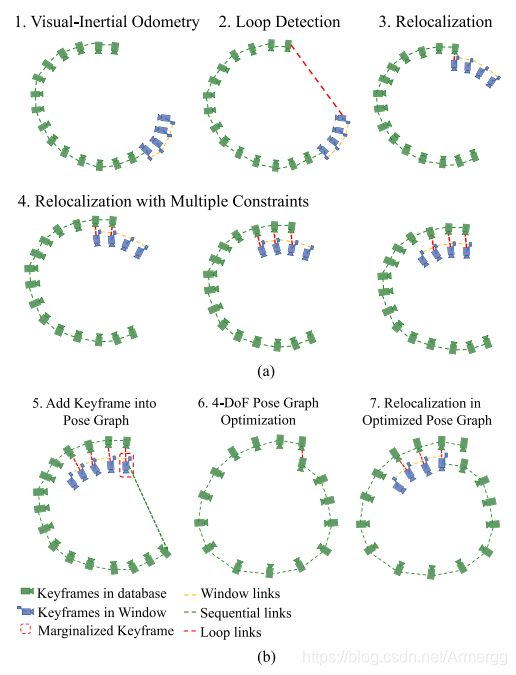
 从图中可以看出，前三步为：正常跟踪、发现闭环、重定位滑动窗口。在这之后，窗口内还有不断产生新的$KF$，新来的KF也可能找到对应的闭环帧，所以闭环约束就会增加，这就形成了多视图约束。
个人理解 ：在第一个发生闭环的KF即将被边缘化时，进行一次全局BA，把整体轨迹整合进行修正。

VIII全局优化和地图复用

A.四个存在漂移问题的变量

 受益于重力向量的惯性测量，系统可以估计$(.{)}^{b_i}$与$(.{)}^w$在roll、pitch上的绝对旋转（x，y轴旋转，z轴的旋转不会影响重力向量的方向），如图11所示。此时只会在$x，y，z，yaw$四个变量上产生累积误差。所以全局位姿图优化只用优化这四个变量。

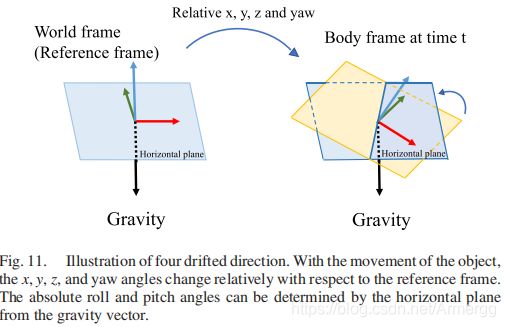
B.向位姿图中加KF

 视觉-惯性里程计处理后的KF会加到位姿图中。它 会被当作一个顶点，并通过两类边和其他顶点产生联系：
1） 连续边：某个$KF$与之前的$KFs$之间的相对变换关系。只管那四个变量：

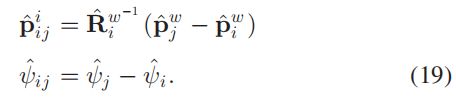
2） 闭环边：只有形成闭环的$KFs$之间才有，表示它们之间的相对变换，公式和式(19)一样。
 整个位姿图的样子就如下图所示：

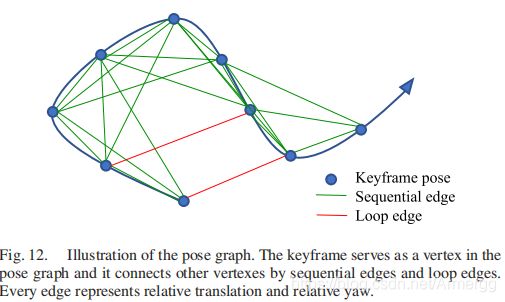
C. 4自由度的位姿图优化

 定义$i、j$两个KF之间的边的误差为：

其中$\hat{\theta },\hat{\varphi }$是固定的。整个位姿图中所有边产生的总误差公式为：

式中$S$ 为所有连续边，$L$为闭环边。$\rho$ 是鲁棒核函数。
 位姿图优化和重定位在两个异步的线程中同时进行，目的是：
1、可让数据库中优化后的位姿图立马能用于新的重定位操作中（异步不用互相等待）；
2、

D.位姿图合并

 通过地图间的闭环关系，将当前构建的位姿图与已有的位姿图合并。找到闭环关系后，直接使用全局BA即可。过程如图13所示：

E.位姿图保存

 数据的保存内容：所有顶点和边；关键帧（顶点）的状态变量。
举个例子：

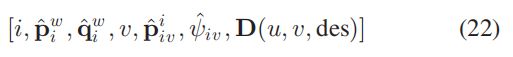
其中 $i$ 表示帧的编号，${\hat{p}}_i^w$、${\hat{q}}_i^w$是这一帧的平移和旋转变换(从当前帧到世界坐标系)。$v$是与这个帧形成闭环的匹配帧的编号，${\hat{p}}_{iv}^i$和${\hat{\psi }}_{iv}$是他们之间的相对位移和 $yaw$ 方向的旋转角度（由重定位获得）。$D(u,v,des)$是这一帧中的特征点坐标和它对应的描述子。

F.加载位姿图

 怎么保存的就怎么加载。

结尾

 一口气看完两篇视觉惯性SLAM，感觉也大致懂了这类SLAM的工作原理。还是要抓紧看代码，毕竟编程能力十分重要（太忙了）。最后希望这篇博客能帮助到大家，其中存在的不足也希望大家能够指出，十分感谢！

参考资料：
1、VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator
2、《视觉SLAM十四讲》