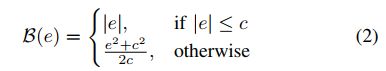稀疏到稠密：从稀疏深度样本+单一图像的深度预测(Sparse-to-Dense: Depth Prediction from Sparse Depth Samples and..)

目录

论文出处

摘要

I 介绍

II 相关工作

A 基于RGB的深度预测

B. 从稀疏样本进行深度重建

C. 传感器融合

III 方法

C. CNN架构

B.  深度采样

C. 数据扩充

D.损失函数

IV. 实验内容

A. NYU-Depth-v2数据集

B. KITTI里程表数据集

C. 误差指标

V. 实验结果

A.网路结构评估

B.与最新技术的比较

1）NYU-Depth-v2数据集

2）KITTI数据集

C.深度样本数

D.应用：视觉里程计特征的密集地图

E.应用：LiDAR超分辨率

VI. 结论

参考

---

论文出处

• 题目： Sparse-to-Dense: Depth Prediction from Sparse Depth Samples and a Single Image
• 出处： Mal F, Karaman S. Sparse-to-Dense: Depth Prediction from Sparse Depth Samples and a Single Image[C]. international conference on robotics and automation, 2018: 1-8.
• 代码地址： https://github.com/fangchangma/sparse-to-dense
• 视频展示：https://www.youtube.com/watch?v=vNIIT_M7x7Y

摘要

        我们关注的是从一组稀疏的深度测量和一个单一的RGB的图像，作稠密深度预测问题。由于深度估计单目图像单独是固有的模棱两可和不可靠，为达到一个更高的水平鲁棒性和准确性，我们引入了额外的稀疏深度样本，这些样本要么是在低分辨率的深度传感器获得或通过SLAM算法获得。我们提出使用一个单一深度的回归网络（a single deep regression network）直接从RGB-D原始学习数据，并探讨样本深度数对数据的影响预测精度。

       我们的实验表明，与只使用RGB图像，随机添加100个空间深度样本降低了预测的均方根误差对NYU-Depth-v2室内数据集增加50%。它在KITTI数据集上，也提高了可靠预测的百分比（从59%上升到92%）。我们提出了两种应用程序算法:在SLAM插件模块中进行稀疏地图到密集地图的转换，和LiDARs的超分辨率。软件和视频演示都是公开的。

I 介绍

       深度感应和估计在以下方面至关重要广泛的工程应用，例如机器人技术，自动驾驶，增强现实（AR）和3D映射。 但是，现有的深度传感器（包括LiDAR）基于结构光的深度传感器和立体声相机，全部有自己的局限性。 例如，范围最广的3D LiDAR成本过高（每项成本高达75,000美元），但仅提供远距离稀疏的测量对象。 基于结构光的深度传感器（例如Kinect）是阳光敏感且耗电，范围短距离。 最后，立体相机需要较大的基线，仔细校准以实现精确的三角剖分要求大量的计算，通常在无特征时失败地区。 由于这些限制，一直存在对使用单个摄像头进行深度估算非常感兴趣，它体积小，成本低，节能，在消费电子产品中无所不在。

       虽然基于RGB的深度预测的研究，包括深度学习方法的最新改进，已经有十多年研究历史了，但这种方法的准确性和可靠性但仍然离实践还很远。 例如，基于RGB的最新深度预测方法[1-3]产生平均误差（在室内超过50cm的均方根误差）场景（例如，在NYU-Depth-v2数据集[4]上）。这样的方法在室外Make3D和KITTI数据集的平均误差[5，6]上表现更差，误差至少4米。

       为了解决基于RGB的深度估计的潜在基本限制，我们考虑利用稀疏深度测量以及RGB数据，以进行重建完整分辨率的深度。 稀疏深度测量是在许多应用中都可以轻松获得。 例如，低分辨率深度传感器（例如，低成本LiDAR）可提供这样的测量。 稀疏深度测量也可以根据SLAM的输出和视觉惯性里程计算法获得。在这项工作中，我们证明了除了RGB图像以外，使用稀疏深度测量作为系统输入的一部分的有效性。 我们使用单个卷积神经网络来学习用于深度图像预测的深度回归模型。 我们的实验结果表明，添加少至100个深度样本在NYU-Depth-v2数据集上将均方根误差降低了50％以上，而在更具挑战性的数据集上，可靠预测的百分比从59％提高到了92％ KITTI户外数据集。总的来说，我们的结果表明，添加几个稀疏深度样本可以大大提高深度重建性能。 我们的定量结果可能有助于为未来的机器人车辆和消费类设备开发传感器。

        本文的主要贡献是一种深度回归模型，该模型将稀疏的深度样本集和RGB图像作为输入，并预测了全分辨率深度图像。 我们方法的预测准确性大大优于现有方法，包括基于RGB和基于融合的技术。 此外，我们在实验中证明我们的方法可以用作插件模块来稀疏视觉里程表/ SLAM算法，以创建准确的密集点云。 此外，我们证明了我们的方法还可以用于3D LiDAR中以创建更密集的测量。

II 相关工作

A 基于RGB的深度预测

早期使用RGB图像进行深度估计的工作，通常依赖于手工特征（hand-craftedfeatures）和概率图形模型（probabilistic graphical models）。 例如，Saxena等[8]估计不同图像块的绝对比例，并使用马尔可夫随机场模型推断深度图像。 非参数方法[9-12]则通过将图像的深度与从数据库中检索到的相似光度内容相结合，来估计查询图像的深度。

最近，深度学习已成功应用于深度估计问题。

• Eigen等[13]提出了一个两层卷积神经网络（CNN），其中一个预测全局粗尺度，另一个预测局部细节。
• Eigen和Fergus [2]进一步将其他辅助预测任务合并到同一体系结构中。刘等[1]结合了一个深的CNN和一个连续的条件随机场，并在视觉上获得了更清晰的过渡和局部细节。
• Laina等[3]基于ResNet [14]开发了一个深度残差网络，并且比[1，2]获得了更高的精度。
• 半监督[15]和无监督学习[16-18]的设置也已用于视差图像预测。例如，Godard等[18]将视差估计公式化为图像重建问题，其中训练了神经网络使左图像变形以匹配右图像。

B. 从稀疏样本进行深度重建

另一相关工作是从稀疏样本进行深度重建。该领域中许多方法的共同点是对深度信号使用稀疏表示。例如，

• Hawe等[19]假设视差图在小波基础上是稀疏的，并使用共轭次梯度法重建了密集的视差图像。
• 刘等[20]结合了小波和轮廓波字典（wavelet and contourlet dictionaries）进行更精确的重建。
• 我们先前在稀疏深度感测中的工作[21，22]利用了深度图像二阶导数背后的稀疏性，并且在重建精度和速度方面均优于[1,19]。

C. 传感器融合

       各种各样的技术试图通过融合来自不同传感器模式的其他信息来改善深度预测。例如，

• Mancini等[23]提出了一个CNN，它同时接收RGB图像和光流图像作为预测距离的输入。
• 廖等[24]研究了安装在移动地面机器人上的2D激光扫描仪的使用，以提供额外的参考深度信号作为输入，并且比单独使用RGB图像获得更高的精度。与廖等人的方法相比，[24]这项工作不假设传感器的方向或位置，也不假设输入深度样本在像素空间中的空间分布。
• Cadena等[25]开发了一种多模式自动编码器，可以从三种输入模式中学习，包括RGB，深度和语义标签。在他们的实验中，Cadena等人[25]在提取的FAST拐角特征上使用稀疏深度作为系统输入的一部分，以产生低分辨率的深度预测。准确性可与单独使用RGB相媲美。相比之下，我们的方法预测了全分辨率深度图像，学习了更好的RGB和稀疏深度的交叉模态表示，并且获得了明显更高的精度。

III 方法

在本节中，我们描述了卷积神经网络的体系结构。我们还将讨论深度采样策略，数据增强技术以及用于训练的损失函数。

C. CNN架构

我们在实验中发现，许多瓶颈（bottleneck）架构（带有编码器和解码器）都可以带来良好的性能。为了进行基准测试，我们选择基于[3]的最终结构，因为它在基于RGB的深度预测中达到了最先进的精度。网络为我们的问题提供了不同形式，大小和尺寸的输入数据。对于KITTI和NYU-Depth-v2，我们使用两个不同的网络。这是因为KITTI映像的大小是NYU-Depth-v2的三倍，因此相同的体系结构将需要3倍的GPU内存，超出了当前的硬件容量。最终结构如图2所示。

网络的特征提取（编码）层以蓝色突出显示，由ResNet [14]和卷积层组成。更具体地说，ResNet-18用于KITTI，ResNet-50用于NYU-Depth-v2。原始ResNet的最后一个平均合并层和线性转换层已被删除。编码结构的第二个部分，即卷积层，内核大小为3×3。
以黄色突出显示的解码层由4个上采样层和一个双线性上采样层组成。我们使用Laina等人提出的UpProj模块。 [3]作为我们的上采样层，但是具有较大内核大小的反卷积也可以达到相同的精度水平。第V-A节显示了不同上采样层的经验比较。

B.  深度采样

在本节中，我们介绍了根据真值(ground truth)创建输入稀疏深度图像的采样策略。

在训练期间，动态地从真值深度图像D*中随机采样输入的稀疏深度D。 特别是，对于任何深度样本的目标数量(targeted number of depth samples) m（在训练期间固定），我们计算伯努利概率(Bernoulli probability) p = m / n，其中n是D*中有效深度像素的总数。 然后，对于任何像素（i; j）

通过这种采样策略，每个训练样本的非零深度像素的实际数量，在期望值m左右变化。 请注意，此采样策略不同于dropout[26]，后者在训练过程中将输出按1/p比例缩放以补偿失活的神经元。 我们的抽样策略的目的是针对不同数量的输入来提高网络的健壮性，并创建更多的训练数据（即数据增强技术）。 值得探讨的是随机噪声的注入和不同的采样策略（例如特征点）将如何影响网络性能。

C. 数据扩充

我们以在线方式通过随机变换来扩充训练数据，包括

• 缩放：彩色图像按随机数s ∈[1, 1.5]，深度除以s。
• 旋转：颜色和深度都以随机度r ∈ [−5, 5]。
• 色彩抖动：彩色图像的亮度，对比度和饱和度均按ki ∈[0.6, 1.4]。
• 颜色归一化：RGB通过均值减法并除以标准差进行归一化。
• 翻转：颜色和深度都可以50％的机会水平翻转。

在缩放和旋转中都使用最近邻居插值，而不是更常见的双线性插值或双三次插值，以避免产生虚假的稀疏深度点。 我们从增强图像中获取中心裁剪，以便网络的输入大小保持一致。

D.损失函数

回归问题的损失函数的一种常见的默认选择是均方误差（L2）。 L2对训练数据中的异常值很敏感，因为它对更大的误差有更大的惩罚作用。 在我们的实验过程中，我们发现L2损失函数还会产生视觉上不希望的，过度平滑的边界，而不是尖锐的过渡。
另一个常见选择是Reversed Huber（表示为berHu）损失函数[27]，定义为

[3]使用批次相关的参数（a batch-dependent parameter）c，作为批次中所有像素上最大绝对误差的20％来计算。 直观上，当元素方向的误差降至c以下时，berHu充当平均绝对误差（L1），而当误差超过c时，berHu近似充当L2。

在我们的实验中，除了上述两个损失函数外，我们还测试了L1，发现它在基于RGB的深度预测问题上产生了稍好的结果。 经验比较显示在第V-A节中。 因此，出于简洁和性能的考虑，我们在整个白皮书中将L1用作默认选择。

IV. 实验内容

我们使用Torch [28]来实现网络。 我们的模型使用具有16GB内存的NVIDIA Tesla P100 GPU在NYU-Depth-v2和KITTI里程表数据集上进行训练。 ResNet在编码层中的权重（除了第一层中具有不同数量的输入通道）使用在ImageNet数据集上预先训练的模型来初始化[29]。 我们使用batch值为16，训练20个epochs。 学习率从0.01开始，每5个周期降低到20％。 进行e10-4(0.0001)的较小权重衰减，以进行正则化。

A. NYU-Depth-v2数据集

NYU-Depth-v2数据集[4]由RGB和深度图像组成，这些图像是使用Microsoft Kinect从464种不同室内场景中收集的。 我们使用官方的数据划分，其中249个场景用于训练，其余215个场景用于测试。 特别是，为了进行基准测试，使用带有小标签的654张图像测试数据集来评估最终性能，如先前的工作[3，13]所示。

为了进行训练，我们从训练数据集中的每个原始视频序列中对空间进行均匀采样，从而生成大约48k同步深度RGB图像对。 深度值被投影到RGB图像上，并使用官方工具箱用双边过滤器进行内画（in-painted）。 如同[3,13]，首先将原始尺寸为640×480的帧降采样为一半，然后进行中心裁剪，最终尺寸为304×228。

B. KITTI里程表数据集

在这项工作中，我们使用里程计数据集（odometry dataset），其中包括相机和LiDAR测量。 里程表数据集由22个序列(sequences) 组成。 其中一半用于训练，另一半用于评估。 我们使用来自训练序列的所有46k张图像来训练神经网络，并使用来自测试序列的3200个图像的随机子集进行最终评估。
我们将左右RGB相机都用作独立的镜头(john:这合理吗？)。 Velodyne LiDAR测量值投影到RGB图像上。 由于LiDAR不会将测量结果返回到图像的上部，因此仅使用底部的裁切（912×228）。 与NYU-Depth-v2相比，即使对于KITTI来说，ground truth 也是稀疏的，通常在208k图像像素中只有18k的投影测量值。（john: 具体数据怎么对齐未说明？ground truth直接是对齐的？）

C. 误差指标

我们使用以下指标评估每种方法：

• RMSE：均方根误差
• REL：平均绝对相对误差
• δi：相对误差在阈值内的，预测像素的百分比。 特别地，
  • 
  • 其中yi和y ^ i分别是ground truch 和 prediction，而card是集合的基数。 较高的δi表示更好的预测。

V. 实验结果

在本节中，我们介绍所有实验结果。 首先，我们在第V-A节中评估了具有不同损失函数和网络组件对预测精度的影响。 其次，我们在V-B部分的NYU-Depth-v2和KITTI数据集上将建议的方法与最新方法进行了比较。 第三，在第V-C节中，我们探讨了稀疏深度样本数量对性能的影响。 最后，在第V-D节和第V-E节中，我们演示了我们提出的算法在创建密集地图和LiDAR超分辨率方面的两个用例。

A.网路结构评估

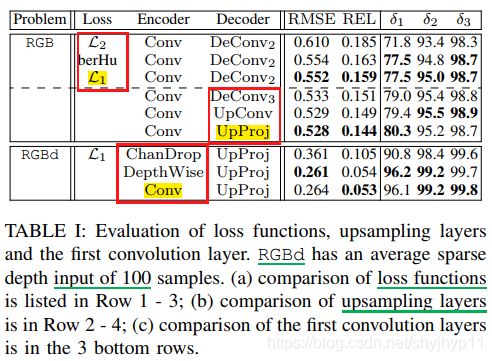
在本节中,我们对不同损耗函数和网络组件对深度预测精度的影响进行了实证研究。结果列在表I中。

1）损失函数：为了比较损失函数，我们使用相同的网络体系结构，其中上采样层是使用2×2内核（表示为DeConv2）的简单反卷积。为了比较，在表I的前三行中列出了L2，berHu和L1损失函数。如表所示，berHu和L1均明显优于L2。此外，L1比berHu产生更好的结果。因此，我们使用L1作为损失函数的默认选择。

2）上采样层：我们对不同的上采样层进行实证评估，包括对具有不同大小的内核（DeConv2和DeConv3）以及Laina等人提出的UpConv和UpProj模块进行反卷积 [3]。结果列于表I的第3至6行。

我们做了一些观测。首先，在每个指标中，使用3×3内核（即DeConv3）进行反卷积的性能优于仅使用2×2内核（即DeConv2）进行反卷积的性能。其次，由于DeConv3和UpConv都具有3×3的接受区域（a receptive field）（意味着每个输出神经元都是从9个输入神经元的邻域计算得出的），因此它们具有可比的性能。第三，UpProj模块具有更大的4×4接收区域（a receptive field），其性能优于其他模块。我们选择使用UpProj作为默认选项。

3）第一个卷积层：由于我们的RGBd输入数据来自不同的感应方式，因此它的4个输入通道（R，G，B和深度）具有非常不同的分布和支持。我们在第一个卷积层上执行简单的分析，并探索三个不同的选项。
第一种选择是规则空间卷积（Conv）。第二种选择是深度可分离卷积（表示为DepthWise），它由在每个输入通道上独立执行的空间卷积组成，然后是窗口大小为1的跨不同通道的逐点卷积。第三种选择是通道dropout（表示为ChanDrop），通过该通道，每个输入通道以一定的概率p保持原样，并以概率1-p归零。

底部的3行会比较3个选项的结果。 使用平均100个稀疏输入样本的RGBd输入来训练网络。 DepthWise和Conv产生非常相似的结果，并且两者的性能都大大优于ChanDrop层。 由于差异很小，为了比较的一致性，我们将在所有实验中使用卷积层。

B.与最新技术的比较

在本节中，我们将与现有方法进行比较。

1）NYU-Depth-v2数据集

我们与基于RGB的方法[3、13、30]以及融合方法[24]（使用安装在地面机器人上的附加2D激光扫描仪）进行了比较。 定量结果列于表II。

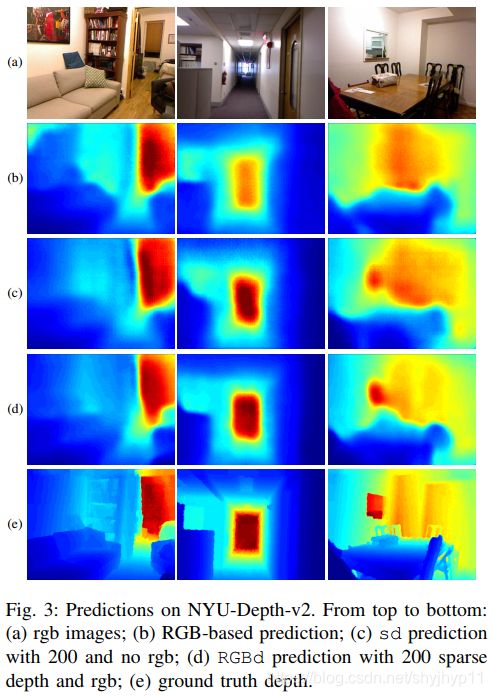
我们从第2行和第3行的第一个观察可以看出，在相同的网络体系结构下，通过用简单的L1代替[3]中提出的berHu损失函数，我们可以获得稍好一点的结果（尽管REL更高）。其次，通过比较问题组RGB（第3行）和问题组sd（例如第4行），我们得出的结论是，与20个稀疏深度样本（没有颜色信息）相比，使用样本非常少的一组已经产生了比使用RGB更好的预测。第三，通过将问题组sd和问题组RGBd逐行比较相同数量的样本，很明显，颜色信息确实有助于提高预测精度。换句话说，我们提出的方法能够从RGB图像和稀疏深度图像中学习合适的表示形式。最后，我们与[24]（下排）进行比较。我们提出的方法，即使仅使用100个样本，在225次激光测量中也优于[24]。这是因为我们的样本在空间上是均匀的，因此比线测量提供更多的信息。图3显示了我们使用不同输入进行预测的一些示例。

2）KITTI数据集

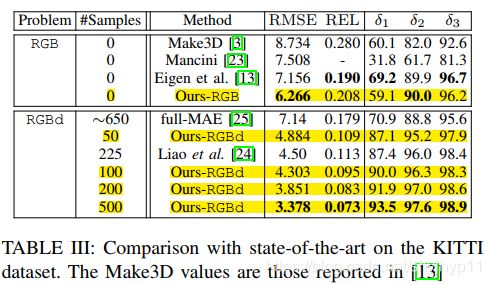
KITTI数据集对于深度预测更具挑战性，因为最大距离为100米，而NYU-Depth-v2数据集中的最大距离仅为10米。使用我们的方法可以提高性能。尽管不同方法上的训练和测试数据并不相同，但从某种意义上说，场景都是相同的，它们都来自汽车上的同一传感器设置，并且在行驶过程中收集了数据。我们在表III中报告了每项工作的值。

第一个RGB组中的结果表明，基于RGB的深度预测方法在室外场景中会失败，其像素级RMSE接近7米。 请注意，我们稀疏标记了从LiDAR投影的深度图像，而不是像[13]中那样从立体相机计算的密集视差图。 换句话说，与[13，23]相比，我们的训练数据集要小得多。

另外500个深度样本将RMSE提升至3.3米，是RGB方法的一半，并将δ1从仅59.1％提高到了93.5％。 我们的性能也优于包括[24，25]在内的其他融合技术，同时所需的样本更少。

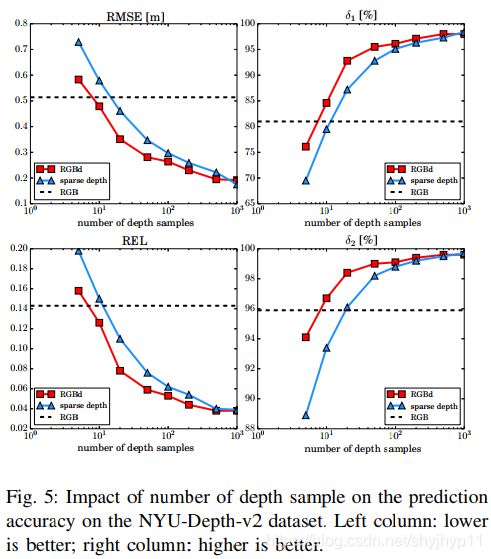
C.深度样本数

在本节中，我们探讨了预测精度与可用深度样本数量之间的关系。 我们针对每种不同的输入大小训练网络，以实现最佳性能。 我们比较了所有三种输入数据（包括RGB，sd和RGBd）的性能。 基于RGB的深度预测的性能与输入样本大小无关，因此被绘制为用于基准测试的水平线。

在图5的NYU-Depth-v2数据集上，RGBd优于RGB的深度样本超过10个，并且性能差距随着样本数量的增加而迅速增加。对于一组100个样本，RGBd的RMSE减小到25cm左右，是RGB的一半（51cm）。 REL的改善更大（从0.15减少到0.05，减少了三分之二）。一方面，RGBd方法始终优于sd，这表明学习的模型确实不仅能够从稀疏样本中提取信息，而且还可以从颜色中提取信息。另一方面，随着样本数量的增加，RGBd和sd之间的性能差距会缩小。

当样本大小增加到1000时，这两种方法的性能均相同，这仅占图像像素的不到1.5％，并且与图像大小相比仍然很小。该观察结果表明，当样本大小足够大时，从稀疏样本集中提取的信息将主导预测，在这种情况下，颜色提示几乎变得无关紧要。

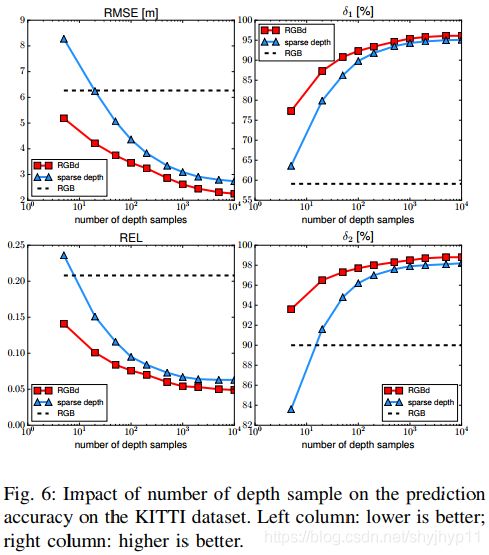
如图6所示，KITTI数据集的性能增益几乎与NYU-Depth-v2相同。通过100个样本，RGBd的RMSE从7米降低一半到3.5米。这与NYU-Depth-v2数据集的改善百分比相同。同样，REL从0.21降低到0.07，与NYU-Depth-v2的改善百分比相同。

在两个数据集上，精度都随着深度样本数量的增加而饱和。此外，即使有许多深度样本，预测也具有模糊的边界（请参见图8）。我们认为，这两种现象都可以归因于bottleneck网络体系结构中丢失了详细信息的事实。从编码器到解码器的其他跳过连接是否有助于提高性能，还有待进一步研究。

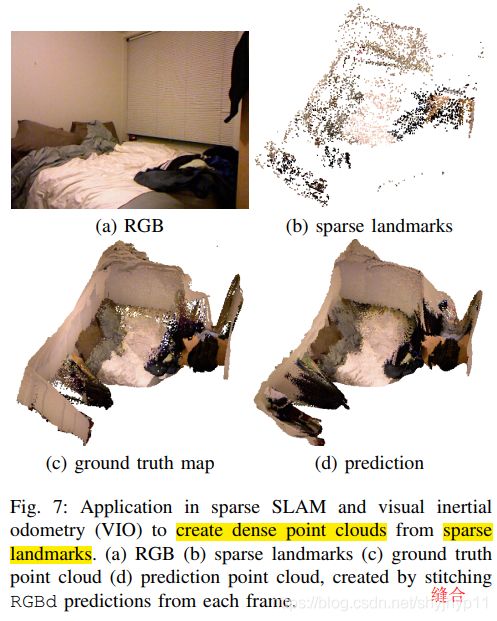
D.应用：视觉里程计特征的密集地图

在本节中，我们演示了我们提出的方法在稀疏视觉SLAM和视觉惯性里程表（VIO）中的用例。 SLAM和VIO的最佳算法通常是稀疏方法，该方法用稀疏3D地标表示环境。 尽管稀疏SLAM / VIO算法是鲁棒且高效的，但输出图以稀疏点云的形式出现，对于其他应用程序（例如运动计划）没有用。

为了证明我们提出的方法的有效性，我们使用来自NYU-Depthv2数据集中测试场景之一的数据，实现了一种简单的视觉测距（VO）算法。为简单起见，绝对尺度（absolute scale）是从第一帧的 ground truth 深度图像得出的。 VO生成的3D landmarks
被反投影到RGB图像空间上，以创建稀疏深度图像。我们将RGB和稀疏深度图像都用作预测的输入。仅保留受信任区域内的像素（我们将其定义为由输入稀疏深度样本形成的像素空间上的凸包），因为它们受到了很好的约束，因此更加可靠。然后从这些可靠的预测中重建密集点云，并使用来自VIO的轨迹估计将它们缝合在一起。
结果如图7所示。预测图与 ground truth 图非常相似，并且比VO的稀疏点云更密集。我们的预测和 ground truth 之间的主要区别在于，预测图在白墙上只有很少的点，VO不会提取或跟踪任何特征。结果，与白墙相对应的像素落在受信任区域之外，并因此被去除。

E.应用：LiDAR超分辨率

我们展示了该方法的另一个演示：在LiDAR测量的超分辨率表示。 3D LiDAR具有较低的垂直角分辨率，因此会生成垂直稀疏的点云。我们将稀疏深度图像和RGB图像中的所有测量值用作网络的输入。平均REL为4.9％，而仅使用RGB时为20.8％。图8中显示了一个示例。与原始扫描相比，汽车在预测中的识别度更高。

VI. 结论

我们引入了一种新的深度预测方法，可以从RGB图像和稀疏深度图像中预测密集的深度图像，非常适合传感器融合和稀疏SLAM。我们证明了这种方法仅使用RGB图像和其他现有的RGB-D融合技术就大大优于深度预测。该方法可用作稀疏SLAM和视觉惯性里程计算法以及LiDAR测量超分辨率中的插件模块。我们相信，这种新方法为RGBD学习和更一般的3D感知问题的研究开辟了一条重要途径，而稀疏深度样本可能会从中受益匪浅。

待研究：

1. Laina等人提出的UpProj模块 ？看代码+论文[3]

参考

[3] I. Laina, C. Rupprecht et al., “Deeper depth prediction with fully convolutional residual networks,” in 3D Vision (3DV), 2016 Fourth International Conference on. IEEE, 2016, pp. 239–248.

[13] D. Eigen, C. Puhrsch, and R. Fergus, “Depth map prediction from a single image using a multi-scale deep network,” in Advances in neural information processing systems, 2014, pp. 2366–2374