pytorch: 计算ConvTranspose1d输出特征大小

问题：如何经过convTransposed1d输出指定大小的特征？

import torch
from torch import nn
import torch.nn.functional as F


conv1 = nn.Conv1d(1, 2, 3, padding=1)
conv2 = nn.Conv1d(in_channels=2, out_channels=4, kernel_size=3, padding=1)
#转置卷积
dconv1 = nn.ConvTranspose1d(4, 1, kernel_size=3, stride=2, padding=1, output_padding=1)

x = torch.randn(16, 1, 8)
print(x.size())

x1 = conv1(x)
x2 = conv2(x1)
print(x2.size())

x3 = dconv1(x2)
print(x3.size())

'''
torch.Size([16, 1, 8])
torch.Size([16, 4, 8]) #conv2输出特征图大小
torch.Size([16, 1, 16]) #转置卷积输出特征图大小
'''

计算转置卷积输出特征大小公式
输入：$(N,C_{in},L_{in})$
输出：$(N,C_{out},L_{out})$

计算$L_{out}$大小：
$L_{out}=(L_{in}-1)\times stride-2\times padding+dilation\times (kernelsize-1)+outputpadding+1$

dilation默认为1， 上式简写为：
$L_{out}=(L_{in}-1)\times stride-2\times padding+kernelsize+outputpadding$
kernel_size固定，由stride, padding, outputpadding共同决定输出特征大小。

问题：输出特定的$L_{out}$大小
假如$L_{in}=8,L_{out}=23,kernelsize=3,outputpadding=1$，根据上式可以求得：$stride=3,padding=1$

#转置卷积
dconv1 = nn.ConvTranspose1d(1, 1, kernel_size=3, stride=3, padding=1, output_padding=1)

x = torch.randn(16, 1, 8)
print(x.size()) #torch.Size([16, 1, 23])


x3 = dconv1(x)
print(x3.size()) #torch.Size([16, 1, 23])

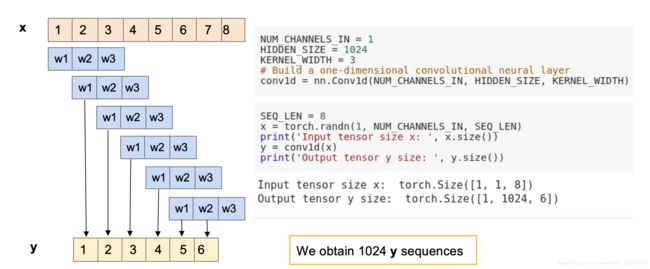
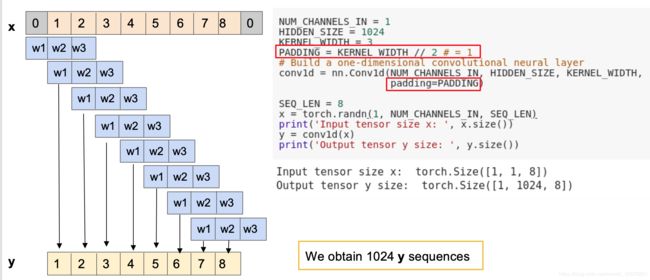
下面两图为演示conv1d，在padding和不padding下的输出特征图大小

不带padding

带padding