「图形学/渲染管线/图元装配」透视投影矩阵的推导和原理解释
文章目录
- 前言
- 前置知识
- 视见体和标准设备坐标系
- 透视投影
- 原理
- 目的/结果
- 透视投影矩阵的推导
- 1. 计算视锥体的点投影到近平面的x、y坐标
- 2. 规范化近投影面的x、y坐标
- 3. 透视除法消除非线性变换
- 4. 计算视锥体的点投影后的深度(z)
- 5. 得到透视投影矩阵
- 写在后面
前言
-
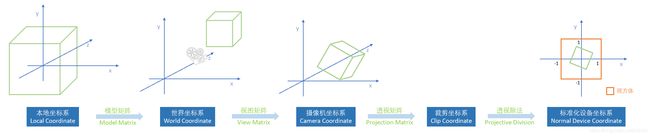
图元装配是图形学渲染管线中很重要的一环。其目的在于将位于模型坐标系下的顶点,通过矩阵运算,最终变换至标准设备坐标系下(NDC);
-
其中模型矩阵和视图矩阵的推导很容易理解,但是透视投影矩阵即使理解了也要每次推导一遍才能确认自己明白了。因此写下这篇博文,帮助自己加深印象。同时也希望它能帮助你理解透视投影矩阵,我会尽量详细地讲解每一个步骤;
-
但是正如你能在其他解释图元装配的文章一样,有必要说明一下——除非你有需要,否则你可以不用关心这些矩阵是怎么来的。当你真正用到它们的时候再去查阅资料也来得及;
-
原创不易,转载请注明出处和作者,谢谢!
前置知识
- 了解透视投影的原理,至少知道视锥体的存在;
- 知道齐次坐标,至少知道w分量的存在;
视见体和标准设备坐标系
为了明白透视投影的目的,有必要先了解什么是视见体和标准设备坐标系:
- 视见体是长度为2、宽度为1、高度为2的一个立方体;
- 标准设备坐标系是 x∈[-1, 1]、y∈[-1, 1]、z∈[0, 1] 的一个坐标系;
如下图所示,正如你所看到的是,视见体往往可以等价于标准设备坐标系:
那么视见体和标准设备坐标系在渲染管线中起到什么作用呢?答案是位于视见体以外的所有顶点会被丢弃(或者说裁剪)掉。换一句话说,渲染管线只会使用坐标位于视见体中的顶点,继续参与后面的渲染过程。
- 需要注意的是不同图形API对视见体的规定不一样,上面的是DirectX3D的标准;而OpenGL的标准对z的要求是[-1, 1]。但是这对透视投影矩阵的推导影响不大;
- 后面的视见体采用的是上面所说的标准。
透视投影
原理
接下来看看透视投影的视锥体,这里借用一段引用来简单解释视锥体1:
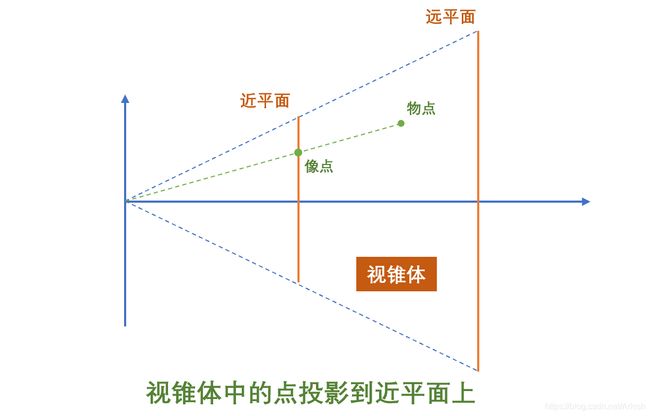
视锥体(frustum)是指场景中摄像机的可见的一个锥体范围。它由上、下、左、右、近、远共6个面组成。在视锥体内的景物可见,反之则不可见。
需要补充的是,视锥体中的景象最后会被被投影到近平面上。这里的视锥体好比如人类的眼球成像原理,物点经过晶状体后投影在视网膜上,人才能看到物体(左图是人眼的成像原理,右图是透视投影的成像原理 ):
目的/结果
从上面的原理中可以看出视锥体和视见体的共同点:
- 渲染管线只会渲染视见体中的内容;
- 视锥体是人为规定的一块区域,希望只能显示这其中的内容。
因此,透视投影矩阵的目的就是通过映射关系,将视锥体区域映射到视见体中。从数学角度上解释,则是为了让视锥体中的点,在经过投影矩阵以后,符合以下公式:
− 1 ≤ X N D C ≤ 1 − 1 ≤ Y N D C ≤ 1 0 ≤ Z N D C ≤ 1 其 中 X N D C , Y N D C , Z N D C 为 视 锥 体 中 的 点 在 N D C 坐 标 系 下 的 坐 标 -1\leq X \scriptsize NDC \normalsize \leq 1 \\ -1\leq Y \scriptsize NDC \normalsize \leq 1 \\ 0\leq Z \scriptsize NDC \normalsize \leq 1 \\ 其中X \scriptsize NDC \normalsize , Y \scriptsize NDC \normalsize , Z \scriptsize NDC \normalsize 为视锥体中的点在NDC坐标系下的坐标 −1≤XNDC≤1−1≤YNDC≤10≤ZNDC≤1其中XNDC,YNDC,ZNDC为视锥体中的点在NDC坐标系下的坐标
透视投影矩阵的推导
有了上面的结论以后,接下来进行推导——设法将一个处于视锥体中的点P,经过一个矩阵,使得其处于视见体范围当中。
- 为了计算和描述方便,我们假设视锥体如下:
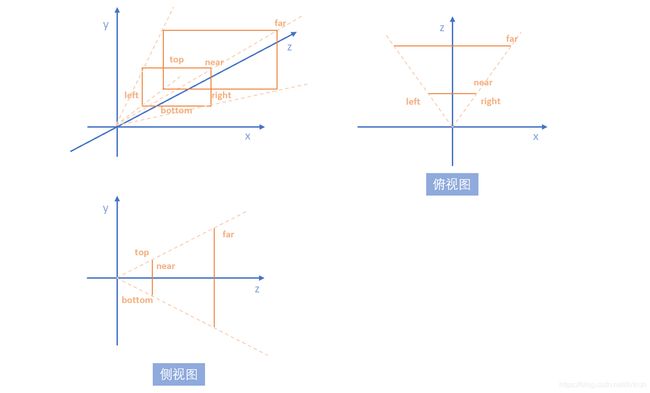
左 面 : l e f t , 右 面 : r i g h t 上 面 : t o p , 下 面 : b o t t o m 近 平 面 : n e a r , 远 平 面 : f a r 左面: left,\ 右面: right\\ 上面: top,\ 下面: bottom\\ 近平面: near, \ 远平面: far 左面:left, 右面:right上面:top, 下面:bottom近平面:near, 远平面:far
即如下图所示:
- 并对计算结果有下面的表示:
视 锥 体 下 点 P f : ( X f , Y f , Z f , 1 ) 近 平 面 下 点 P n : ( X n , Y n , n e a r , 1 ) 投 影 矩 阵 运 算 后 点 P p : ( X p , Y p , Z p , 1 ) f 表 示 f r u s t u m , 表 示 视 锥 体 下 的 点 n 表 示 n e a r , 表 示 近 平 面 下 的 点 p 表 示 p r o j e c t i v e , 表 示 投 影 矩 阵 运 算 后 的 点 视锥体下点P \scriptsize f \normalsize: (X \scriptsize f \normalsize ,Y \scriptsize f \normalsize ,Z \scriptsize f \normalsize ,1 ) \\ 近平面下点P \scriptsize n \normalsize: (X \scriptsize n \normalsize ,Y \scriptsize n \normalsize ,near \normalsize ,1 ) \\ 投影矩阵运算后点P \scriptsize p \normalsize: (X \scriptsize p \normalsize ,Y \scriptsize p \normalsize ,Z \scriptsize p \normalsize ,1 )\\ f表示frustum,表示视锥体下的点\\ n表示near,表示近平面下的点\\ p表示projective,表示投影矩阵运算后的点\\ 视锥体下点Pf:(Xf,Yf,Zf,1)近平面下点Pn:(Xn,Yn,near,1)投影矩阵运算后点Pp:(Xp,Yp,Zp,1)f表示frustum,表示视锥体下的点n表示near,表示近平面下的点p表示projective,表示投影矩阵运算后的点
1. 计算视锥体的点投影到近平面的x、y坐标
前面说过,视锥体中的景象会被投影到近平面。因此我们的第一步就是计算视锥体中的一个点,其投影到近平面的点Pp。
计算原理很简单,我们可以使用相似三角形分别计算得到,如下图所示计算近平面的x坐标:
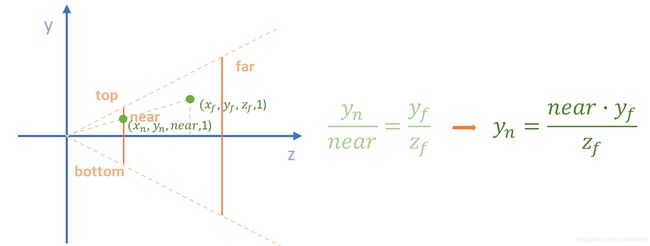
同理通过同样的方法计算近平面的y坐标:
因此我们得到近平面的x、y坐标分别为:
X n = n e a r ⋅ X f Z f Y n = n e a r ⋅ Y f Z f X \scriptsize n \normalsize = \frac {near\cdot X \scriptsize f} {Z \scriptsize f}\\ Y \scriptsize n \normalsize = \frac {near\cdot Y \scriptsize f} {Z \scriptsize f}\\ Xn=Zfnear⋅XfYn=Zfnear⋅Yf
另外,因为它们处于近平面上,因此还符合以下公式:
X n = n e a r ⋅ X f Z f ∈ [ l e f t , r i g h t ] Y n = n e a r ⋅ Y f Z f ∈ [ b o t t o m , t o p ] X \scriptsize n \normalsize = \frac {near\cdot X \scriptsize f} {Z \scriptsize f} \in [left, right] \\ Y \scriptsize n \normalsize = \frac {near\cdot Y \scriptsize f} {Z \scriptsize f} \in [bottom, top]\\ Xn=Zfnear⋅Xf∈[left,right]Yn=Zfnear⋅Yf∈[bottom,top]
- 注意:之所以不需要计算近平面的z坐标,是因为近平面的z都是near
2. 规范化近投影面的x、y坐标
第一步中我们得到了近平面上的x、y坐标。我们的目标是标准化设备坐标系,也就是说要将 [ left, right ]映射到 [ -1, 1 ]。
这不难做到,下面以Xn为例:
l e f t ≤ X n = n e a r ⋅ X f Z f ≤ r i g h t left \leq X \scriptsize n \normalsize = \frac {near\cdot X \scriptsize f} {Z \scriptsize f} \leq right left≤Xn=Zfnear⋅Xf≤right
首先两边同时减去left:
0 ≤ n e a r ⋅ X f Z f − l e f t ≤ r i g h t − l e f t 0 \leq \frac {near\cdot X \scriptsize f} {Z \scriptsize f} - left \leq right - left 0≤Zfnear⋅Xf−left≤right−left
接着两边同时乘2后除以(right-left):
0 ≤ 2 ⋅ n e a r ⋅ X f Z f ⋅ ( r i g h t − l e f t ) − 2 ⋅ l e f t ( r i g h t − l e f t ) ≤ 2 0 \leq \frac {2 \cdot near\cdot X \scriptsize f} {Z \scriptsize f \normalsize \cdot (right - left)} - \frac {2 \cdot left} {(right - left)} \leq 2 0≤Zf⋅(right−left)2⋅near⋅Xf−(right−left)2⋅left≤2
最后两边同时减去1,这个映射就完成了:
− 1 ≤ 2 ⋅ n e a r ⋅ X f Z f ⋅ ( r i g h t − l e f t ) − r i g h t + l e f t ( r i g h t − l e f t ) ≤ 1 -1 \leq \frac {2 \cdot near\cdot X \scriptsize f} {Z \scriptsize f \normalsize \cdot (right - left)} - \frac {right + left} {(right - left)} \leq 1 −1≤Zf⋅(right−left)2⋅near⋅Xf−(right−left)right+left≤1
Yn通过同样的计算过程也可以进行规范化,这里就省略过程了:
− 1 ≤ 2 ⋅ n e a r ⋅ Y f Z f ⋅ ( t o p − b o t t o m ) − t o p + b o t t o m ( t o p − b o t t o m ) ≤ 1 -1 \leq \frac {2 \cdot near\cdot Y \scriptsize f} {Z \scriptsize f \normalsize \cdot (top - bottom)} - \frac {top + bottom} {(top - bottom)} \leq 1 −1≤Zf⋅(top−bottom)2⋅near⋅Yf−(top−bottom)top+bottom≤1
我们得到了规范化后的x、y坐标。因为它们位于标准化设备坐标系下,所以它们应该是投影矩阵运算后的结果,也就是Xp、Yp:
X p = 2 ⋅ n e a r ⋅ X f Z f ⋅ ( r i g h t − l e f t ) − r i g h t + l e f t r i g h t − l e f t Y p = 2 ⋅ n e a r ⋅ Y f Z f ⋅ ( t o p − b o t t o m ) − t o p + b o t t o m t o p − b o t t o m X \scriptsize p \normalsize = \frac { 2 \cdot near\cdot X \scriptsize f} {Z \scriptsize f \normalsize \cdot (right - left)} - \frac {right + left} {right - left}\\ Y \scriptsize p \normalsize = \frac { 2 \cdot near\cdot Y \scriptsize f} {Z \scriptsize f \normalsize \cdot (top - bottom)} - \frac {top + bottom} {top - bottom} Xp=Zf⋅(right−left)2⋅near⋅Xf−right−leftright+leftYp=Zf⋅(top−bottom)2⋅near⋅Yf−top−bottomtop+bottom
但是这里有一个问题是,我们无法将这个Xp关于Xf(Xp关于Yf)的公式写成一个矩阵,因为矩阵变换是线性的——换一句话说,我们希望Xp、Yp是形如下面所示的公式:
X p = a X f + b Y f + c Z f + d Y p = a X f + b Y f + c Z f + d X \scriptsize p \normalsize = aX \scriptsize f \normalsize +bY \scriptsize f \normalsize +cZ \scriptsize f \normalsize + d \\ Y \scriptsize p \normalsize = aX \scriptsize f \normalsize +bY \scriptsize f \normalsize +cZ \scriptsize f \normalsize + d Xp=aXf+bYf+cZf+dYp=aXf+bYf+cZf+d
很明显我们得到的Xp、Yp由于分母有Zf的缘故,导致了这个公式是非线性的。为了使公式线性,我们可以再采取两边同时乘以Zf的策略,得到的结果如下。但正如你所看到的,现在它又不符合标准化设备坐标系了:
− Z f ≤ X p = 2 ⋅ n e a r ⋅ X f r i g h t − l e f t − Z f ⋅ r i g h t + l e f t r i g h t − l e f t ≤ Z f − Z f ≤ Y p = 2 ⋅ n e a r ⋅ Y f t o p − b o t t o m − Z f ⋅ t o p + b o t t o m t o p − b o t t o m ≤ Z f -Z \scriptsize f \normalsize \leq X \scriptsize p \normalsize = \frac { 2 \cdot near\cdot X \scriptsize f} { right - left} - Z \scriptsize f \normalsize \cdot \frac {right + left} {right - left} \leq Z \scriptsize f \normalsize\\ -Z \scriptsize f \normalsize \leq Y \scriptsize p \normalsize = \frac { 2 \cdot near\cdot Y \scriptsize f} { top - bottom} - Z \scriptsize f \normalsize \cdot \frac {top + bottom} {top - bottom} \leq Z \scriptsize f \normalsize\\ −Zf≤Xp=right−left2⋅near⋅Xf−Zf⋅right−leftright+left≤Zf−Zf≤Yp=top−bottom2⋅near⋅Yf−Zf⋅top−bottomtop+bottom≤Zf
似乎陷入了困境,我们无法继续推导出投影矩阵。
3. 透视除法消除非线性变换
办法还是有的,而且渲染管线已经帮我们想好解决方案,那就是透视除法。所谓透视除法,其实就是在图元装配最后,渲染管线会将这个顶点的xyzw值除以w值。例如有点A,那么它透视除法以后如下所示:
点 A : ( x , y , z , w ) 透 视 除 法 后 : ( x w , y w , z w , 1 ) 点A:(x, y, z, w)\\ 透视除法后:(\frac x w, \frac y w, \frac z w, 1) 点A:(x,y,z,w)透视除法后:(wx,wy,wz,1)
看到这里你可能已经明白上面的问题要怎么解决了——我们设法将w分量变换为Zf,那么透视除法后又能使上面的Xp、Yp符合标准化设备坐标系。
而且也不难通过矩阵将w分量变换为z分量,如下面所示:
( x , y , z , 1 ) [ 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 ] = ( x , y , z , z ) (x, y, z, 1) \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix} = (x, y, z, z) (x,y,z,1)⎣⎢⎢⎡1000010000100010⎦⎥⎥⎤=(x,y,z,z)
4. 计算视锥体的点投影后的深度(z)
我们已经解决了Xp、Yp的计算。接下来我们来考虑Zp——也就是视锥体中的点经过投影矩阵变换后的Z(也称作深度)。因为Zp不依赖于x、y,所以我们的目标是找到一个Zp关于Zf的线性公式满足:
Z p = k Z f + b Z \scriptsize p \normalsize = k Z \scriptsize f \normalsize + b Zp=kZf+b
那么应该怎么求这个公式呢?实际上我们知道(near, 0)和(far, far)一定满足这条公式。
- (near, 0)很好理解,Zf为near时应该映射到0的位置;
- (far, far)本质上和上面一样,Zf为far时应该映射到1的位置。但可别忘了要考虑透视除法,所以应该是(far, far)而不是(far, 1);
将这两个点带入公式我们可以求得k和b,如下所示:
k = f a r f a r − n e a r b = − n e a r ⋅ f a r f a r − n e a r Z p = f a r f a r − n e a r Z f − n e a r ⋅ f a r f a r − n e a r k = \frac {far} {far - near}\\ b = \frac {-near \cdot far} {far - near}\\ Z \scriptsize p \normalsize = \frac {far} {far - near}Z \scriptsize f \normalsize - \frac {near \cdot far} {far - near} k=far−nearfarb=far−near−near⋅farZp=far−nearfarZf−far−nearnear⋅far
5. 得到透视投影矩阵
很好,前面我们已经推导出Xp、Yp、Zp,它们分别如下所示:
X p = 2 ⋅ n e a r r i g h t − l e f t X f − r i g h t + l e f t r i g h t − l e f t Z f Y p = 2 ⋅ n e a r t o p − b o t t o m Y f − t o p + b o t t o m t o p − b o t t o m Z f Z p = f a r f a r − n e a r Z f − n e a r ⋅ f a r f a r − n e a r X \scriptsize p \normalsize = \frac { 2 \cdot near } { right - left} X \scriptsize f \normalsize - \frac {right + left} {right - left} Z \scriptsize f \normalsize \\ Y \scriptsize p \normalsize = \frac { 2 \cdot near} { top - bottom} Y \scriptsize f \normalsize - \frac {top + bottom} {top - bottom} Z \scriptsize f \normalsize \\ Z \scriptsize p \normalsize = \frac {far} {far - near}Z \scriptsize f \normalsize - \frac {near \cdot far} {far - near} Xp=right−left2⋅nearXf−right−leftright+leftZfYp=top−bottom2⋅nearYf−top−bottomtop+bottomZfZp=far−nearfarZf−far−nearnear⋅far
它们都是线性的,很容易得到下面的矩阵,它就是透视投影矩阵(注意这里使用行主序,即使用行向量的点左乘矩阵):
[ 2 ⋅ n e a r r i g h t − l e f t 0 0 0 0 2 ⋅ n e a r t o p − b o t t o m 0 0 − r i g h t + l e f t r i g h t − l e f t − t o p + b o t t o m t o p − b o t t o m f a r f a r − n e a r 1 0 0 − n e a r ⋅ f a r f a r − n e a r 0 ] \begin{bmatrix} \frac { 2 \cdot near } { right - left} & 0 & 0 & 0 \\ 0 & \frac { 2 \cdot near} { top - bottom} & 0 & 0 \\ -\frac {right + left} {right - left} & -\frac {top + bottom} {top - bottom} & \frac {far} {far - near} & 1 \\ 0 & 0 & - \frac {near \cdot far} {far - near} & 0 \end{bmatrix} ⎣⎢⎢⎢⎡right−left2⋅near0−right−leftright+left00top−bottom2⋅near−top−bottomtop+bottom000far−nearfar−far−nearnear⋅far0010⎦⎥⎥⎥⎤
- 注意:第三行第四列的元素是1,这就是刚才所说的要将w分量变换为z分量,以配合透视除法。
写在后面
- 计算机图形学可以说都是由数学组成的,因此想要深入学习那么数学一定不能落下。在这里督促一下自己后面一定要补习3D数学;
- 是这篇文章让我真正认识到投影矩阵以及透视除法的作用,感谢原作者以及译者:原文章 翻译
- 后续我会进一步编写图元装配中其他矩阵推导和原理的博文!
- 最后宣传一下最近新创建的公众号。我的想法是致力于分享实用的、有趣的干货,希望我能贯彻到底,也衷心希望它们能帮助到你!(目前还没有发布文章,近期应该会将博文转到公众号)
https://www.cnblogs.com/dragon2012/p/3891519.html ↩︎