HIT 软件构造2019春 Lab6

update 6/4/2019

 

问题解决

 

线程关闭问题

  实验中，采用

       ScheduleExecutorService service = Executors.newSingleThreadScheduledExecutor()

       Service.scheduleAtFixedRate

  实现定时任务，我们需要这个定时任务达到一定条件就停止，比如过河线程等猴子过河之后停止。停止定时任务的方法有两个关键步骤，一是Future.cancel，一是service.shutdown，只调用Future.cancel的话定时任务会停止，但是线程依然存在，程序不会停止。

  以下是过河线程示例：

final String jobId = "startCrossRiverThread";
    final Map futureMap = new HashMap<>();
    Future future = service.scheduleAtFixedRate(() -> {

      //  过河线程
      if (state.state == 1) {
        Ladder ladder = strategy.assign(this);
        if (ladder != null) {
          nextStep();
        }
        state.increaseLifeTime(1);
        logger.info(state.toString());
      } else if (state.state == 2) {
        nextStep();
        state.increaseLifeTime(1);
        logger.info(state.toString());
      } else if (state.state == 3) {
        //所有猴子都已经过河，计算吞吐率、公平性
        if(generator.crossedCount == generator.N) {
          generator.getInfoOfGame();
        }
        futureMap.get(jobId).cancel(true);
        service.shutdown();
      }


    }, 0, MonkeyGenerator.STEPTIME, TimeUnit.MILLISECONDS);
    futureMap.put(jobId, future);

 

JFreeChart图表比较

  对多个算法、多个文件计算最终吞吐率、合法性。

  首先需要创建多个Generator实例，在一个Generator中完成对一个文件一个算法的测试，因此这里同时存在着多个线程“组”，只有当所有的线程都完成计算的时候我们才能得到所有的吞吐率、合法性信息--DefaultCategoryDataset，并依此来创建图表。这里使用CountDownLatch实现阻塞主线程等待所有线程“组”执行完成的功能。

 

 

实验报告

 

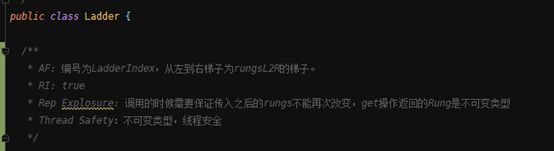
1. 1. ADT设计方案

Rung-踏板:

域名	作用
rungIndex	踏板所处的位置（从左到右）

 

方法名	作用
getRungIndex	获得踏板的位置

 

Specification：

 

Ladder-梯子：

域	作用
ladderIndex	梯子的编号
List rungL2R	从左到右梯子上的所有踏板

 

方法	作用
Public Rung getRungL2R(int rungIndex)	获得从左到右数第rungIndex个踏板
Public Rung getRungR2L(int rungIndex)	获得从右到左数第rungIndex个踏板
Public int getRungLength()	获得梯子上踏板的总数
Pubic int getLadderIndex()	获得当前梯子的编号

Specification：

 

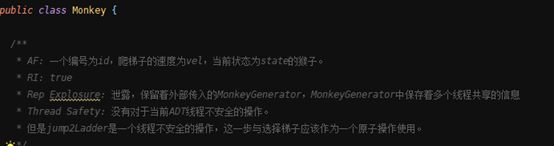
Monkey-猴子：

域名	作用
List crossriverStrategies	该猴子可以使用的过河策略
Int id	猴子id
Int vel	猴子过河速度
MonkeyState state	猴子状态
MonkeyGenerator generator	保留的MonkeyGenerator的引用

 

方法	作用
Public void startCrossRiverThread	启动该猴子的过河线程
Public void Jump2Ladder(Ladder ladder)	该猴子跳至Ladder的第一个踏板上，这一步不需要消耗时间
Public void nextStep()	处于梯子上的猴子走出下一步
Getter for reps

 

 

MonkeyState-内部类-猴子状态

域名	作用
Int id	猴子id
String direction	猴子方向
Int state	当前猴子状态，猴子一共有三个状态，分别是state1-在原地等待，state2-处于梯子上，state3-已经到达对岸
Ladder ladder	如果当前猴子处于state2 则保存猴子所处的梯子
Rung rung	如果当前猴子处于state2 则保存猴子所处的梯子的踏板
Int lifetime	猴子活了多长时间
Int borntime	猴子出生的时间点

 

Pubic void nextState	对当前的猴子进行状态转移，转移到下一个状态
Public void setLocation(Ladder ladder,Rung rung)	设置state2的猴子的所处的位置，这一步需要在执行nextState操作之前进行
Public void increaseLifeTime(int inctime)	将当前猴子的生存时间加上inctime
Public Sting toString()	覆盖toStirng，按照文档中指定的格式返回当前猴子的状态

 

Specification：

 

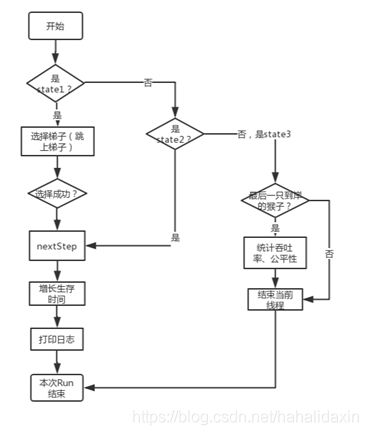
1. 1. Monkey线程的run()的执行流程图

解释：

nextStep：在梯子上的猴子进行下一步动作，首先加锁，猴子进行下一步需要考虑前一个猴子（如果有）、梯子总数、自己能走多远，最终根据行进方向走出这一步。

1. 1. 至少两种“梯子选择”策略的设计与实现方案
      1. 策略1

1. 1. 1. 策略2

1. 1. 1. 策略3（可选）

SmartStrategy：

       三种策略的总体流程都是相同，都是先将梯子到猴子的映射上锁，首先找出所有可以上的梯子，需要满足梯子上猴子的行进方向与“我”相同、梯子上第一个踏板为空（按照行进方向的第一个，需要区别行进方向）。

将猴子的速度划分为三个等级，分别是低速度猴子（=MIDSPEED)，对于低速度猴子（心有B树）不会去抢占一个空的梯子，对于中速度、高速度猴子，会优先抢占空的梯子，只要保证中、高速度猴子不空则一定能保证低速度猴子移动。对于中、低速度猴子，选择队列中最后一个猴子离“我”最近的梯子，这样可以相对保证该猴子的速度对后面猴子的影响较小，对于高速度猴子，选择队列中最后一个猴子离“我”最远的梯子，这样可以使高速度猴子尽快追上最后一个猴子，有效减少梯子上空余的踏板。

1. 1. “猴子生成器”MonkeyGenerator

使用

ScheduleExecutorService service = Executors.newSingleThreadScheduledExecutor()

Service.scheduleAtFixedRate

创建一个定时任务，每隔t*STEPTIME执行一次。这里的STEPTIME是指刷新的单位时间，所有的定时任务都以TIMESTEP作为单位刷新时间，这样如果想要快速跑出结果只需要减小TIMESTEP即可。

对于每一次定时任务，按照要求生成k个猴子，对于每个猴子在范围内随机生成参数，将该猴子添加到猴子列表中，然后启动猴子的过河线程。

所有猴子线程共享的数据作为public数据直接保存在MonkeyGenerator中，在猴子的构造函数中需要将MonkeyGenerator作为参数传入，这样就可以直接通过引用访问多线程共享的数据。

1. 1. 如何确保threadsafe？

  多线程可能产生问题的地方在多个猴子可能同时想要进行选择梯子和猴子前进下一步的时候。

  对于猴子上梯子操作，包括选梯子和上梯子两个步骤，这两个步骤必须作为一个原子操作，所以同一时刻只能安排有一只猴子上梯子，在本实验中，请求Map>的锁。同时考虑到在第一个踏板上的猴子会行进的问题，（假设这是个<足够聪明、动作敏捷>的猴子），所以在考虑梯子的时候还需要请求梯子的锁。

  对于猴子在梯子上行进的过程中，一个猴子移动包括根据形势作出判断、移动两个操作，为了保证这是个<足够聪明、动作敏捷>的猴子，这里将这两个步骤作为一个原子操作，这里选择请求猴子所在梯子的锁。

       其实，如果是个傻猴，我们完全没有必要请求梯子的锁，这并不会产生线程安全问题。

       另外，对于多线程共享的数据结构还需要考虑使用线程安全的类型或者请求锁的方式来保证一般操作的线程安全。

 

1. 1. 系统吞吐率和公平性的度量方案

对于吞吐率、公平性的定义完全依照实验要求。

       如何实现计算吞吐率和公平性？在MonkeyGenerator（储存线程共享数据）中添加一个到岸猴子计数器，当最后一个猴子达到对岸的时候计算吞吐率和公平性。

       关于时间统计，每一个猴子都有一个计数器lifetime，过河线程每执行一次 他的时间都会续一秒 ，所有猴子过河的时间就是最大的borntime+lifetime。所以本程序吞吐率完全依赖于上梯子策略的选择。

1. 1. 输出方案设计

日志：

       日志输出格式按照实验报告要求完成。如图：

      

 

GUI

       猴子过河图：左右两边是等待的猴子，中间是梯子，一只猴子用 [id,vel] 来代表。右边即时显示已经过河的猴子数目。

 

       过河完成图：当过河完成时，右边显示出吞吐率和公平性

1. 1. 猴子过河模拟器v1
      1. 参数如何初始化

使用配置文件的方式设置好初始化参数，程序中只需要从配置文件中读入即可。配置文件位于src/resources/configfiles。

1. 1. 1. 使用Strategy模式为每只猴子选择决策策略

设计Interface CrossriverStrategy，提供函数Ladder assign(Monkey monkey)，monkey按照既定策略选择一个可用的梯子，如果有，则跳上梯子的第一个踏板。

因为选梯子过程中涉及到访问线程共享数据，所以每一个实现类都需要在构造方法中传入MonkeyGenerator的引用。

1. 1. 猴子过河模拟器v2
      1. 对比分析：固定其他参数，选择不同的决策策略
      2. 对比分析：变化某个参数，固定其他参数
      3. 分析：吞吐率是否与各参数/决策策略有相关性？

下面对三个要求统一分析：

说明：

              SimpleStrategy：策略1

              PushspeedStrategy：策略2

              SmartStrategy：策略3

              f1->f5中参数按照从小到大变化。

              报告中选用的都是多次试验之后能够代表普遍规律的图。

 

       以下报告中的SmartStrategy没有人工调整参数，参数保持不变（LOWSPEED=2，MIDSPEED=4）。

 

EXP1：

实验数据：

参数	n	h	t	N	k	MV
取值	1-5	20	3	100	3	5

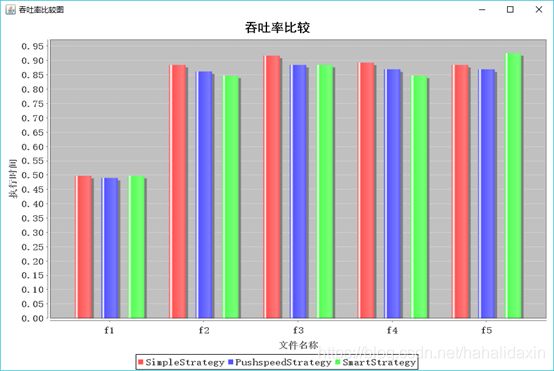
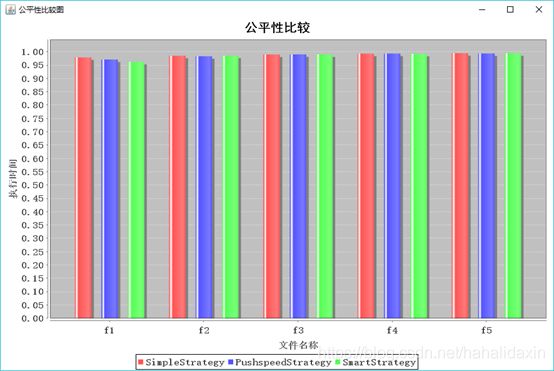
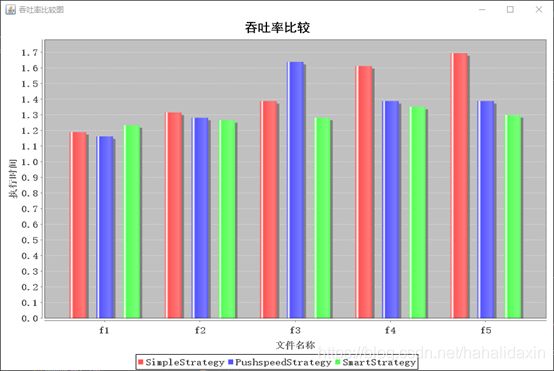
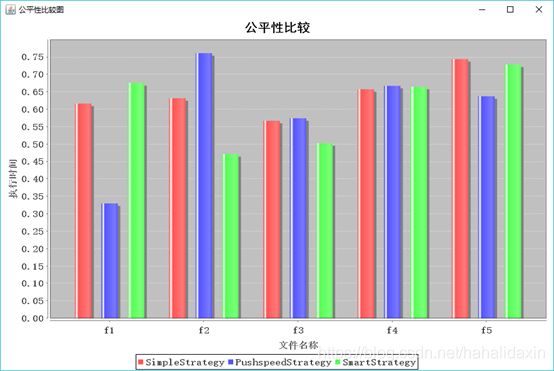
实验结果：

 

分析结果：

随着梯子数目n的增加，首先从n=1变化到n=2吞吐率得到很大提高，在n=2到n=5的变化中，吞吐率变化不大。对于公平性，规律类似。说明三种策略对于增加梯子的利用效率不高。

与具体算法策略关系不大。

 

EXP2：

 

实验数据：

参数	n	h	t	N	k	MV
取值	3	20	1-5	100	3	8

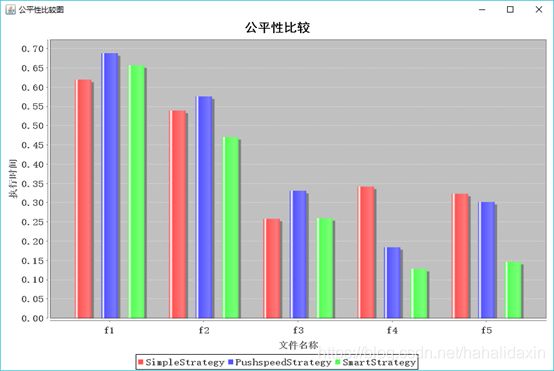
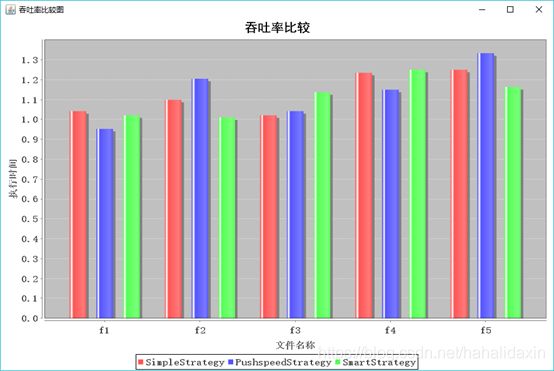
实验结果：

 

结果分析：

随着生猴子间隔时间t的增加，吞吐率总体降低，公平性总体提高。生猴子频率太低密度太小，不能很好利用梯子。

与具体算法策略关系不大。

 

EXP3：

实验数据：

参数	n	h	t	N	k	MV
取值	3	20	3	200,400,…,1000	3	50

实验结果：

 

结果分析：

随着生猴子总数的上升，吞吐率与公平性整体变化不大。当生猴子总数非常大的时候，主要是生猴子的频率与密度在起着影响。

与具体算法策略关系不大。SimpleStrategy始终较低。

 

EXP4：

实验数据：

参数	n	h	t	N	k	MV
取值	3	20	3	100	6,12,24,36,48	10

实验结果：

 

结果分析：

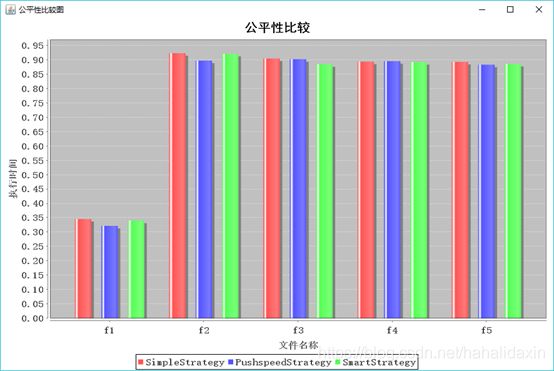
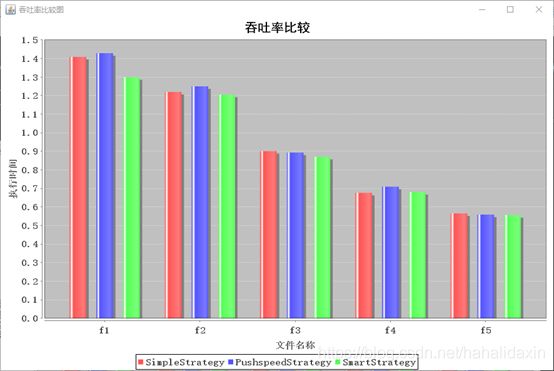
随着每轮生的猴子的数目的增加，吞吐率整体上升，公平性整体下降。猴子密度提上去，有效利用了梯子。

吞吐率而言在f2之后SimpleStrategy总体高于其他两个。

      

 

EXP5：

实验数据：

参数	n	h	t	N	k	MV
取值	3	20	3	100	6	2,4,6,8,10

实验结果：

 

结果分析：

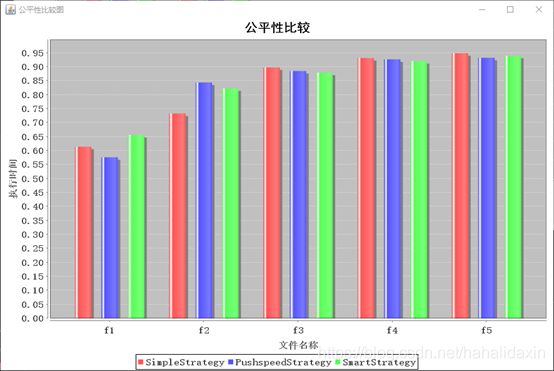
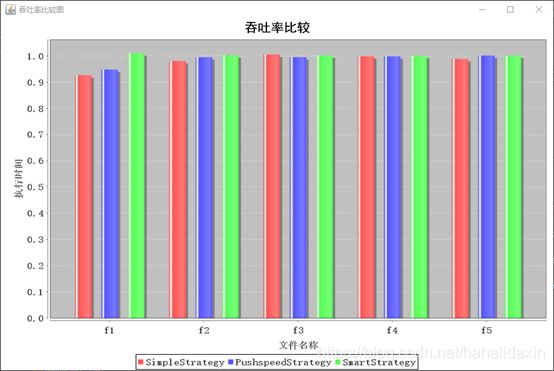
随着最大速度的提高，吞吐率整体上升，公平性规律不明显。速度提高了，自然总体跑得快了。

算法比较总体规律不明显。

 

1. 1. 1. 压力测试结果与分析

压力测试1：

实验数据：

参数	n	h	t	N	k	MV
取值	2	20	1	1000	25	10

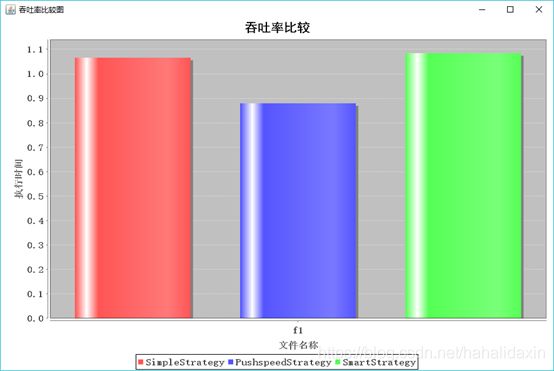
实验结果：

 

结果分析：

吞吐率比较低，公平性差。

算法对比， PushspeedStrategy吞吐率低于其他两个算法，公平性较好。

 

压力测试2：

实验数据：

参数	n	h	t	N	k	MV
取值	2	2000	3	100	5	100

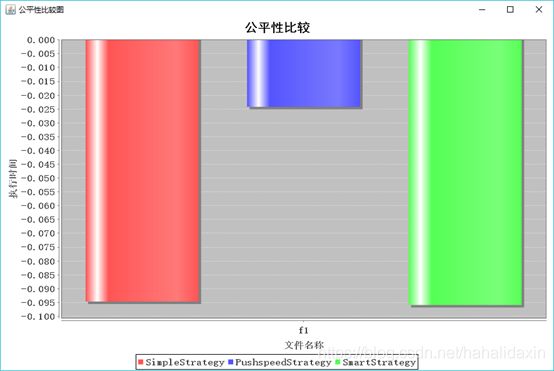
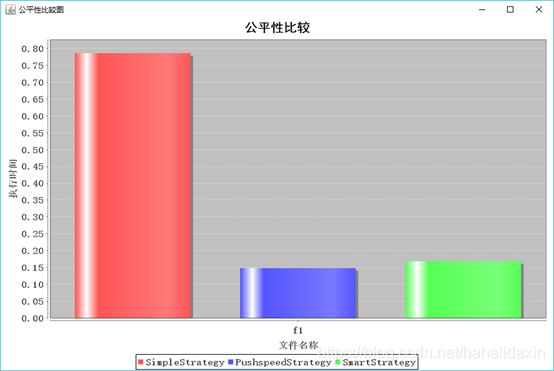
实验结果：

 

结果分析：

       吞吐率极低。

       PushspeedStrategy吞吐率表现较好，SimpleStrategy公平性表现较好。

 

1. 1. 猴子过河模拟器v3

以下只针对SmartStrategy记录结果，对于三个文件，参数设置如下：

LOWSPEED=2,MIDSPEED=4

LOWSPEED=3,MIDSPEED=5

LOWSPEED=1,MIDSPEED=3

 

	吞吐率	公平性
Competiton_1.txt
第1次模拟	2.400000	0.557770
第2次模拟	2.238806	0.204593
第3次模拟	2.325581	0.500691
第4次模拟	2.400000	0.499220
第5次模拟	2.380952	0.482453
第6次模拟	2.307692	0.383099
第7次模拟	2.325581	0.490792
第8次模拟	2.362205	0.493378
第9次模拟	2.419355	0.505329
第10次模拟	2.419355	0.528161
平均值	2.357953	0.464549
Competiton_2.txt
第1次模拟	5.102041	0.476248
第2次模拟	5.102041	0.583856
第3次模拟	4.950495	0.470942
第4次模拟	4.854369	0.480257
第5次模拟	5.208333	0.600737
第6次模拟	5.050505	0.440176
第7次模拟	4.854369	0.555880
第8次模拟	5.050505	0.466437
第9次模拟	4.901961	0.491094
第10次模拟	4.901961	0.512641
平均值	4.997658	0.507827
Competiton_3.txt
第1次模拟	1.136364	0.263434
第2次模拟	1.111111	0.201616
第3次模拟	1.111111	0.262222
第4次模拟	1.111111	0.277980
第5次模拟	1.111111	0.257374
第6次模拟	1.063830	0.320404
第7次模拟	1.075269	0.264242
第8次模拟	1.123596	0.230707
第9次模拟	1.063830	0.303030
第10次模拟	1.123596	0.260202
平均值	1.103093	0.264261

 

 

                                    我是迷人的小尾巴

---

以下外链，利益相关，欢迎浏览ε≡٩(๑>₃<)۶ ：

济南江鹏工贸有限公司（山东济南机械加工），济南彤昌机械科技有限公司（山东济南机械加工）