多变量微积分笔记（2）——多元函数及其微分

本博客对应我博客中的 多变量微积分目录下的第二章，多元函数及其微分。

2. 多元函数及其微分——单变量函数的延拓

2.1 多元函数

多元函数一般是指某个定义域为 $D$ 的函数 $f$ 有两个及以上的自变量，$z=f(x_1,x_2,x_3,...)$，18.02这门课一般研究含有两个或三个的函数。
（严谨的定义请参见百度百科多元函数词条，或相关参考书）

举两个例子:
$$f(x,y)=x^2+y^2$$$$f(x,y,z)=xy\log (z)$$

自变量和因变量（Independent and Dependent Variables）

如果函数的表达式为 $z=f(x_1,x_2)$，则$x_1,x_2$被称为函数的自变量，因为他们可以取定义域内的任意值，而因变量 $z$ 会随着自变量取值的变化而变化。

如何简单画多元函数的草图（Sketch）

由于受维度的限制，一般情况我们只能画出二元函数 $f(x,y)$ 的图像和三元函数等值面 $f(x,y,z)=C$ 的图像（等值面下一节会写到）

一般步骤为：

1. 先画出坐标轴 $x,y,z$，常用右手坐标系
2. 固定 $y=a$，一般我们选最简单的情况 $y=0$，画出 $xz$ 平面上的图像；同理，固定 $x=0$，我们可以得到$yz$平面上的图像。
3. 之后，令$z=a$，$a$ 为任意常数（$z=a$经常被称为等高线）

比如，效仿以上步骤我们可以画出$f(x,y)=x^2+y^2$的图像：

2.2 直观认识多元函数——等高线、等值面（Contour Plots and Level Surface）

等高线和等值面

等值面是由一个函数固定其因变量的值而得到的，比如在二元函数$z=f(x,y)$中就是固定$z$的值，然后画出其 $xy$ 平面上的曲线，如果将每一个固定$z$的值之后得到的曲线画在一起，就得到了等高线图。

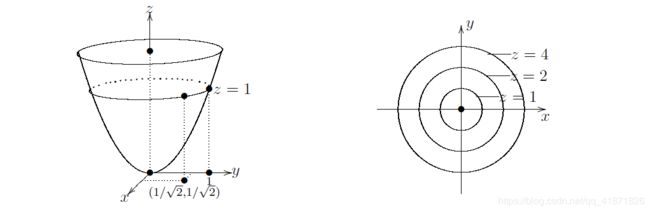
如图，当$z=4$得到的圆盘就是等值面（level curves），而整个由各个圆盘组成的图像被称为等高线图。也可以认为等高线就是从上往下切割，并做出其在水平面上的投影。

2.3 多元函数的偏导数

偏导数的定义：（对于二元函数来说）

令$w=f(x,y)$是一个二元函数，它的关于 $x$ 的偏导数表示为：
$$\frac{\partial f}{\partial x}{|}_{(x_0,y_0)}or\frac{\partial f(x,y_0)}{\partial x}{|}_{x_0}or{f}_x(x_0,y_0)$$
同理，关于 $y$ 的偏导数为:
$$\frac{\partial f}{\partial y}{|}_{(x_0,y_0)}or\frac{\partial f(x_0,y)}{\partial x}{|}_{y_0}or{f}_y(x_0,y_0)$$
三元甚至多元函数的偏导数也同理。

在单变量微积分中，函数的导数只针对一个方向；而在多元函数当中，求导数需要参考某一个方向，做一个类比，在爬山的时候，沿着你的正面或侧面望去，山的陡峭程度是不同的。同理，在求多元函数的导数必须要声明导数是参考于哪个方向，即针对哪个变量。

切面近似——偏导数的重要性（Tangent Plane Approximation）

对于单变量函数来说，通过线性近似我们得到了一元函数的微分形式：
$$y+dy=f(x_0)+f^{\prime }(x_0)dxordy=f^{\prime }(x)dx$$
通过类比，对于二元函数来说，我们会立马想到用切面来近似二元函数某一点的值。二元函数某一点$(x_0,y_0,w_0),(w_0=f(x_0,y_0))$的切面要包含该函数在这一点的两条切线，同时我们设这个平面的方程为：
$$A(x-x_0)+B(y-y_0)+C(w-w_0)=0$$$$w-w_0=-\frac{A}{C}(x-x_0)-\frac{B}{C}(y-y_0)$$
这是标准的三维坐标下的平面方程（两个垂直向量的点乘为0）。通过上面的图像我们知道，在$y$固定为常数的时候有：
$$w=w_0+f_x(x_0,y_0)(x-x_0)$$
同理，在$x$固定的时候有
$$w=w_0+f_y(x_0,y_0)(y-y_0)$$
让该平面方程中的 $x=x_0$（得到该切面与$x=x_0$平面的交线），得到 $w-w_0=-\frac{B}{C}(y-y_0)$；让该平面方程中的 $y=y_0$（得到该切面与$y=y_0$平面的交线），得到 $w-w_0=-\frac{A}{C}(x-x_0)$，通过恒等关系，可以得到：
$$\frac{A}{C}=-f_x,\frac{B}{C}=-f_y$$切平面的表达式就变成了$$w-w_0=f_x(x-x_0)+f_y(y-y_0)$$
如果令$x_0=y_0=0$，则切面近似就是：
$$w=f(0,0)+f_x(x)+f_y(y)$$
通过切面的近似我们就能得到多元函数的微分形式，该表达式是多变量微积分中最重要的公式。

2.4 多元函数的微分

多元函数的微分和链式法则

从上一节可以看出，切面近似公式当中蕴含着函数变化量与它的偏导数之间的关系。如果偏导数$f_x,f_y$在点$(x_0,y_0)$附近是连续的，则令$w-w_0=\Delta w,y-y_0=\Delta y,x-x_0=\Delta x$就可以得到多元函数的变化量：
$$\Delta w\approx f_x\Delta x+f_y\Delta y$$
其对应的微分形式就是：
$$dw=f_{x}dx+f_{y}dy$$
同理，对三元函数$w=f(x,y,z)$来说，
$$dw=f_{x}dx+f_{y}dy+f_{z}dz$$
对多元函数$w=f(x_1,x_2,x_3,x_4\cdots )$来说，
$$dw=f_{x_1}d{x}_1+f_{x_2}d{x}_2+f_{x_3}d{x}_3+f_{x_4}d{x}_4+\cdots$$

与学习单变量微积分的时候一样，我们不仅关注函数值的微分随其固有的自变量的变化，还关注参数化（常见的参数化有将自变量表达为随时间变化的函数）之后的微分形式，通过变化后的微分形式我们就得到了新的偏导数表达形式，也就是链式法则。(注意符号$\partial$和$d$没有本质上的区别，都表示微分)

如果函数 $w=f(x,y)$ 的自变量$x,y$在参数化之后能写成$x=x(u,v),y=y(u,v)$的形式，其偏导数形式就变成了：
$$\frac{\partial w}{\partial u}=\frac{\partial f}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial u}$$$$\frac{\partial w}{\partial v}=\frac{\partial f}{\partial x}\frac{\partial x}{\partial v}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial v}$$
三元及三元以上的函数也同样遵循链式法则。

微分与向量的结合——梯度与方向导数

A. 梯度（Gradient）

在上述的微分形式中，我们见到了熟悉的乘法和加法形式（$dw=f_{x}dx+f_{y}dy+f_{z}dz$，其中三元函数$w=f(x,y,z)$），转化成向量点乘的写法就得到：$$dw=<f_x,f_y,f_z>\cdot <dx,dy,dz>$$
其中，$\nabla f=<f_x,f_y,f_z>$被定义为函数$w(x,y,z)$的梯度，$f_x$是$\frac{\partial f}{\partial x}$的简写。$d\mathbf{r}=<dx,dy,dz>$，这也就是方向向量的微分。微分就可以被重写成:
$$dw=\nabla f\cdot d\mathbf{r}$$
通常梯度经常与参数化曲线相结合（常见的是用参数$t$），微分形式为:
$$\frac{dw}{dt}=f_x\frac{dx}{dt}+f_y\frac{dy}{dt}+f_z\frac{dz}{dt}$$$$\frac{dw}{dt}=\nabla f\cdot \frac{d\mathbf{r}}{dt}$$
其中，$$\frac{d\mathbf{r}}{dt}=<\frac{dx}{dt},\frac{dy}{dt},\frac{dz}{dt}>$$
从某种意义来说，这个式子简化了微分的写法。

梯度的性质

梯度一定与函数的等值面的切线垂直

思路及推导：
上文在函数$w=f(x,y,z)$，注意是整个维度上的$w$来明确了梯度的定义，如果函数$w$是个定值（即函数$w$的一个等值面），也就是在$w=f(x,y,z)=C$（即$w$为常数）且$\mathbf{r}$在是等值面或等值面的一条切线（这里考虑的是三元函数，所以$\mathbf{r}$为等值面内的一条切线）的情况下重新推导微分形式。
$$\because \frac{dw}{dt}=\nabla f\cdot \frac{d\mathbf{r}}{dt}\text{and}\frac{dw}{dt}=\frac{dw(x,y,z)}{dt}=\frac{C}{dt}=0$$$$\therefore \nabla f\cdot \frac{d\mathbf{r}}{dt}=\nabla f\cdot \mathbf{v}=0$$
可以看出，$\mathbf{v}$就是等值面的切线，所以结论有梯度一定与函数等值面的切线垂直。

B. 方向导数

当提到梯度的时候，就会立即想到梯度的方向是确定的，即垂直于函数等值面的切线的。而任意方向的导数则需要对上文的推导做一些改进，这时我们放弃$w=f(x,y,z)=C$的假设并令$\mathbf{r}$是函数图像上任意一条曲线，也就是$\frac{dw}{dt}̸=0$。这时
$$\frac{dw}{dt}=\nabla f\cdot \frac{d\mathbf{r}}{dt}=|\nabla f||\frac{d\mathbf{r}}{dt}|\cos \theta =|\nabla f||\mathbf{v}|\cos \theta$$
又因为速度$|\mathbf{v}|=\frac{ds}{dt}$，所以我们就可以得到只包含梯度和与方向向量微分的夹角 $\theta$ 的方程：
$$\frac{\frac{dw}{dt}}{\frac{ds}{dt}}=\frac{dw}{ds}=|\nabla f|\cos \theta =\nabla f\cdot \mathbf{u}<|\nabla f|$$
其中$\mathbf{u}$为曲线$\mathbf{r}$的单位方向向量。

方向导数的准确表达式：
$$\frac{dw}{ds}{|}_{P_0,{\mathbf{u}}_0}=\nabla f\cdot \mathbf{u}$$
可以看出，方向导数是梯度向量在某一指定方向的投影，它一定小于梯度向量的大小，也就说明了函数沿梯度方向下降的最快（因为梯度包含了函数变化快慢的信息）。

2.5 偏导数的应用——求函数定义域内的最值

与单变量微积分中定义函数的导数来求最值一样（先算出让一阶导数为0的点，再计算其二阶导数来判断是最大值还是最小值）。定义多元函数的偏导数和微分形式也是为了方便求解函数的最值，了解函数的特征。但在这一节关注的是求多元函数在没有约束条件下的最值（自变量之间是无关的）

A. 二阶偏导数求最值的法则

1. 通过解方程组
   $$\{\begin{array}{l}{f}_x(x,y)=0\\ f_y(x,y)=0\end{array}$$
   找到临界点（Critical Point），有可能是最大值，最小值或者是鞍点（既不是最大值也不是最小值）
2. 令$A=f_{xx},B=f_{xy}=f_{yx},C=f_{yy}$，
   如果$AC-B^2=0$，不能确定临界点是哪一种最值，需要更多的信息；
   如果$AC-B^2<0$，则临界点是鞍点；
   如果$AC-B^2>0$且$A>0$，则临界点是最小值；
   如果$AC-B^2>0$且$A<0$，则临界点是最大值；

B. 简单验证——二元二次函数

二元二次函数的一般式为：$$w=a{x}^2+bxy+c{y}^2=y^2(a(\frac{x}{y}{)}^2+b(\frac{x}{y})+c)$$其中，$w_x=2ax+by$，$w_y=2cy+bx,A=w_{xx}=2a,B=w_{xy}=w_{yx}=b,C=w_{yy}=2c$

1. 如果$B^2-AC>0,A>0$，即 $b^2-4ac>0$且$a>0$，函数有最小值
2. 如果$B^2-AC>0,A<0$，即 $b^2-4ac>0$且$a<0$，函数有最大值
3. 如果$B^2-AC<0$，即 $b^2-4ac<0$，函数既有可能有最大值也有可能有最小值，也就是说函数有鞍点
4. 如果$B^2-AC=0$，即 $b^2-4ac=0$，函数$w=a(x+\frac{b}{2a}y{)}^2$有最小值。（但这里只是特殊情况）

更加一般化的证明以后需要了我再补上。

2.6 拉格朗日乘数法——解决约束条件下函数的最值问题

2.5节是用偏导数求解当函数自变量无关的情况下函数的最值，而有些时候，函数的自变量是相关的，即在函数$w=f(x,y,z)$满足约束条件$g(x,y,z)=C$的前提下，最大化或最小化函数$w$。

拉格朗日乘数法本质上是一种几何解法，让函数的等值面不断向约束条件靠近，最终两曲线相切，其梯度成倍数关系，即：
$$\nabla f=\lambda \nabla g$$

简单证明:

令$\mathbf{u}$为沿着约束条件$g(x,y,z)=C$ 的速度方向，那么函数$w=f(x,y,z)$取到最小值的时候它在这一方向上的方向导数必为0，即$$\frac{df}{ds}{|}_{\mathbf{u}}=\nabla f\cdot \mathbf{u}=0$$
即该函数的梯度向量与该约束条件的方向向量垂直，又因为约束条件函数的梯度$\nabla g$也垂直于该方向向量，所以$\nabla f=\lambda \nabla g$。

需要注意的是，$\lambda$算出来之后并不能确定是最大值还是最小值点，需要进行额外的判断，可以代入其他的数值进行确认。

2.7 涉及非独立变量多元函数的微分形式（Non-independent Variables）

非独立变量的问题依然是基于约束条件的，求含有非独立变量的函数$w=f(x,y,z)$在约束条件$z=g(x,y)$ 的条件下的偏导数$(\frac{\partial f}{\partial z}{)}_y$。

先明确符号表示，$(\frac{\partial f}{\partial x}{)}_y$为$y$固定下函数$f$对于$x$的偏导数。

常用步骤

方法1——分别写出约束条件和函数的微分形式

1. 将约束条件统一整理为$z=g(x,y)$的形式。
2. 写出函数$f$的微分形式，$df=f_{x}dx+f_{y}dy+f_{z}dz$，因为$y$是不变的，所以$y=C,dy=0$，从而可以得到$df=f_{x}dx+f_{z}dz$。
3. 结合第二步，写出约束条件的微分形式，$dg=f_{x}dx+f_{z}dz=0$，可以得到$dx=-\frac{g_z}{g_x}dz$
4. 带入函数$f$的微分形式可以得到，$df=(-f_x\frac{g_z}{g_x}+f_z)dz$，即$\frac{\partial f}{\partial z}{|}_y=(-f_x\frac{g_z}{g_x}+f_z)$

方法2——链式法则

1. 写出原函数的偏导数形式：
   $$\frac{\partial f}{\partial z}{|}_y=\frac{\partial f}{\partial x}\frac{\partial x}{\partial z}{|}_y+\frac{\partial f}{\partial y}\frac{\partial y}{\partial z}{|}_y+\frac{\partial f}{\partial z}\frac{\partial z}{\partial z}{|}_y$$$$\frac{\partial f}{\partial z}{|}_y=\frac{\partial f}{\partial x}\frac{\partial x}{\partial z}{|}_y+\frac{\partial f}{\partial z}$$
2. 写出约束条件下的偏导数形式：
   $$\frac{\partial g}{\partial z}{|}_y=\frac{\partial g}{\partial x}\frac{\partial x}{\partial z}{|}_y+\frac{\partial g}{\partial y}\frac{\partial y}{\partial z}{|}_y+\frac{\partial g}{\partial z}\frac{\partial z}{\partial z}{|}_y=g_x\frac{\partial x}{\partial z}{|}_y+g_z=0$$$$\frac{\partial g}{\partial z}{|}_y=g_x\frac{\partial x}{\partial z}{|}_y+g_z=0$$$$\frac{\partial g}{\partial z}{|}_y=-\frac{g_z}{g_x}$$

2.8 补充：矢量场和标量场概述——进入物理世界

标量场

标量场和矢场在物理学中非常重要。标量场就是由空间上某个点所含有的一些变量的信息转化为一个数字的函数，只有大小，没有方向（和标量的定义是一致的）常见的标量场有温度场（比如地球任意经纬度海拔高度下的一点的温度）；浓度场（液体中没一点的浓度）。

通常用等高线图来描述标量场（回顾梯度与等高线图的垂直关系）

矢量场

在矢量场中，空间里的每一个点都有大小和方向（和向量定义一致）。在第一章中，讲过向量函数，也就是矢量场的另一种表达方式。常见的矢量场有速度场（液体的流速），电磁场！！！！（电场和磁场，这是多变量微积分非常重要的应用！），重力场等