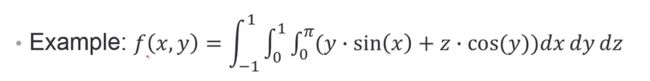台湾国立大学郭彦甫Matlab教程笔记（17）numerical integration

台湾国立大学郭彦甫Matlab教程笔记（17）numerical integration
数值积分
calculating the numerical value of a definite integral有限整数

quadrature method （求积分方法）

quadrature method （求积分方法）----approximating the integral by using a finite set of points 通过有限的点集，近似积分。.quadrature method 把x等分

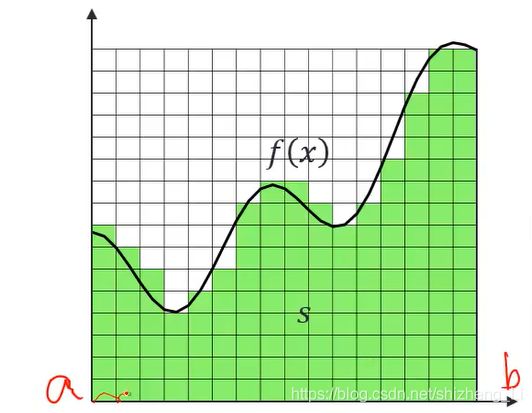
basic quadrature rules基本求积分方法

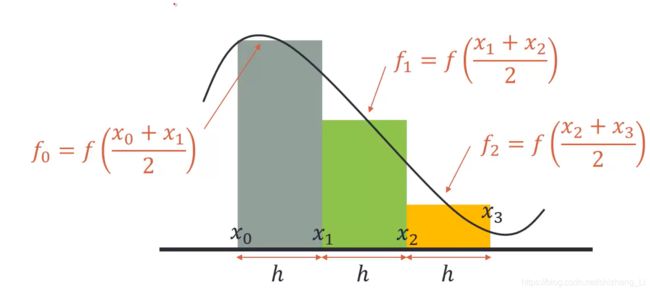
1.midpoint rule(zeroth-order approximation)
用矩形去做近似

2.trapezoid rule(first-order approximation)
用梯形去做近似

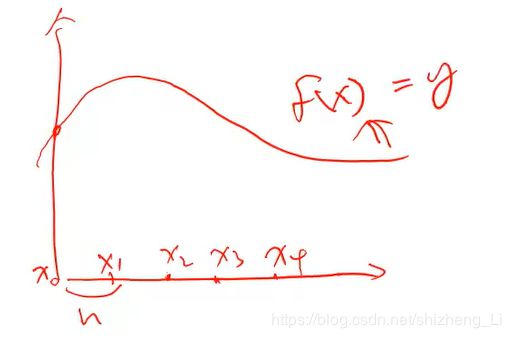
我们先来看 Midpoint Rule

对f(x)做积分，积分区间是x0~x3，把这个区间等分，每个等分距离是h
取每个等分小区间的中点处的函数值，来当作矩形的高

这个近似的过程如下图

小矩形的面积=底h乘以高f

实际上怎么用matlab做midpoint rule 呢？

midpoint rule using sum()
举例求解以下积分：

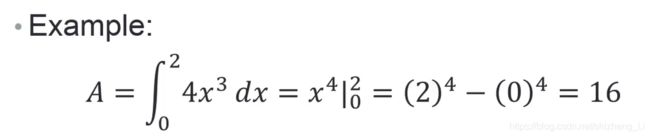
例程代码

h=0.05; x=0:h:2;
midpoint =(x(1:end-1)+x(2:end))./2;%找所有的中点
y=4*midpoint.^3;%被积函数，
s=sum(h*y)  %sum求得积分值

来理解中间这行代码的目的：
midpoint =(x(1:end-1)+x(2:end))./2;
由于midpoint rule 我们需要把区间中点值给f（x），所以需要计算出来中点值，midpoint,这句代码就是用来求中点值的。

执行结果：得到积分值是15.9950

how accurate is it?
积分值是16，用midpoint rule 计算得到是 15.9950，还算比较精准

how to improve the accuracy?
步长h减小

我们再来看 trapezoid rule

trapezoid 梯形，不规则四边形

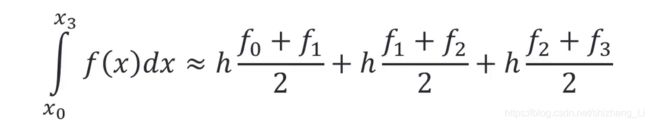
和上面的 midpoint rule 近似， 同样需要等分区间。这里每个小区间近似的函数值变掉了。
其中，h(f0+f1)/2表示的是梯形面积计算公式，（上底+下底）*高/2

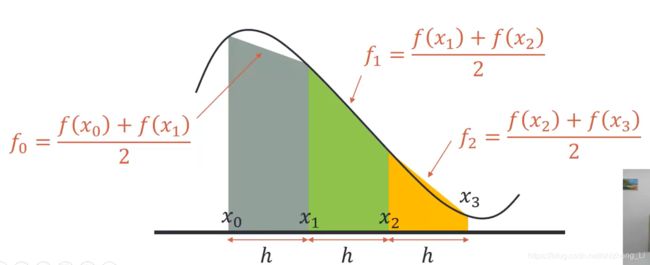
在matlab中如何使用trapezoid Rule 计算积分呢？
trapezoid rule using trapz()
同样的例题

例程代码：

h=0.05;%等分的小区间的长度
x=0:h:2;%等分x
y=4*x.^3;%被积函数
s=h*trapz(y)%在小区间上使用trapz计算梯形的面积

下图帮助理解：

计算结果：

还有另外一种使用形式

alternative:

h=0.05;
x=0:h:2;
y=4*x.^3;
trapezoid=(y(1:end-1)+y(2:end))/2;%求梯形的（上底+下底）/2
s=h*sum(trapezoid)

再多介绍一种second-order rule :1/3 Simpson’s

这个近似公式为：（很精准）（这里是用的两个小区间，所以只有三项，后面会看到更多的）

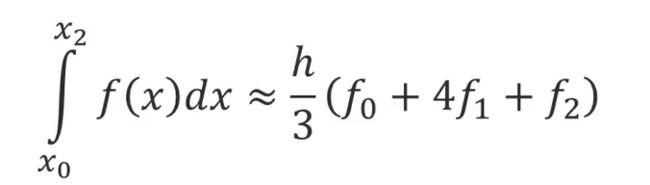
积分过程

Simpson’s rule
计算过程：
同样的例子：

程式码：

h=0.05;
x=0:h:2;
y=4*x.^3;
s=h/3*(y(1)+2*sum(y(3:2:end-2))+4*sum(y(2:2:end))+y(end))

运行结果：

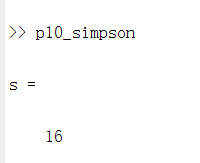
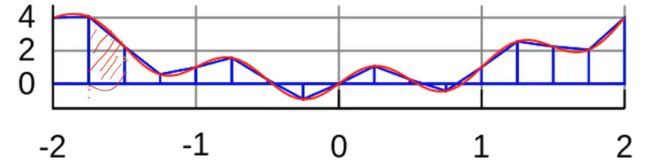
我们把三种方法做一个对比
comparison

用圆圈处的值做逼近

具体区别如下：

下面讲 函数句柄review of function handles(@)

a handle is a pointer to a function 函数句柄就是一个函数的指针
can be used to pass functions to other functions

通常，一个function 不能当作另外一个function 的input，函数句柄可以起到传递的作用
举例子：这里的input 是某一个function，比如sin

function [y]=xy_plot(input,x)
%xy_plot receives the handle of a function and plots that function of x
y=input(x);
plot(x,y,'r--');
xlabel('x');
ylabel('function(x)');
end

把上面这段代码储存成为.m文件，
然后尝试以下代码，去呼叫这个function
xy_plot(sin,0:0.01:2pi);
会报错，不能直接给这个function，需要给这个function 的指针pointer
正确的用法：
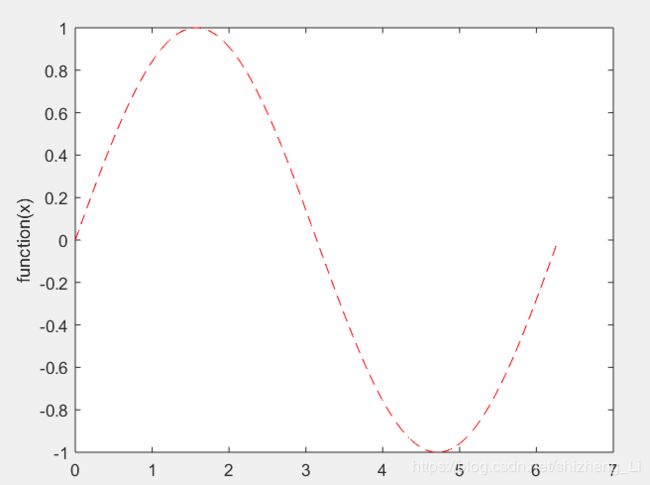
xy_plot(@sin,0:0.01:2pi);
运行结果：我们会发现，调用了这个sin函数，绘制了下图

我们看下一部分numerical integration :integral()

numerical integration on a function from using global adaptive quadrature and default error tolerances

例程：

y=@(x) 1./(x.^3-2*x-5);%让@(x) 指向被积函数
integral(y,0,2);

代码的解释：
integral(y,0,2);%y是被积函数，需要用函数句柄来表示，0和2是积分上下限

这个积分的结果：

思考，如果 要算sin（x）在[0,2]的积分怎么做？
同样的

y=@(x) sin(x);%让@句柄指向被积函数sin(x)
integral(y,0,2)

double and triple integrals两重或三重积分

二重积分使用函数：Integral2()
具体用法：integral(f,pi,2*pi,0,pi)%被积函数，和二重积分的两组积分限
计算下面的两重积分

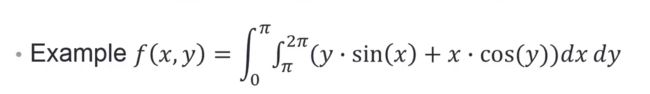
例程：

f = @(x,y) y.*sin(x)+x.*cos(y);
integral(f,pi,2*pi,0,pi)%被积函数，和二重积分的两组积分限

这个二重积分的计算结果：

三重积分用函数integral3()
具体用法：
integral3(f,0,pi,0,1,-1,1)%参数是被积函数，加上三对积分上下限

计算下列三重积分：

例程：

f=@(x,y,z) y.*sin(x)+z.*cos(y);
integral3(f,0,pi,0,1,-1,1)%参数是被积函数，加上三对积分上下限

上述积分的值为：

【总结一下】
本文记录了数值积分的一些用法。
介绍了三种求数值积分的方法：用矩形近似sum()函数，用梯形近似trapz()函数，还有Simpson方法。然后介绍了函数作为input的用法， 在此基础上讲解了数值积分integral()函数的用法：可以求解一重积分integral()、两重积分integral2()、三重积分integral3()函数等。