数据结构 常用排序

一、概述

1.排序的分类

1.1内部排序

• 插入排序：直接插入排序  希尔排序  折半插入排序（不常用）
• 交换排序：冒泡排序 快速排序
• 选择排序：简单选择排序  堆排序
• 归并排序
• 基数排序

1.2外部排序 

• 多路归并排序

常用的是内部排序，也是计算机类考研重点的考察对象。

2.各类算法比较

各类排序 算法性质

算法种类	最好情况 （时间）	平均情况（时间）	最坏情况（时间）	空间复杂度	是否稳定
直接插入排序	O(n)	O(n^2)	O(n^2)	O(1)	是
冒泡排序	O(n)	O(n^2)	O(n^2)	O(1)	是
简单选择排序	O(n^2)	O(n^2)	O(n^2)	O(1)	否
希尔排序				O(1)	否
快速排序	O(nlog2n)	O(nlog2n)	O(n^2)	O(log2n)	否
堆排序	O(nlog2n)	O(nlog2n)	O(nlog2n)	O(1)	否
2路归并排序	O(nlog2n)	O(nlog2n)	O(nlog2n)	O(n)	是
基数排序	O(d(n+r))	O(d(n+r))	O(d(n+r))	O(r)	是

从表中，不难得出以下结论：

1. 不稳定的算法有:简单选择排序 希尔排序 堆排序 快速排序
2. 排序趟数和初始序列无关的有 希尔排序 直接插入排序  简单选择排序 归并排序 基数排序
3. 元素比较次数和初始序列无关的有 简单选择排序 归并排序  基数排序
4. 直接插入排序在元素已经有序的情况下 时间复杂度最低为O(n)
5. 快速排序在元素有序或逆序的情况下 时间复杂度最高为O(n^2)

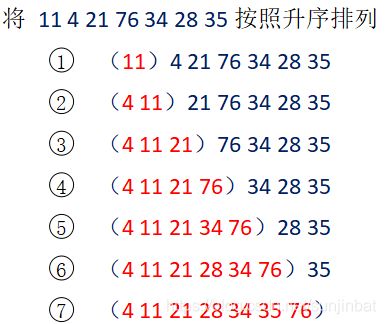
二、直接插入排序

def：对于给定的一组记录，初始时假定第一个记录自成一个有序的序列，其余的记录为无序序列；接着从第二个记录开始，按照记录的大小依次将当前处理的记录插入到其之前的有序序列中，直至最后一个记录插入到有序序列为止。

                                           

#include 
 
void InsertSort(int array[], int len)
{
    int i, j, temp;
 
    for(i = 1; i < len; i++)
    {
        temp = array[i];
 
        for(j = i - 1; j >= 0; j--)
        {
            if(temp < array[j])
            {
                array[j + 1] = array[j];
            }
            else
            {
                break;
            }
        }
        array[j + 1] = temp;
    }
}
 
int main()
{
    int i = 0;
    int a[] = {8, 2, 5, 3, 6, 7, 1, 9, 0};
    int length = sizeof(a) / sizeof(a[0]);
 
    InsertSort(a, length);
 
    for(i = 0; i < length; i++)
    {
        printf("%d ", a[i]);
    
    return 0;
}

三、希尔排序

def：希尔排序也称为“缩小增量排序”，基本原理是：首先将待排序的元素分为多个子序列，使得每个子序的元素个数相对较少，对各个子序分别进行直接插入排序，待整个待排序序列“基本有序后”，再对所有元素进行一次直接插入排序。 

                         

#include 
 
void ShellSort(int array[], int len)
{
    int i, j, temp, h;
 
    for(h = len / 2; h > 0; h = h / 2)
    {
        for(i = h; i < len; i++)
        {
            temp = array[i];
 
            for(j = i - h; j >= 0; j -= h)
            {
                if(temp < array[j])
                {
                    array[j + h] = array[j];
                }
                else
                {
                    break;
                }
            }
            array[j + h] = temp;
        }
    }
}
 
int main()
{
    int i = 0;
    int a[] = {8, 2, 5, 3, 6, 7, 1, 9, 0};
    int length = sizeof(a) / sizeof(a[0]);
 
    ShellSort(a, length);
 
    for(i = 0; i < length; i++)
    {
        printf("%d ", a[i]);
    }
 
    return 0;
}

四、 冒泡排序

嘿哈  这个太简单了 直接撸代码哈

#include 
 
void BubbleSort(int array[], int len)
{
	int i, j;
	int temp;
 
	for (i = 0; i < len -1; ++i)
	{
		for (j = len - 1; j > i; --j)
		{
			if (array[j] < array[j - 1])
			{
				temp = array[j];
				array[j] = array[j - 1];
				array[j - 1] = temp;
			}
		}
	}
}
 
int main()
{
	int i = 0;
	int a[] = {29, 18, 87, 56, 3, 27};
	int length = sizeof(a) / sizeof(a[0]);
 
	BubbleSort(a, length);
 
	for (i = 0; i < length; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
 
	return 0;
}

五、简单选择排序

def：对于给定的一组记录，经过第一轮比较后得到最小的记录，然后将记录与第一个记录的位置进行交换；接着对不包括第一个记录以外的其他记录进行第二轮排序，得到最小的记录并与第二个记录进行位置交换；重复该过程，直到进行比较的记录只有一个为止。

                                            

   

#include 
 
void SelectSort(int *num, int n)
{
    int i, j;
    int tmp = 0, min = 0;
 
    for(i = 0; i < n - 1; i++)
    {
        min = i;
 
        for(j = i + 1; j < n; j++)
        {
            if(num[j] < num[min])
            {
                min = j;
            }
        }
        if(min != i)
        {
            tmp = num[i];
            num[i] = num[min];
            num[min] = tmp;
        }
    }
}
 
int main()
{
    int i, len;
    int num[] = {4, 8, 2, 4, 0, 9, 1, 3, 5};
    len = sizeof(num) / sizeof(num[0]);
    
    SelectSort(num, len);
 
    for(i = 0; i < len; i++)
    {
        printf("%d ", num[i]);
    }
 
    return 0;
}

  六、快速排序

def：采用“分而治之”的思想，把大的拆分为小的，小的在拆分为更小的。对于一组给定的记录，通过一趟排序后，将原序列分为两部分，其中前部分的所有记录均比后部分的所有记录小，然后再依次对前后两部分的记录进行快速排序，递归该过程，直到序列中的所有记录均为有序为止。

#include 
 
int a[30], n;
 
void QuickSort(int left, int right)
{
    int i, j, tmp, tmp1;
    i = left;
    j = right;
 
    if(left >= right)
    {
        return;
    }
 
    while(i < j)
    {
        while(a[j] >= a[left] && i < j) //left作为参考值
        {
            j--;
        }
 
        while(a[i] <= a[left] && i < j)
        {
            i++;
        }
 
        if(i < j)
        {
            tmp = a[i];
            a[i] = a[j];
            a[j] = tmp;
        }
    }
 
    tmp1 = a[i];
    a[i] = a[left];
    a[left] = tmp1;
 
    QuickSort(left, i - 1);
    QuickSort(i + 1, right);
 
}
 
int main()
{
    int i;
 
    printf("Please input n:\n");
    scanf("%d", &n);
 
    printf("Please input number:\n");
    for(i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
    }
 
    QuickSort(1, n);
 
    for(i = 1; i <= n; i++)
    {
        printf("%d ", a[i]);
    }
 
    return 0;
}

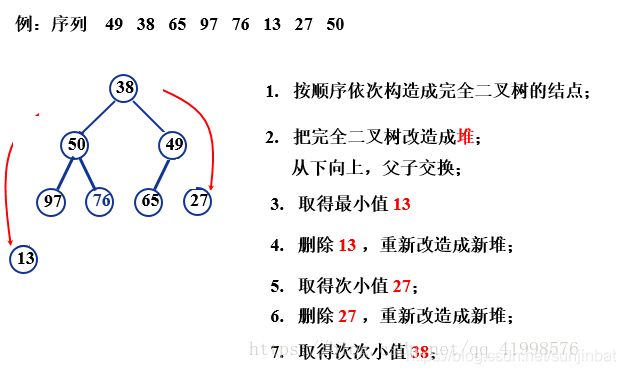
七、堆排序
   

 把这棵普通的完全二叉树改造成堆，便可获取最小值 ； 输出最小值 ；删除根结点，继续改造剩余树成堆，便可获取次小值 ；输出次小值 ；重复改造，输出次次小值、次次次小值，直至所有结点均输出，便得到一个排序 。

                        

堆增加一个节点的步骤是：放入最后一个节点 按照根节点到该节点的顺序进行组堆。

#include //适用于数据量大的时候(构建浪费时间)
 
void AdjustMinHeap(int *array, int pos, int len)
{
    int tmp, child;
 
    for(tmp = array[pos]; 2 * pos + 1 <= len; pos = child)
    {
        child = 2 * pos + 1;
        if(child < len && array[child] > array[child + 1])
        {
            child++;
        }
 
        if(array[child] < tmp)
        {
            array[pos] = array[child];
        }
 
        else
        {
            break;
        }
    }
    array[pos] = tmp;
}
 
void Swap(int *a, int *b)
{
    int temp;
    temp = *a;
    *a = *b;
    *b = temp;
}
 
void HeapSort(int *array, int len)
{
    int i;
 
    for(i = len/2 - 1; i >= 0; i--)
    {
        AdjustMinHeap(array, i, len - 1);
    }
 
    for(i = len - 1; i >= 0; i--)
    {
        Swap(&array[0], &array[i]);
        AdjustMinHeap(array, 0, i - 1);
    }
}
 
int main()
{
    int i;
    int array[] = {0, 13, 14, 1, 18, 27};
    int length = sizeof(array) / sizeof(array[0]);
 
    HeapSort(array, length);
 
    for(i = 0; i < length; i++)
    {
        printf("%d ", array[i]);
    }
 
    return 0;
}

八、归并排序

def：

利用递归与分治技术将数据序列划分为越来越小的半子表，再对半子表排序，最后再用递归步骤将排好序的半子表合并成为越来越大的有序序列。对于给定的一组记录，首先将两个相邻的长度为1的子序列进行归并，得到n/2个长度为2或者1的有序子序列，在将其两两归并，反复执行此过程，直到得到一个有序的序列为止。

                                    

#include 
#include 
 
void Merge(int array[], int start, int middle, int end)
{
	int i, j, k, n1, n2;
	
	n1 = middle - start + 1;              
	n2 = end - middle; 
 
	int *L = (int *)malloc(n1 * sizeof(int));
	int *R = (int *)malloc(n2 * sizeof(int));
 
	for (i = 0, k = start; i < n1; i++, k++)
	{
		L[i] = array[k];
	}
 
	for (i = 0, k = middle + 1; i < n2; i++, k++)
	{
		R[i] = array[k];
	}
 
	for (k = start, i = 0, j = 0; i < n1 && j < n2; k++)
	{
		if (L[i] < R[j])
		{
			array[k] = L[i];
			i++;
		}
		else
		{
			array[k] = R[j];
			j++;
		}
	}
 
	if (i < n1)
	{
		for (j = i; j < n1; j++, k++)
		{
			array[k] = L[j];
		}
	}
 
	if (j < n2)
	{
		for (i = j; i < n2; i++, k++)
		{
			array[k] = R[i];
		}
	}
}
 
void MergeSort(int array[], int start, int end)
{
	int middle;
	int i;
 
	if (start < end)
	{
		middle = (start + end) / 2;
		
		MergeSort(array, start, middle);
		MergeSort(array, middle + 1, end);
		Merge(array, start, middle, end);
	}
}
 
int main()
{
	int i = 0;
	int a[] = {49, 38, 65, 97, 76, 13, 27};
	int length = sizeof(a) / sizeof(a[0]);
 
	MergeSort(a, 0, length -1);
 
	for (i = 0 ; i < length; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
 
	return 0;
}

九、基数排序

步骤：

(1)分配，先从个位开始，根据位值(0-9)分别放到0~9号桶中（比如53,个位为3，则放入3号桶中）

(2)收集，再将放置在0~9号桶中的数据按顺序放到数组中 

                                  

#include 
 
int Getmax(int *a, int n)
{
        int i, max;
        max = a[0];
 
        for(i = 0; i < n; i++)
        {
                if(max < a[i])
                {
                        max = a[i];
                }
        }
        return max;
}
 
int countsort(int *a,int n, int exp)
{
        int output[n];
        int buckets[10] = {0};
        int i;
        for(i = 0; i < n; i++)
        {
                buckets[(a[i] / exp) % 10]++;
        }
 
        for(i = 1; i < n; i++)
        {
                buckets[i] += buckets[i - 1];
        }
 
        for(i = n - 1; i >= 0; i--)
        {
                output[buckets[(a[i] / exp) % 10] - 1] = a[i];
                buckets[(a[i] / exp) % 10]--;
        }
 
        for(i = 0; i < n; i++)
        {
                a[i] = output[i];
        }
        return 1;
}
 
 
 
int Radixsort(int *a, int n)
{
        int exp;
        int max = Getmax(a, n);
 
        for(exp = 1; (max / exp) > 0; exp *= 10 )
        {
                countsort(a,n,exp);
        }
        return 1;
 
}
 
int main()
{
        int i;
        int a[] = {278, 109, 63, 930, 589, 184, 505, 269, 8, 83};
        int len = sizeof(a) / sizeof(a[0]);
 
        Radixsort(a, len);
        for(i = 0; i < len; i++)
        {
                printf("%d ", a[i]);
        }
 
        return 0;
}