Gragh---Algorithm ---最小树形图

定义：

定根的最小树形图，就是给有向带权图中指定一个特殊的点root，求一棵以root为根的有向生成树T，并且T中所有边的总权值最小。

算法实现过程：（定根）

朱-刘算法的大概过程如下：参考：hqd_acm的专栏 +幻影阁

首先消除自环，显然自环不在最小树形图中。然后判定是否存在最小树形图，以根为起点DFS一遍即可。判断图的连通性，若不连通直接无解，否则一定有解。

之后进行以下步骤。

设cost为最小树形图总权值。
0.置cost=0。
1.求最短弧集合Ao （一条弧就是一条有向边）

除源点外，为所有其他节点Vi，找到一条以Vi为终点的边，把它加入到集合Ao中。

（加边的方法：所有点到Vi的边中权值最小的边即为该加入的边，记prev[vi]为该边的起点，mincost[vi]为该边的权值）

2.检查Ao中的边是否会形成有向圈，有则到步骤3，无则到步骤4。（可利用并查集）

（判断方法：利用prev数组，枚举为检查过的点作为搜索的起点，做类似DFS的操作）

3.将有向环缩成一个点。
假设环中的点有（Vk1，Vk2，… ，Vki）总共i个，用缩成的点叫Vk替代，则在压缩后的图中，其他所有不在环中点v到Vk的距离定义如下：
<1> gh[v][Vk]=min { gh[v][Vkj]-mincost[Vkj] } (1<=j<=i)而Vk到v的距离为
<2> gh[Vk][v]=min { gh[Vkj][v] }              (1<=j<=i)
同时注意更新prev[v]的值，即if(prev[v]==Vkj) prev[v]=Vk
另外cost=cost+mincost[Vkj] (1<=j<=i)

到步骤1.

<1>的理解：先假设环上所有边均选上，若下次选择某一条边进入该环，则可以断开进入点与进入点的前驱之间的边，即断开F[进入点]，因为之前已经把现有的最小值加到集合A0里面了，所以现在只要加上多出来的那一部分，也就是min{a[p,Vi]-f[Vi]}，所以等效为直接把a[p,node]赋值为min{a[p,Vi]-f[Vi]}，有点像增广的感觉，每次找到delta。

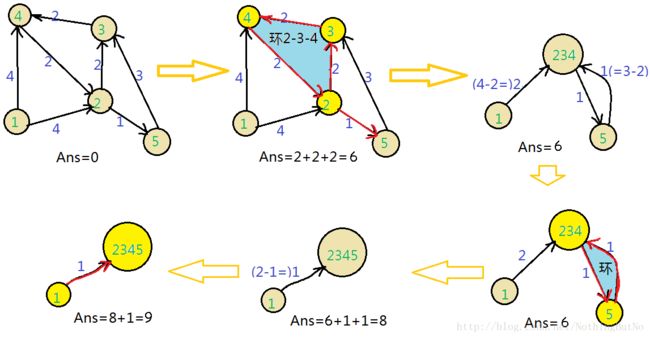
附一张图片加以理解：

4.cost加上Ao的权值和即为最小树形图总权值。

复杂度：有固定根

找环O(V)，收缩O(E)，总复杂度O(VE)。

模板：（POJ 3164 裸的最小树形图）

#include 
#include 
#include 
#include  
#include 
#include 
using namespace std;
const int inf=0x3f3f3f3f;
int n,m;
struct point
{
    int x,y;
}P[105];

struct Edge
{
    int u,v;
    double w;
}edge[10005];

int pre[105],color[105],mark[105];
int cnt_edge;
double in[105];

void AddEdge(int u,int v,double w)
{
    edge[cnt_edge].u=u;
    edge[cnt_edge].v=v;
    edge[cnt_edge].w=w;
    cnt_edge++;
}

double Cal(int x1, int y1,int x2, int y2)
{
    return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}

double zhuliu(int root,int n,int m)
{
    int i,j,u,v,cnt;
    double w;
    cnt=0;
    double res=0;

    while(1)
    {
        for(i=1;i<=n;i++)
            in[i]=inf;
        for(i=0;iw&&u!=v)
            {
                in[v]=w;
                pre[v]=u;
            }
        }
        for(i=1;i<=n;i++)
        {
            if(i!=root&&in[i]==inf)
            return -1;
        }
        memset(mark,0,sizeof(mark));
        memset(color,0,sizeof(color));
        mark[root]=1;
        in[root]=0;
        cnt=0;

        for(i=1;i<=n;i++)
        {
            res+=in[i];
            v=i;
            while(mark[v]!=i&&color[v]==0&&v!=root)
            {
                mark[v]=i;
                v=pre[v];
            }
            if(v!=root&&color[v]==0)
            {
                cnt++;
                for(u=pre[v];u!=v;u=pre[u])
                    color[u]=cnt;
                color[v]=cnt;
            }
        }

        if(cnt==0)
            break;
        for(i=1;i<=n;i++)
            if(color[i]==0)
                color[i]=++cnt;
        for(i=0;i