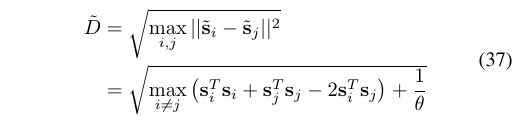文章目录
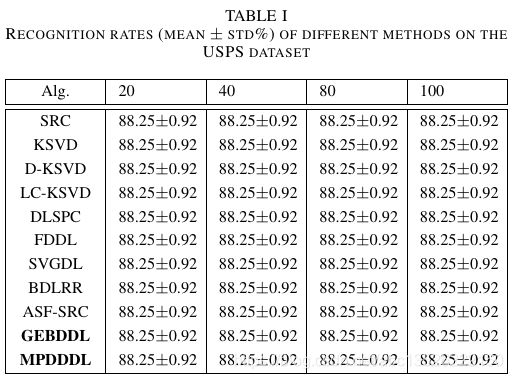
- 1. 表格1(单栏没有*)
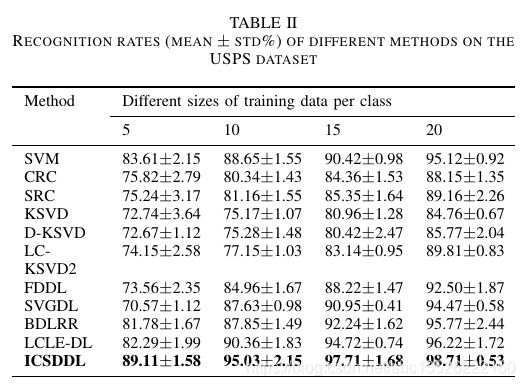
- 2. 表格2(单栏没有*)
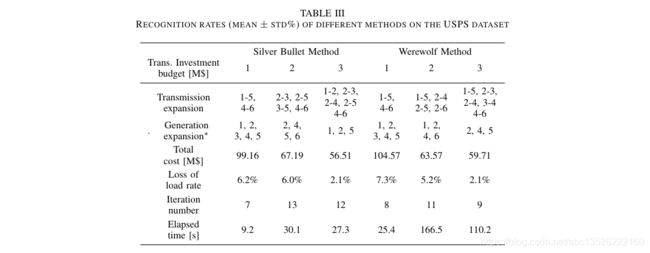
- 3. 表格双栏(双栏有*)
- 4. 图形(双栏有*)
- 5. 算法
- 6. 公式等号对齐
- 7. 补充算法
- 7.1. 方式1
- 7.1. 方式2
- 7.3. 方式3
- 参考文章
1. 表格1(单栏没有*)
\begin{table*}%[htbp] %htbp为位置控制
\caption{Recognition rates (mean $\pm$ std\%) of different methods on the USPS dataset}
\centering
\begin{tabular}{lllllll}
\toprule
&
\multicolumn{3}{c}{Silver Bullet Method} &
\multicolumn{3}{c}{Werewolf Method} \\
\InvB & \one & \two & \three & \one & \two & \three\\ % They are cells!!!! see the preambles to check the cell definitions!
\midrule
\TranExp & \TCo & \TCt & \TCth & \TCo & \TDt & \TDth \\[0.22cm].
\GenExp & \GCo & \GCt & \GCth & \GCo & \GDt & \GDth \\[0.22cm]
\TotalCost & \TcoC & \TctC & \TcthC & \TcoD & \TctD & \TcthD\\[0.22cm]
\LoL & \LoLoC & \LoLtC & \LoLthC & \LoLoD & \LoLtD & \LoLthD \\[0.22cm]
\IterNum & \InoC & \IntC & \InthC & \InoD & \IntD & \InthD\\[0.22cm]
\WallTime & \WtoC &\WttC &\WtthC & \WtoD &\WttD & \WtthD \\
\bottomrule
\end{tabular}
\end{table*}
2. 表格2(单栏没有*)
\begin{table}[!t]
\renewcommand{\arraystretch}{1.3}
\caption{Recognition rates (mean $\pm$ std\%) of different methods on the USPS dataset}
\label{table_example}
\centering
\begin{tabular}{|p{4.6em}|p{4.6em}|p{4.6em}|p{4.6em}|p{4.6em}|}
\hline
\centering
Alg.& 20 & 40 & 80 & 100 \\
\hline\hline
\centering
SRC & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 \\
\centering
KSVD & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 \\
\centering
D-KSVD & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 \\
\centering
LC-KSVD & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 \\
\centering
DLSPC & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 \\
\centering
FDDL & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 \\
\centering
SVGDL & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 \\
\centering
BDLRR & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 \\
\centering
ASF-SRC & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 \\
\centering
\bfseries GEBDDL & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 \\
\centering
\bfseries MPDDDL & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 & 88.25±0.92 \\
\hline
\end{tabular}
\end{table}
3. 表格双栏(双栏有*)
\begin{table*}%[htbp] %htbp为位置控制
\caption{Recognition rates (mean $\pm$ std\%) of different methods on the USPS dataset}
\centering
\begin{tabular}{lllllll}
\toprule
&
\multicolumn{3}{c}{Silver Bullet Method} &
\multicolumn{3}{c}{Werewolf Method} \\
\InvB & \one & \two & \three & \one & \two & \three\\ % They are cells!!!! see the preambles to check the cell definitions!
\midrule
\TranExp & \TCo & \TCt & \TCth & \TCo & \TDt & \TDth \\[0.22cm].
\GenExp & \GCo & \GCt & \GCth & \GCo & \GDt & \GDth \\[0.22cm]
\TotalCost & \TcoC & \TctC & \TcthC & \TcoD & \TctD & \TcthD\\[0.22cm]
\LoL & \LoLoC & \LoLtC & \LoLthC & \LoLoD & \LoLtD & \LoLthD \\[0.22cm]
\IterNum & \InoC & \IntC & \InthC & \InoD & \IntD & \InthD\\[0.22cm]
\WallTime & \WtoC &\WttC &\WtthC & \WtoD &\WttD & \WtthD \\
\bottomrule
\end{tabular}
\end{table*}
4. 图形(双栏有*)
\vspace{0.5cm}
\begin{figure*}
\begin{minipage}{0.5\textwidth} %% {0.18\textwidth}
\centerline{\includegraphics[width=0.85\textwidth]{loss.pdf}}
\centerline{\small{(a) Convergence comparison}}
\end{minipage}
\hfill
\begin{minipage}{0.5\textwidth} %% {0.90\textwidth}
\centerline{\includegraphics[width=0.85\textwidth]{acc.pdf}}
\centerline{\small{(b) Recognition rates versus iterations}}
\end{minipage}
\hfill
\caption{\small{Convergence comparison and recognition comparison versus iterations on the Extended Yale B dataset.}}
\label{fig:1}
\end{figure*}
\vspace{-1cm}

5. 算法
\usepackage{algorithm, algorithmicx} % For presenting algorithms
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Algorithm 2
\begin{algorithm}%[H]
% Exercise: Try to remove [H] and see what's gonna happen :P
% Answer: [H] means stick to the position.
\caption{Maximum pairwise distance guided discriminative dictionary learning (MPDDDL)}
\begin{algorithmic}
\State \textbf{Input:} The training samples $\mathcal{D}=\left\{\mathbf{x}_{i} | i=1, \dots, N\right\}$, parameters $\lambda_{1}, \lambda_{2}$ and $\theta$, the maximum number of iterations $T$, and the threshold $\sigma$ that denotes minimal difference in norm between dictionary $\mathbf{D}^{j}$ and $\mathbf{D}^{j+1}$.
\State \textbf{Output:} The learned dictionary matrix $\bf D$ and the hyperplane parameters $\{\hat{\mathbf{w}}_{c}, \hat{\bf{b}}_{c}) | c=1, \ldots, C\}$.
\State \textbf{Initialize:} the dictionary matrix $\bf D$ and the coding vector matrix $\bf S$.
\State \text{1:} \textbf{Repeat}
\State \text{2:} \qquad \textbf{Compute} $\widetilde{D}$ with (37);
\State \text{3:} \qquad \textbf{Compute} the partial derivatives (23);
\State \text{4:} \qquad \textbf{Update} $\{\hat{\mathbf{w}}_{c}, \hat{\bf{b}}_{c}) | c=1, \ldots, \}$ by employing a \\ \qquad \;\;\; gradient descent method;
\State \text{5:} \qquad \textbf{Compute} the partial derivatives (45);
\State \text{6:} \qquad \textbf{Update} $\bf S$ by employing a gradient descent method;
\State \text{7:} \qquad \textbf{Update} D with (33);
\State \text{8:} \textbf{Until} $\frac{\text{norm}\left(\mathbf{D}^{j+1}-\mathbf{D}^{j}\right)}{\text{norm}\left(\mathbf{D}^{j+1}\right)}<\sigma$ or $j>T$
\State \text{9:} \textbf{Return} the learned dictionary matrix $\bf D$ and the hyper-\\ \; \, plane parameters $\{\hat{\mathbf{w}}_{c}, \hat{\bf{b}}_{c}) | c=1,..., C\}$.
\end{algorithmic}
\end{algorithm}

6. 公式等号对齐
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 27
\begin{equation}
\begin{aligned}
\tilde D &= \sqrt {\mathop {\max }\limits_{i,j} ||{{{\tilde{\bf s}}}_i} - {{{\tilde{\bf s}}}_j}|{|^2}} {}\\
&=\sqrt {\mathop {\max }\limits_{i \ne j} \left( {{\bf{s}}_i^T{{\bf{s}}_i} + {\bf{s}}_j^T{{\bf{s}}_j} - 2{\bf{s}}_i^T{{\bf{s}}_j}} \right) + \frac{1}{\theta }}
\end{aligned}
\label{f2}
\end{equation}
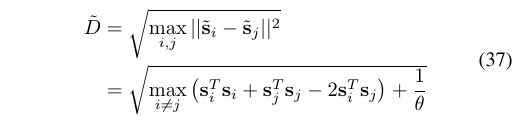
7. 补充算法
7.1. 方式1
\usepackage{algorithm, algorithmicx, algorithmic}
\begin{algorithm}[t]
\caption{Metric Learning Based on Intrinsic Structural Characteristic of Data} %算法的名字
{\bf Input:}
The training set ${\rm{\{ }}({{\bf{x}}_i},{y_i}){\rm{|}}i = 1,2,...,n{\rm{\} ,}}{{\bf{x}}_i} \in {{\bf{R}}^m}$\\
{\bf Output:}
The learned metric matrix $\bf M$.
\begin{algorithmic}[1]
\State \textbf{Initialize:} the dictionary matrix $\bf D$ and the coding matrix $\bf S$;
\Repeat
\While{the stopping criterion is not met}
\If{${l_i}({{\bf{w}}^T}{\bf{\tilde x}} + b) < 1$}
\State \textbf{Calculate} the partial derivatives $\frac{{\partial {\cal L}({\bf{w}},b)}}{{\partial \bf{w}}}$ and \hspace*{0.36in} $\frac{{\partial {\cal L}({\bf{w}},b)}}{{\partial b}}$ with (15);
\Else
\State \textbf{Calculate} the partial derivatives $\frac{{\partial {\cal L}({\bf{w}},b)}}{{\partial \bf{w}}}$ and \hspace*{0.36in} $\frac{{\partial {\cal L}({\bf{w}},b)}}{{\partial b}}$ with (17);
\EndIf
\State \textbf{end if}
\State \textbf{Update} $\bf{w}$ and $b$ by employing a gradient descent \hspace*{0.17in} method;
\State \textbf{Update} the metric matrix with (22) according to the \hspace*{0.22in}solution of (18);
\State $t = t + 1$;
\EndWhile
\Until{b}
\State \textbf{end while}
\State \Return The learned metric matrix $\bf M$.
\end{algorithmic}
\end{algorithm}

- 注意
- 关键字的大小写问题,否则会出现 Undefined control sequence.
- 控制流要前后对应。如果有 While,但没有 EndWhile,否则会出现 Some blocks are not closed。
7.1. 方式2
\usepackage[ruled]{algorithm2e}
\begin{algorithm}[H]
\caption{algorithm caption}%算法名字
\LinesNumbered %要求显示行号
\KwIn{input parameters A, B, C}%输入参数
\KwOut{output result}%输出
some description\; %\;用于换行
\For{condition}{
only if\;
\If{condition}{
1\;
}
}
\While{not at end of this document}{
if and else\;
\eIf{condition}{
1\;
}{
2\;
}
}
\ForEach{condition}{
\If{condition}{
1\;
}
}
\end{algorithm}

7.3. 方式3
\usepackage[ruled,vlined]{algorithm2e}

参考文章
- LaTeX算法表格(重要)
- LaTeX外部模板(IEEEtrans)初次套用经历
- LaTeX算法排版