二维矩阵的transpose函数:
不晓得该怎么起头,直接上干货。
transpose()简单来说,就相当于数学中的转置,在矩阵中,转置就是把行与列相互调换位置;
例如:随机生成一个三行五列的二维矩阵:
arr = np.arange(15).reshape((3, 5)) arr array([[ 0, 1, 2, 3, 4], [ 5, 6, 7, 8, 9], [10, 11, 12, 13, 14]]) >> arr.T
array([[ 0, 5, 10],
[ 1, 6, 11],
[ 2, 7, 12],
[ 3, 8, 13],
[ 4, 9, 14]])
reshape的作用是随机生成一个矩阵的行与列;
元素第0个位置表示0;第一个位置表示1,以此类推;总共是15个数;
然后arr.T相当于矩阵的转置;
transpose(X,Y)函数和矩阵的转置是一个意思,相当于行为X轴,列为Y轴,X轴和Y轴调换了位置;
X轴用0表示,Y轴用1表示;
例如:如果transport(1,0)表示行与列调换了位置;
>> arr.transpose(1, 0) array([[ 0, 5, 10], [ 1, 6, 11], [ 2, 7, 12], [ 3, 8, 13], [ 4, 9, 14]])
三维张量的transpose函数:
前面我们讲了二维矩阵的transpose函数其实是和矩阵的转置是一个概念;现在我们来讲一下三维张量;
三维张量顾名思义,它有三个维度;相当于有X轴,Y轴,Z轴;三个轴之间的相互转换;
同样,X轴用0表示,Y轴用1表示;Z轴用2来表示;
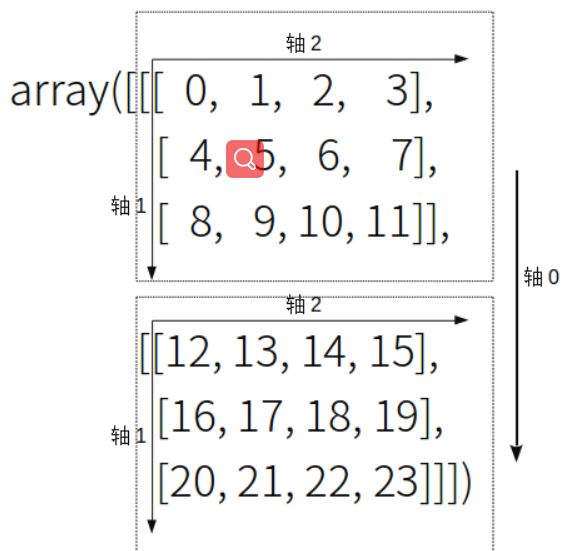
arr = np.arange(24).reshape((2, 3, 4)) arr array([[[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]], [[12, 13, 14, 15], [16, 17, 18, 19], [20, 21, 22, 23]]])
相当于把三维张量也做轴变换,具体操作如下图:
每个轴之间变换和表示也各不相同:
transpose(1,0,2)表示X轴与Y轴发生变换之后;
import numpy as np arr = np.arange(24).reshape((2,3,4)) vc = arr.transpose(1,0,2) print(vc) >>>结果 [[[ 0 1 2 3] [12 13 14 15]] [[ 4 5 6 7] [16 17 18 19]] [[ 8 9 10 11] [20 21 22 23]]]
transport(0,2,1):表示Y轴与Z轴发生轴变换之后;
import numpy as np arr = np.arange(24).reshape((2,3,4)) vc = arr.transpose(0,2,1) print(vc) [[[ 0 4 8] [ 1 5 9] [ 2 6 10] [ 3 7 11]] [[12 16 20] [13 17 21] [14 18 22] [15 19 23]]]
transport(2,1,0):表示X轴与Z轴发生轴变换之后;
import numpy as np arr = np.arange(24).reshape((2,3,4)) vc = arr.transpose(2,1,0) print(vc) [[[ 0 12] [ 4 16] [ 8 20]] [[ 1 13] [ 5 17] [ 9 21]] [[ 2 14] [ 6 18] [10 22]] [[ 3 15] [ 7 19] [11 23]]]
好了,到这里,差不多transport函数理解的也比较全面了,快去写写代码吧!